문제 접근하기
문제에 주어진 그래프의 종류와 제한 조건을 이해하느라 시간이 걸렸던 문제이다.
그래프의 종류는 총 3가지로, 도넛, 막대, 8자가 있다.
- 그래프의 종류 : 도넛, 막대, 8자
- 도넛 모양 그래프 - n 정점, n 간선
- 막대 모양 그래프 = n 정점, n-1 간선
- 8자 모양 그래프 = 2n+1 정점, 2n+2 간선
처음엔 무지성 그래프 순회로 풀려고 코드를 짜고 있었는데, 짜다보니 정점에 들어온 간선 개수를 확인해야 조건 분기로 그래프 종류를 체크할 수 있을 것 같았다.
그래서 map을 이용해 그래프를 처리하기로 방향을 바꾸었다.
정리하면 문제를 해결하기 위한 접근 순서는 아래와 같다.
- 그래프를 Map 객체로 만들어 나가고 들어오는 간선 개수 체크하기
- 그래프 종류를 파악하기 위한 노드 특징 파악하기
- 파악한 특징을 바탕으로 조건문 분기 처리하기
- answer 리스트에 답 넣기
그럼 이 순서에 따라 먼저 그래프를 Map으로 만들어보자.
그래프 Map으로 만들기 - 기본
const graph = edges.reduce((map, key) => {
if (!map.has(key[0])) {
map.set(key[0], [key[1]]);
} else {
map.get(key[0]).push(key[1]);
}
return map;
}, new Map());위 코드는 edges를 reduce함수를 이용해 매핑하는 코드이다. 초기화 칸에 new Map()을 넣어서 Map객체로 만들 것을 표기한다. 그리고 key마다 값이 있다면 get이후 push를 통해 value를 추가할 수 있다.
기본 코드를 이해했다면 이를 응용해서, 각 정점마다 [나가는 간선 개수, 받는 간선 개수]의 형태로 value를 저장하자.
그래프 Map으로 만들기 - 응용
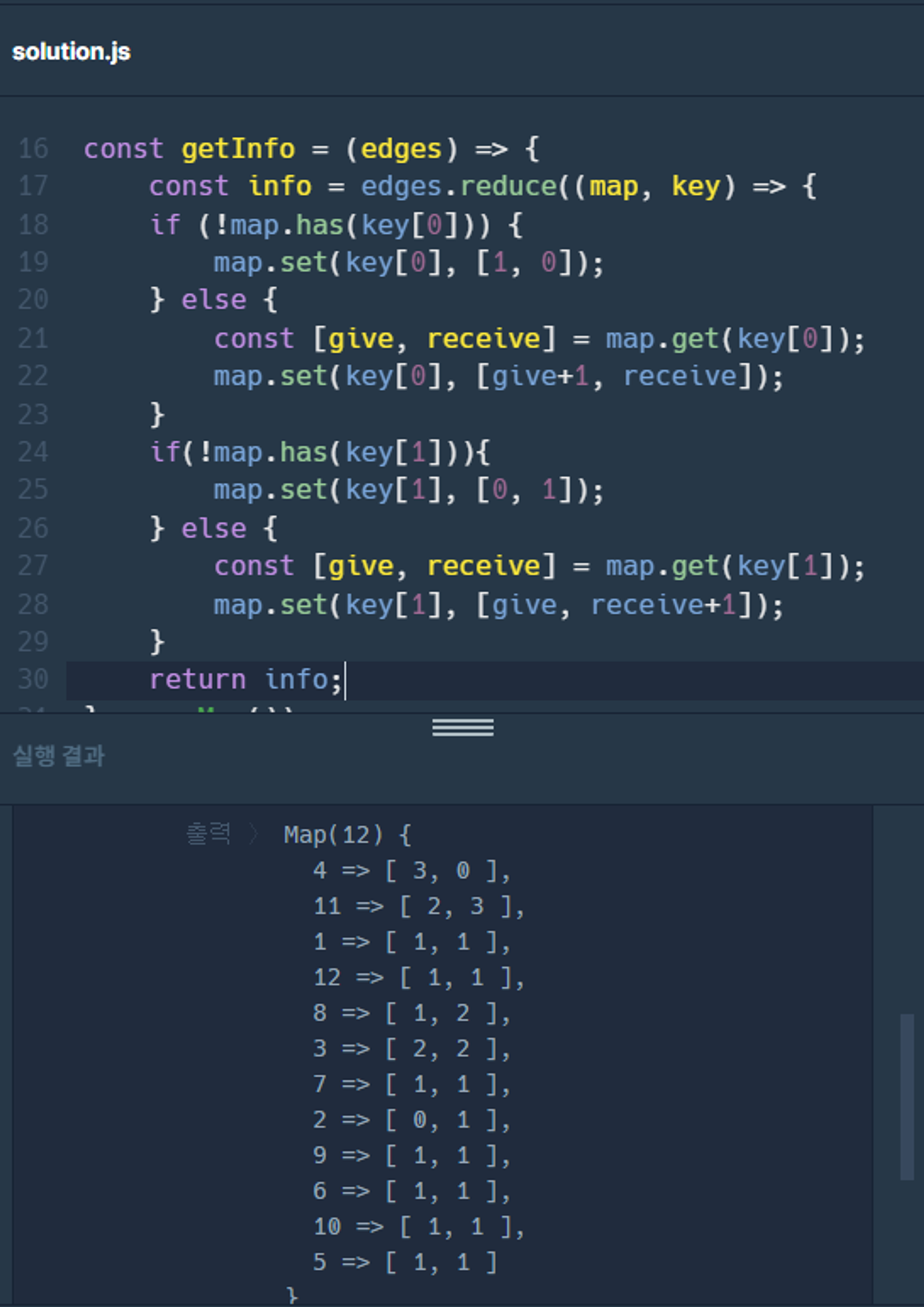
const getInfo = (edges) => {
const info = edges.reduce((map, key) => {
if (!map.has(key[0])) {
map.set(key[0], [1, 0]);
} else {
const [give, receive] = map.get(key[0]);
map.set(key[0], [give+1, receive]);
}
if(!map.has(key[1])){
map.set(key[1], [0, 1]);
} else {
const [give, receive] = map.get(key[1]);
map.set(key[1], [give, receive+1]);
}
return map;
}, new Map());
return info;
}
조건문으로 그래프 종류를 처리하기
문제에서 제시된 내용을 바탕으로 그래프 종류별로 edge 처리 조건을 구상해보자. 처음에 구상했던 처리해야할 그래프 종류, 정점 별 조건은 아래와 같다.
💡 실패한 제한 조건
- 도넛
: in edge == out edge || ( in ==1 && out == 0)
- 막대
: ( in edge == out edge -1 ) || (in edge == 0 || out edge == 0 )
- 8자
: ( in edge > out edge )
- 생성 정점
: ( in edge < out edge )
그런데 이렇게 처리할 경우, 입력 예제 2번에서 조건 처리가 터지게 된다. 그래서 다시 빠진 조건은 무엇인지 그래프를 천천히 살펴보고 가장 중요한 핵심을 찾아냈다.
이 그래프들과 무관한 정점을 하나 생성한 뒤, 각 도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프의 임의의 정점 하나로 향하는 간선들을 연결했습니다.
즉, 정리하면 생성 정점은 아래와 같은 조건을 충족하면서 생성됩니다.
1. 생성 정점은 기존 그래프의 연결 관계를 변경하지 않는다
2. 생성 정점은 기존 그래프 하나 당 하나의 연결 관계를 갖는다
이 조건에 더해, 기존 그래프의 개수가 최소 2개 이상이므로 in >= 2이고 out = 0 이면 생성 정점이 됨을 알 수 있다.
또한, 기존엔 모든 노드를 탐색해 조건을 충족하는지 살펴 봤지만 각 그래프를 이루는 정점 중 가장 특징이 두드러지는 노드만 찾아내도 그 그래프가 존재한다고 말할 수 있다.
- 막대 : 막대 그래프의 최상단에 위치한 노드는 간선에 대해 out = 0 이다.
- 8자 : 8자 그래프의 중앙점은 간선에 대해 in >= 2 && out >=2 를 만족한다.
- 생성 정점: 생성 정점은 기존 관계를 변경하지 않으므로 in == 0 && out >=2 를 만족한다.
마지막으로 도넛 그래프를 살펴보자.
- 도넛 : 사이클을 이룬다는 점 외에 정점 개수, 간선 개수로 판별할 수 있는 특징이 없다.
때문에 생성 정점이 기존 그래프마다 1개 간선을 갖는다는 아이디어를 이용해서 총 그래프 개수에서 막대, 8자 그래프 개수를 빼준다.
성공 코드 (js)
const getInfo = (edges) => {
const info = edges.reduce((map, key) => {
if (!map.has(key[0])) {
map.set(key[0], [1, 0]);
} else {
const [give, receive] = map.get(key[0]);
map.set(key[0], [give+1, receive]);
}
if(!map.has(key[1])){
map.set(key[1], [0, 1]);
} else {
const [give, receive] = map.get(key[1]);
map.set(key[1], [give, receive+1]);
}
return map;
}, new Map());
return info;
}
const chkInfo = (info) => {
const res = new Array(4).fill(0);
for(const [key, io] of info){
const [give, receive] = io;
if( 2 <= give && receive == 0) {
res[0] = key;
} else if(give == 0) {
//막대그래프 최상단은 give == 0
res[2]++;
} else if(give >= 2 && receive >= 2){
res[3]++;
}
}
// 도넛은 사이클이 이루어진다는 것 밖에 없기 때문에 개수 계산으로 판별할 수 없다.
// 생성 정점은 기존에 존재하던 모든 그래프에 간선을 하나 씩 연결한다.
// 따라서, 생성 정점의 간선 개수에서 막대, 8자 그래프 개수를 빼면 도넛 그래프 개수가 나온다.
res[1] = info.get(res[0])[0] - res[2] - res[3];
return res;
}
const solution = (edges) => {
const mapInfo = getInfo(edges);
const answer = chkInfo(mapInfo);
return answer;
}