[이분탐색] 입국심사

김아현·2023년 5월 8일

코딩테스트

목록 보기

9/26

프로그래머스 입국심사 파이썬 풀이

문제설명

n명이 입국심사를 위해 줄을 서서 기다리고 있습니다. 각 입국심사대에 있는 심사관마다 심사하는데 걸리는 시간은 다릅니다.

처음에 모든 심사대는 비어있습니다. 한 심사대에서는 동시에 한 명만 심사를 할 수 있습니다. 가장 앞에 서 있는 사람은 비어 있는 심사대로 가서 심사를 받을 수 있습니다. 하지만 더 빨리 끝나는 심사대가 있으면 기다렸다가 그곳으로 가서 심사를 받을 수도 있습니다.

모든 사람이 심사를 받는데 걸리는 시간을 최소로 하고 싶습니다.

입국심사를 기다리는 사람 수 n, 각 심사관이 한 명을 심사하는데 걸리는 시간이 담긴 배열 times가 매개변수로 주어질 때, 모든 사람이 심사를 받는데 걸리는 시간의 최솟값을 return 하도록 solution 함수를 작성해주세요.

제한 사항

입국심사를 기다리는 사람은 1명 이상 1,000,000,000명 이하입니다.

각 심사관이 한 명을 심사하는데 걸리는 시간은 1분 이상 1,000,000,000분 이하입니다.

심사관은 1명 이상 100,000명 이하입니다.

문제설명을 읽고 생각해보자. 심사 규칙은 심사 시작 시 무조건 두 사람은 그냥 들어가서 검사받고, 남은 사람들은 앞선 심사대가 비는 순대로 들어가서 검사받게 된다. 또, 제한 사항을 살펴보면 입국 심사를 기다리는 수와 심사 시간과 심사관의 범위가 매우 크게 주어져있다.

심사받는 사람의 수는 어떻게 계산할 수 있을까? 아마, 현재 총 심사시간을 심사관별 심사 시간으로 나눈 다음 합하면 알 수 있을 것이다.

이걸 제대로 살펴보지 않고 처음 코드를 작성할 때, 최소값에 min(times)* n // 2 # 첫 두 사람이 들어간 최소값 를 할당했다. 여기까진 심사대가 오직 두 곳인줄 알았다.. 다시 읽어보니, 심사관은 여럿일 수 있고 times의 길이도 2로 고정되지 않는다. 또한, times 배열이 정렬되어 있단 조건도 존재하지 않는다.

그래서 당연하게도 아래 1차 코드로 제출하면 모든 테케에서 실패한다.

1차 코드

# 무엇이 최소가 되는 케이스고 최대가 되는 케이스일까?
# 한곳에 다 뭉치면 최소값이 될 수 없음. 두 심사대 모두 들어갔을 때 최소라고 하자
# 반복문 안에서, 심사대에 선 사람의 수의 합 n이 될 때까지 심사를 진행
# ppl = 심사대에 서는 사람의 수 합
 
def solution(n, times):
    _low = min(times)* n // 2 # 첫 두 사람이 들어간 최소값
    _high = max(times) * n # 무지성 최대값
    while _low <= _high:
        ppl = 0 
        mid = (_low + _high)//2
        print(ppl, _low, mid, _high, 'before ---')
        for t in times:
            ppl += mid // t 
        if ppl < n :
            _low = mid + 1
        else : 
            _high = mid -1
        print(ppl, _low, mid, _high, 'after ---')
    return _low

1차 코드의 문제점 고치기

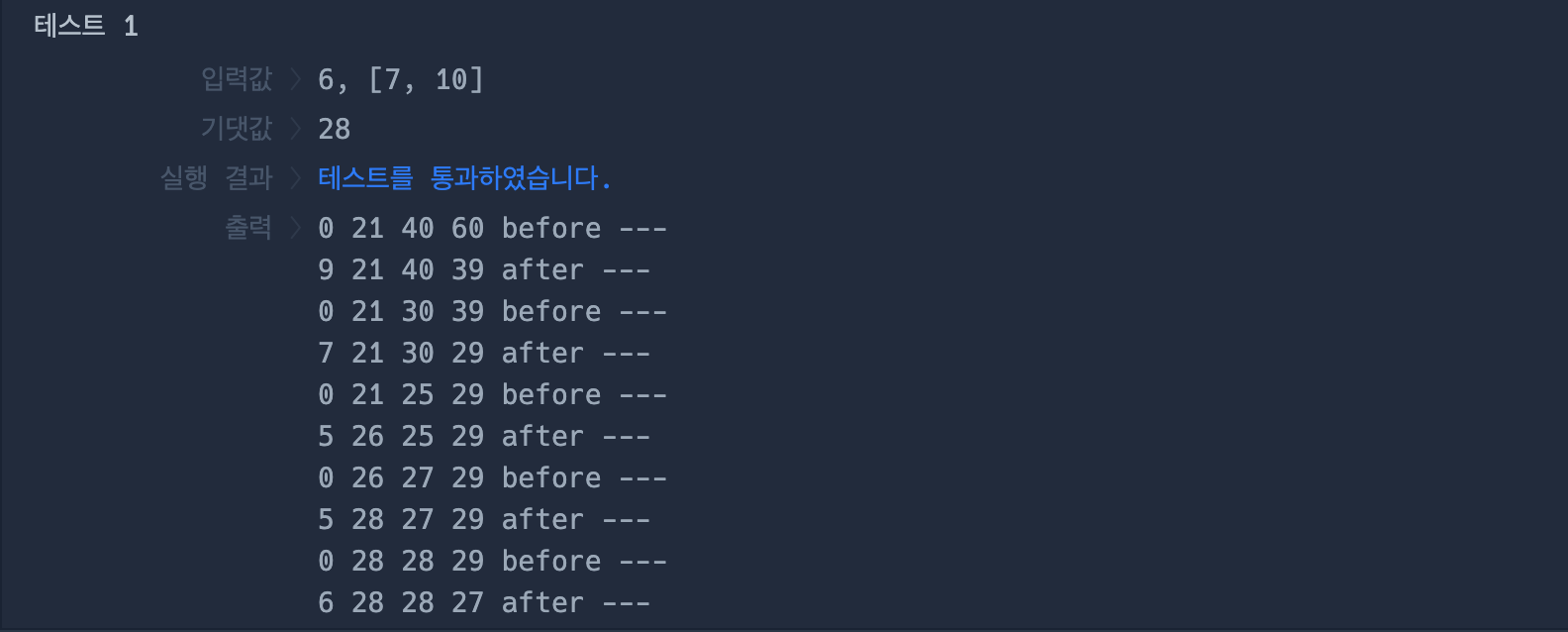
1차로 작성한 코드를 찍어보자. mid값을 기준으로 low와 high의 원소를 탐색하며 그 범위를 점차 좁혀가고 있는 모습을 볼 수 있다. 그리고 마지막에 두 범위가 뒤바뀌면 탐색이 종료된 것이므로 _low의 값을 리턴한다.

알고리즘은 이분 탐색에 알맞지만 _low의 초기값은 times와 n의 범위를 고려하며 시간복잡도를 줄일 수 있도록 1로 선언하자. 로직 확인이 끝난 출력문도 다 지운다.

2차 코드

def solution(n, times):
    _low = 1
    _high = max(times) * n # 무지성 최대값
    while _low <= _high:
        ppl = 0 
        mid = (_low + _high)//2
        for t in times:
            ppl += mid // t 
        if ppl < n :
            _low = mid + 1
        else : 
            _high = mid -1
    return _low