개똥벌레
출처 : 백준 #3020
| 시간 제한 | 메모리 제한 |
|---|---|
| 1초 | 128MB |
문제
개똥벌레 한 마리가 장애물(석순과 종유석)로 가득찬 동굴에 들어갔다. 동굴의 길이는 N미터이고, 높이는 H미터이다. (N은 짝수) 첫 번째 장애물은 항상 석순이고, 그 다음에는 종유석과 석순이 번갈아가면서 등장한다.
아래 그림은 길이가 14미터이고 높이가 5미터인 동굴이다. (예제 그림)
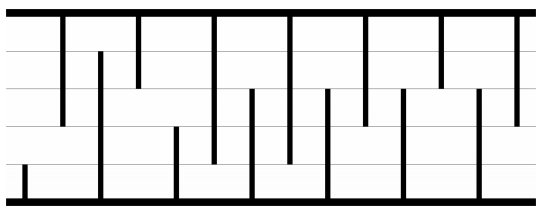
이 개똥벌레는 장애물을 피하지 않는다. 자신이 지나갈 구간을 정한 다음 일직선으로 지나가면서 만나는 모든 장애물을 파괴한다.
위의 그림에서 4번째 구간으로 개똥벌레가 날아간다면 파괴해야하는 장애물의 수는 총 여덟개이다. (4번째 구간은 길이가 3인 석순과 길이가 4인 석순의 중간지점을 말한다)
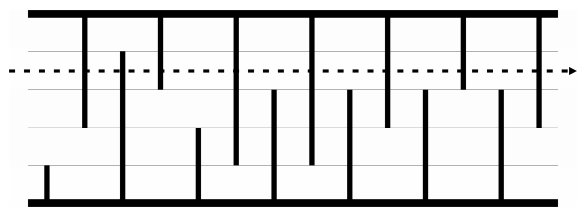
하지만, 첫 번째 구간이나 다섯 번째 구간으로 날아간다면 개똥벌레는 장애물 일곱개만 파괴하면 된다.
동굴의 크기와 높이, 모든 장애물의 크기가 주어진다. 이때, 개똥벌레가 파괴해야하는 장애물의 최솟값과 그러한 구간이 총 몇 개 있는지 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N과 H가 주어진다. N은 항상 짝수이다. (2 ≤ N ≤ 200,000, 2 ≤ H ≤ 500,000)
다음 N개 줄에는 장애물의 크기가 순서대로 주어진다. 장애물의 크기는 H보다 작은 양수이다.
출력
첫째 줄에 개똥벌레가 파괴해야 하는 장애물의 최솟값과 그러한 구간의 수를 공백으로 구분하여 출력한다.
입출력 예시
예제 입력 1
6 7
1
5
3
3
5
1
예제 출력 1
2 3
예제 입력 2
14 5
1
3
4
2
2
4
3
4
3
3
3
2
3
3
예제 출력 2
7 2
풀이
생각 및 풀이 설명
- upper bound(Binary Search)를 이용하여 해결하였다.
공통
- 우선 석순(mite)와 종유석(tite), 두 개의 리스트로 각각의 정보를 받아낸다.
- 이진 탐색을 위해 정렬한다. (이 부분 중요!!)
- 이진 탐색은 반드시 꼭 정렬이 된 상태에서 사용해야 한다.
- 아이디어를 생각해 낼 때 정렬을 해야하는 것을 생각한다면, 이진탐색을 쓸 문제인지 아닌지 파악할 수 있다.
- 종유석(tite)에 입력 값을 그대로 넣는 것이 아니라 높이에서 빼는 이유는 시작점을 0으로 맞추어 계산하기 위함이다.
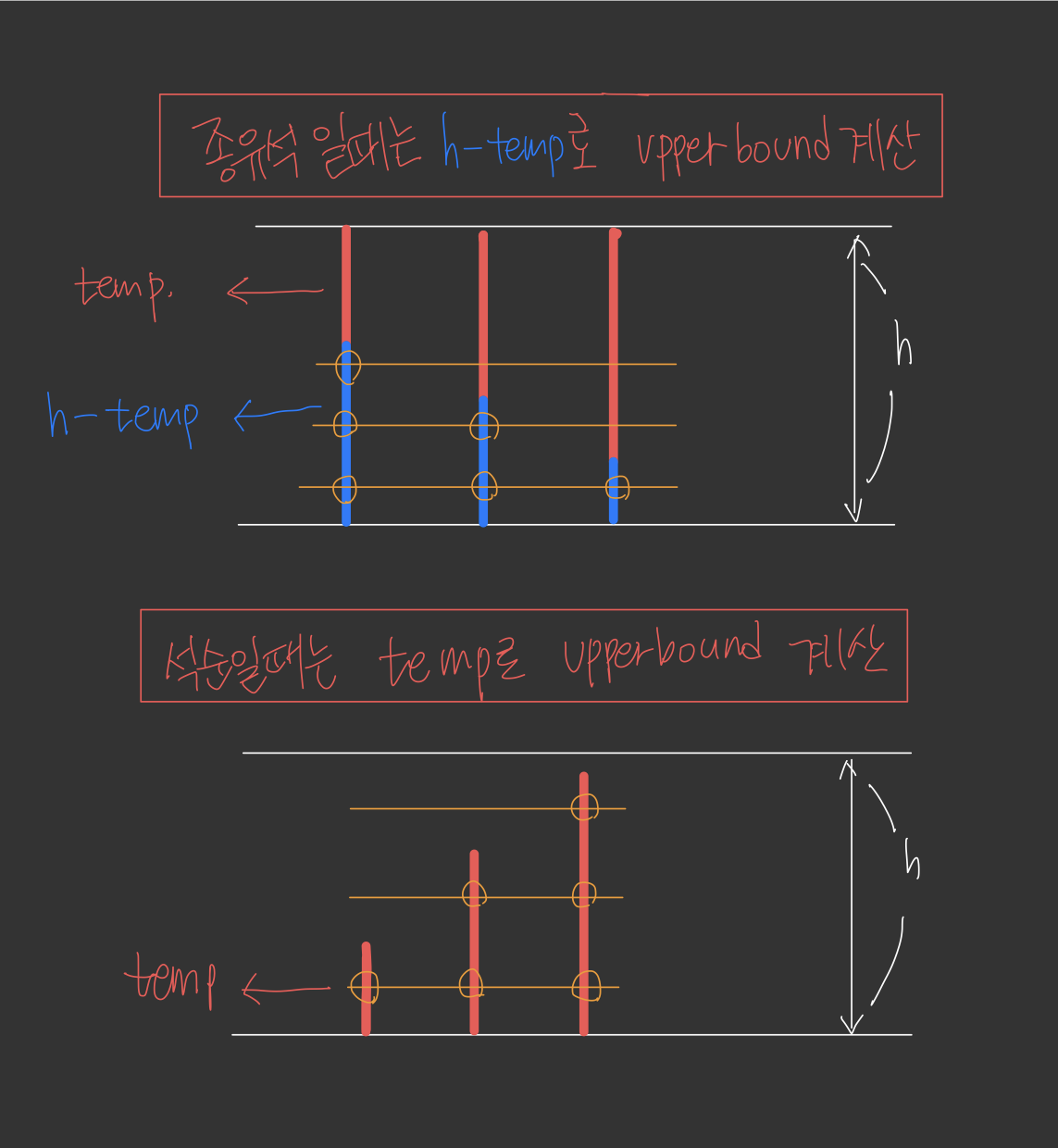
- 석순일 때는 temp와 만나기 직전의 인덱스를 반환한다.(r1)
- 따라서 n//2에서 뺀 값을 더해야 한다. (부숴야 하는 석순의 개수를 뽑아내야 하므로)
- 종유석일 때는 h-temp와 만나기 직전의 인덱스를 반환한다.(r2)
- 이때는 애초에 h-temp가 종유석이 없는 부분에 해당하기 때문에 그냥 반환한다. (부숴야하는 종유석의 개수를 뽑아내야 하므로)
- r1과 r2의 합을 그때 그때마다 최소값과 비교하고, 같다면
result += 1, 오히려 더 작다면, 최소값을 업데이트 해준다.
python code (upper bound)
# 백준 3020번 개똥벌레
from sys import stdin
input = stdin.readline
n, h = map(int, input().split())
mite, tite = [], [] # 석순, 종유석
def binarySearch_UpperBound(start, end, arr, target):
while start < end:
mid = (start+end)//2
if arr[mid] <= target:
start = mid + 1
else:
end = mid
return start
for i in range(n//2): # 입력 횟수 절반으로 줄임
mite.append(int(input())) # 석순
tite.append(h-int(input())) # 종유석 # [6, 4, 2]
mite.sort() # 석순 오름차순 정렬
tite.sort() # 종유석 오름차순 정렬
min_num, result = n, 0
for i in range(1, h+1):
r1 = n//2 - binarySearch_UpperBound(0, n//2, mite, i-1) # 닿은 면 체크
r2 = binarySearch_UpperBound(0, n//2, tite, i-1) # 닿지 않은 면 체크
total = r1 + r2 # (총 닿은 면 개수)
if min_num == total:
result += 1
elif min_num > total:
min_num = total
result = 1
print(min_num, result)