1. (log n) vs √n (밑이 2인 log)

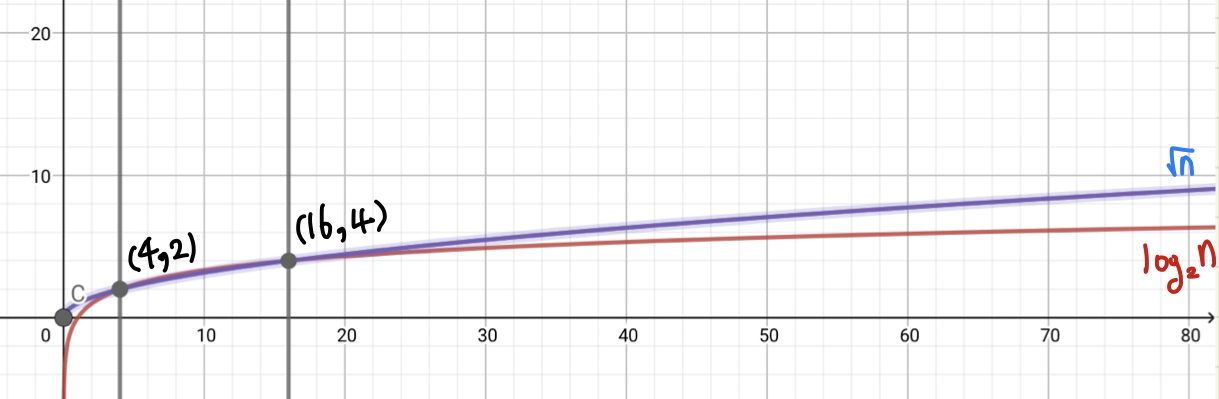
두 함수의 그래프를 직접 모눈종이에 나타내어 보았다.

점 (4,2)에서 처음으로 교점이 생기고 √n이 (log n)보다 낮다가,
점 (16, 4)에서 √n이 (log n)을 역전하고 더 가파른 기울기를 보인다.

따라서 n이 충분히 큰 값이라고 가정한다면, 시간 복잡도의 측면에서
O(log n)이 O(√n)보다 더 효율적이라고 할 수 있다.

n	log n	√n
4	2	2
4^2	4	4
4^3	6	8
4^10	20	1024
4^20	40	1048576

• 위의 표 결과만 숫자가 기하급수적으로 커졌을 때,
  log n이 얼마나 더 적은 숫자인지 나타내 준다.
  
  

---

---

2. 왜 알고리즘에서는 (log n)을 사용할 때, 밑이 2인 log 함수를 쓰는 것일까?

우선 알고리즘에 Θ(logn) (밑이 10인 로그) 시간이 소요된다고 한다고 가정하자.
사실 로그의 밑이 상수라면 점근적 표기법에서는 밑의 크기가 미치는 영향력이 작다고 볼 수 있다.

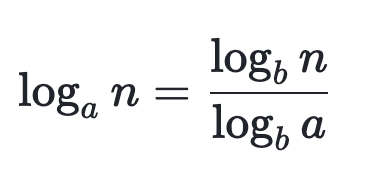
다음의 수학공식을 참고하면, 이는 모든 양수인 a,b,n에 대해서 성립하고 있다.
그러므로 만일 a,b가 상수라면, n을 포함하고 있는 (log(a) n)과 (log(b) n)은 (log(a) b)에 의해서만 달라지고 이는 무시할만한 상수의 값으로 볼 수 있다.

따라서 밑이 어떤 상수이든 간에 상관이 없다.

하지만 보통은 이진 검색을 할 때 Θ(logn) (밑이 2인 로그) 의 시간이 걸린다고 쓰는데, 이는 대부분의 컴퓨터 공학자들이 2의 제곱으로 수를 세는 것을 좋아하기 때문이란다. (믿거나 말거나)

---

출처 : https://ko.khanacademy.org/computing/computer-science/algorithms/asymptotic-notation/a/functions-in-asymptotic-notation