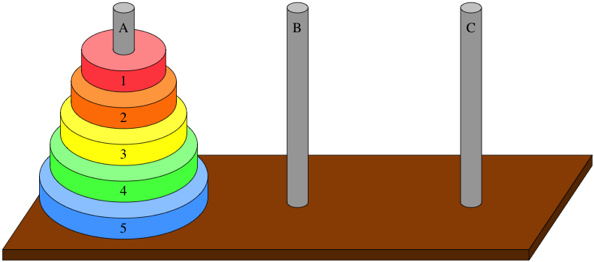
하노이의 탑 (Hanoi Tower) 문제 - Recursion

세 개의 막대기 1, 2, 3이 있고, 서로 다른 크기의 n개의 원반들이 막대기 1에 크기순서(위에서부터 아래로 크기가 증가)대로 놓여있다. 다음 규칙을 지키면서 막대기 1에 있는 모든 원반들을 막대기 3으로 옮겨라.

규칙 1 : 한 번에 막대기의 맨 위에 있는 한 장의 원반만을 다른 막대기 위로 옮길 수 있다.
규칙 2: 큰 원반은 절대로 작은 원반 위에 놓여질 수 없다.

알고리즘

• 단계 1) 막대기 1의 가장 큰 원반(가장 아래에 있는 원반)을 제외한 나머지 n-1개의 원반을 막대기 2로 옮긴다(막대기 3을 이용하여~)
• 단계 2) 막대기 1의 원반(가장 큰 원반)을 막대기 3으로 옮긴다.
• 단계 3) 막대기 2에 놓여 있는 n-1개의 원반을 막대기 3으로 옮긴다.(막대기 1을 이용~)

# recursion 이용
# 원반 n개를 source 번째 기둥에서 dest 번째 기둥으로 옮김 (feat. temp 번째 기둥을 보조하여.)
# source = 시작 기둥 / dest = 목표 기둥 / temp = 보조 기둥
def hanoiTower(n, source, dest, temp):
    if (n==1):
        print("Move a disk from peg %d to peg %d" % (source, dest))
    else:
        hanoiTower(n-1, source, temp, dest)     # 우선 보조 기둥(temp)에 마지막 원판을 제외하고 모두 옮긴다.
        print("Move a disk from peg %d to peg %d" % (source, dest)) # 마지막 원판을 시작 기둥에서 목표 기둥에 옮긴다.
        hanoiTower(n-1, temp, dest, source)     # line 8에서 보조기둥으로 모두 옮겼던 것들을 목표기둥으로 이동시킨다.

hanoiTower(3, 1, 3, 2)

하노이의 탑 알고리즘 수행시간 분석

T(n) : n장의 원반을 옮기는데 필요한 move 횟수
n = 1 인 경우 -> T(n) = 1
n > 1 인 경우 -> T(n) = 2T(n-1) + 1

T(n) = 2T(n-1) + 1 = 2[2T(n-2) + 1] + 1
     = 2^2T(n-2) + 2 + 1
     = 2^2[2T(n-3) + 1] + 2 + 1
     = 2^3T(n-3) + 2^2 + 2 + 1
     ...
     =2^kT(n-k) + 2^k-1 + ... + 2^2 + 2 + 1 = 2^kT(n-k) + 2^k + 1

n-k = 1, 즉 k = n - 1
2^(n-1)T(1) + 2^(n-1) -1
= 2^n - 1

따라서 O(2^n)의 시간 복잡도를 갖는다.
(수행시간 = 최악의 경우 수행시간 = 평균적인 경우 수행시간)