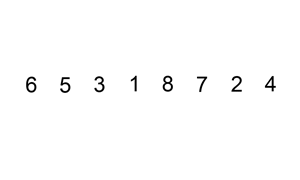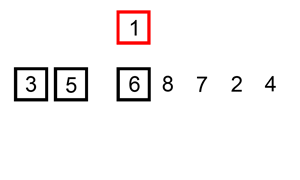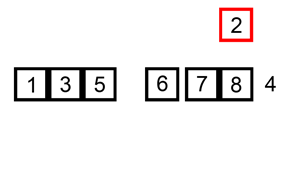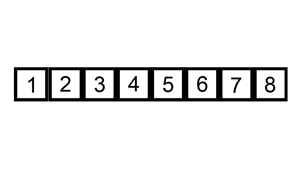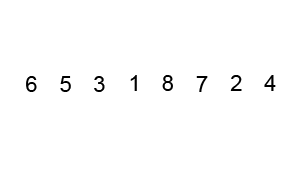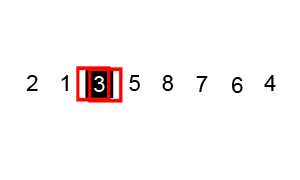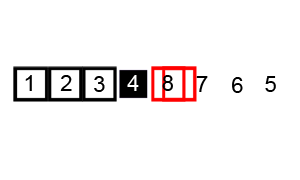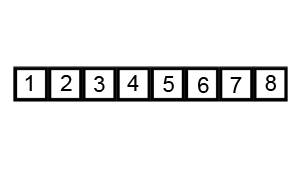[Python 알고리즘] # 정렬 알고리즘

- Bubble Sort (버블 정렬)

이웃한 두 값을 비교하여 모든 원소를 swap하는 작업을 반복하며 O(n^2)의 시간복잡도를 갖는다.

def swap(x, i, j):
    x[i], x[j] = x[j], x[i]

def bubbleSort(x):
    for size in reversed(range(len(x))):
        for i in range(size):
            if x[i] > x[i+1]:
                swap(x, i, i+1)

- Selection Sort(선택정렬)

각 회전마다 가장 작은 값을 찾아서 이를 맨 앞과 교환하는 방식을 가지고 있다.

앞에서부터 정렬해나가는 특성을 가지고 있으며 O(n^2) 시간복잡도를 가진다.

def swap(x, i, j):
    x[i], x[j] = x[j], x[i]

def selectionSort(x):
    for size in reversed(range(len(x))):
        max_i = 0
        for i in range(1, 1+size):
            if x[i] > x[max_i]:
                max_i = i
        swap(x, max_i, size)

- Insertion Sort (삽입정렬)

정렬되지 않은 값을 정렬된 배열 사이 올바른 자리에 데이터를 삽입하는 방식이다.

데이터의 양이 많아질수록 효율이 떨어지며 O(n^2) 시간복잡도를 갖는다.

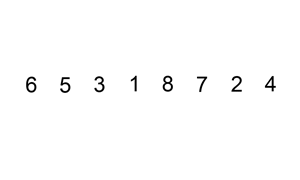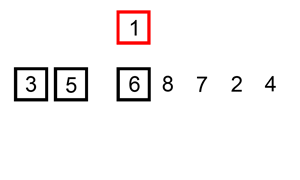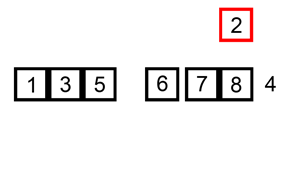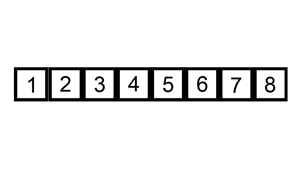
def insertionSort(x):
    for size in range(1, len(x)):
        val = x[size]
        i = size
        while i > 0 and x[i-1] > val:
            x[i] = x[i-1]
            i -= 1
        x[i] = val

- Merge Sort (병합 정렬)

두 부분으로 분할하는 과정을 재귀적으로 반복하고 작은 값부터 병합하는 분할 정복 알고리즘의 일종이다.

반으로 쪼개고 다시 합치는 과정에서 그룹을 만들어 정렬하므로 2n개의 공간이 필요하고 O(n log n)의 시간복잡도를 갖는다.

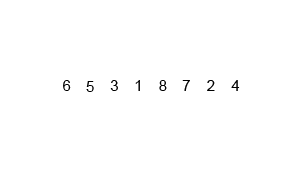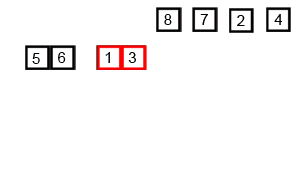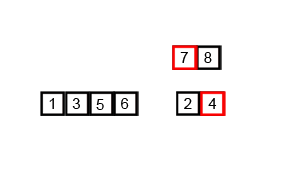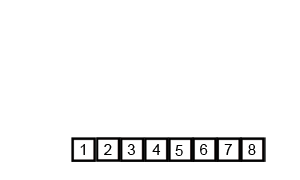
def mergeSort(x):
    if len(x) > 1:
        mid = len(x)//2
        lx, rx = x[:mid], x[mid:]
        mergeSort(lx)
        mergeSort(rx)

        li, ri, i = 0, 0, 0
        while li < len(lx) and ri < len(rx):
            if lx[li] < rx[ri]:
                x[i] = lx[li]
                li += 1
            else:
                x[i] = rx[ri]
                ri += 1
            i += 1
        x[i:] = lx[li:] if li != len(lx) else rx[ri:]

- Quick Sort (퀵 정렬)

병합 정렬과 마찬가지로 분할 정복 알고리즘의 일종이지만 추가적인 메모리 공간이 필요 없다.

Pivot(기준값)을 정하여 Pivot보다 작은 값은 앞으로, 큰 값을 뒤로 오도록 정렬하며 O(n log n) 시간복잡도를 갖는다.

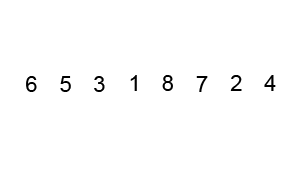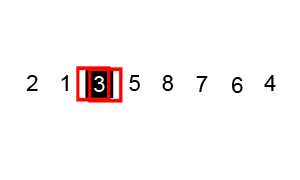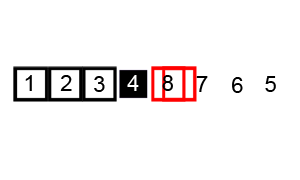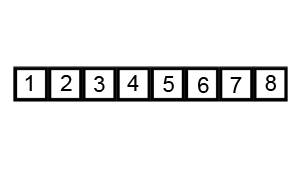
import random

a = random.sample(range(1, 10), 5) 
print(a) 
print('')
def quickSort(a, start, end):
    
    if start < end: 
        left = start 
        pivot = a[end] 
        for i in range(start, end): 
            if a[i] < pivot: 
                a[i], a[left] = a[left], a[i] 
                left += 1 
        a[left] , a[end] = a[end], a[left] 
        print(left)
        quickSort(a, start, left-1) 
        quickSort(a, left+1, end) 
quickSort(a, 0, len(a)-1)
print('')
print(a)

- 내장 정렬 메소드

특별한 경우가 아니라면 내장함수 sort를 통해 정렬을 할 수 있다.

import random
a = random.sample(range(1, 10), 5)

print(a.sort())