[백준] 1149. RGB거리

문제

RGB거리에는 집이 N개 있다. 거리는 선분으로 나타낼 수 있고, 1번 집부터 N번 집이 순서대로 있다.

집은 빨강, 초록, 파랑 중 하나의 색으로 칠해야 한다. 각각의 집을 빨강, 초록, 파랑으로 칠하는 비용이 주어졌을 때, 아래 규칙을 만족하면서 모든 집을 칠하는 비용의 최솟값을 구해보자.

• 1번 집의 색은 2번 집의 색과 같지 않아야 한다.
• N번 집의 색은 N-1번 집의 색과 같지 않아야 한다.
• i(2 ≤ i ≤ N-1)번 집의 색은 i-1번, i+1번 집의 색과 같지 않아야 한다.

입력

첫째 줄에 집의 수 N(2 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 각 집을 빨강, 초록, 파랑으로 칠하는 비용이 1번 집부터 한 줄에 하나씩 주어진다. 집을 칠하는 비용은 1,000보다 작거나 같은 자연수이다.

출력

첫째 줄에 모든 집을 칠하는 비용의 최솟값을 출력한다.

접근 방법

DP(Dynamic Programming, 동적 계획법)

DP라고 판단한 이유

n번째 집에 칠할 컬러를 판단하기 위해서는 n-1번째 집에서 색을 칠할 때 최소로 든 비용을 기반으로 해야한다.

• n번째 집에 색칠할 컬러는 n-1번째 집에 색칠한 컬러가 아니어야 한다.
• n번째 집에 색칠할 컬러는 n-1번째에서 칠할 때 가장 적은 비용이 드는 컬러여야 한다.

1. 1번째 집에는 R, G, B가 모두 올 수 있다.

2. 2번째 집에는 1번째 집에서 칠한 색깔을 칠할 수 없다.

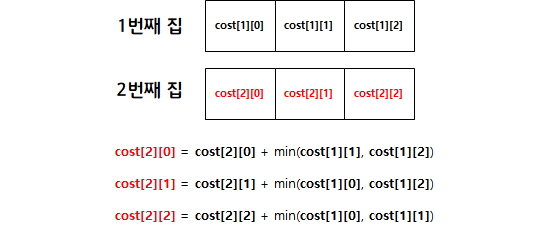
MinCost1은 2번째 집에 R 컬러를 칠하기 위해서는 1번째 집은 R 컬러를 칠해서 안되기 때문에 G, B 중 최소 비용을 가지는 컬러를 칠할 수 있도록 연산한다.

MinCost2와 MinCost3 역시 2번째 집에 각각 G 컬러와 B 컬러를 칠하기 위해서는 1번째 집이 같은 컬러를 칠해서는 안되기 때문에 각각 R/B, R/G 에서 최소 비용을 가지는 컬러를 칠할 수 있도록 연산한다.

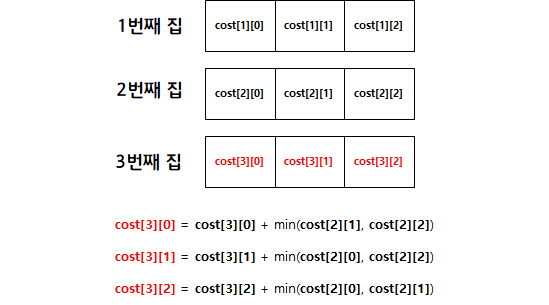
3. 3번째 집은 2번째 집에서 칠한 색깔을 칠할 수 없어야 하며 이제까지 최소로 비용을 치룬 집을 선택해야 한다.

JAVA 코드

2년 전에 이미 풀었었다..! 근데 엄청 오래 풀었다..

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		
		int[][] H = new int[n + 1][3];
		for(int i = 1; i <= n; i++) {
			H[i][0] = sc.nextInt();
			H[i][1] = sc.nextInt();
			H[i][2] = sc.nextInt();
			
			H[i][0] += Math.min(H[i - 1][1], H[i - 1][2]);
			H[i][1] += Math.min(H[i - 1][0], H[i - 1][2]);
			H[i][2] += Math.min(H[i - 1][0], H[i - 1][1]);
		}
		
		int max = H[n][0];
		for(int i = 1; i < 3; i++)
			max = max > H[n][i] ? H[n][i] : max;
		System.out.println(max);
	}
}