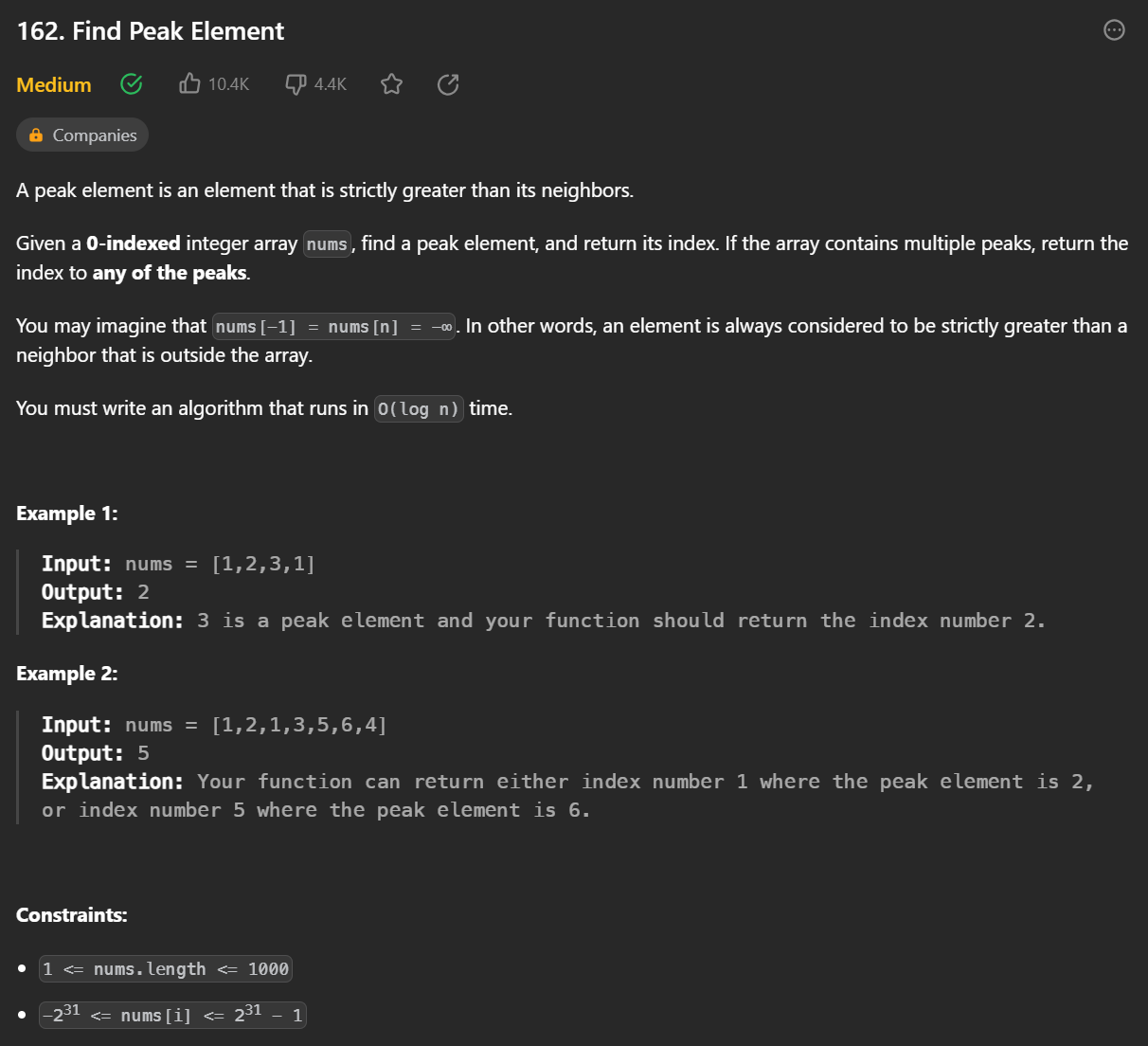
LeetCode 162 Find Peak Element

nayu1105·2023년 9월 3일

leetcode 알고리즘

LeetCode

목록 보기

23/28

LeetCode 162 Find Peak Element 풀러가기

문제

문제 분석

첫번째 시도(완전탐색)

문제를 보고 peek 지점이 나올때 까지 while문을 돌리는 코드를 짜려했는데, 초기 시작점이 아래로 내려가는지, 올라가는지 판별할 방법이 생각나지 않았다.

그래서 그냥 모든 index를 돌며, 이전값과 이후값을 비교했다.

억지로 length 가 1인 경우, 2인 경우를 넣으니 코드가 깔끔하지 않아보였다.

코드

class Solution {
    public int findPeakElement(int[] nums) {
       int index = 0;

       int distance = 0;
       int answer = 0;

       if(nums.length == 1) return 0;
       else if(nums.length == 2) return nums[0] > nums[1] ? 0 : 1;

       while(index < nums.length){
           int pre = index, before, next;
           if(index == 0){
               before = nums.length - 1;
               next = index + 1;
           }
           
           else if(index == nums.length - 1){
               before = index - 1;
               next = 0;
           }
           else {
               before = index - 1;
               next = index + 1;
           }

           if(nums[before] < nums[index] && nums[next] < nums[index]){
               int temp = Math.abs(nums[index] - Math.max(nums[before], nums[next]));
               if(temp > distance) answer = index;
           }

           index++;
       }
       
       return answer;


    }
}

결과 : 성공

Runtime

Memory

시간은 생각보다 남았다. 메모리도 좋지도, 나쁘지도 않은 그저 그랬던 것 같다.

그런데 코드가 깔끔하지 않아 다른 분들이 알아보기 어려워 할 거 같다.

다른 분의 코드 (이분탐색)

다른 방법을 알아보고자, 코드를 찾아보니 이분탐색으로 푸신 분이 있었다.

나는 distance를 주어서, peek 이면서, 그 양옆가 거리가 가장 차이나는 index를 찾았는데, 이 코드는 mid 기준으로 오른쪽에 peek가 있는지, 왼쪽에 peek가 있는지 찾아내는 코드였다.

~~문제를 다시 찾아보니, 가장 차이가 많이 나는 peek 를 찾는게 아니라 그냥 어떤 peek 든 return 하라고 되어있네..?~~

class Solution {
    public int findPeakElement(int[] arr) {
        int start = 0;
        int end = arr.length - 1;

        while(start < end){
            int mid = start + (end - start) / 2;
            if(arr[mid] > arr[mid + 1]){
                end = mid;
            }else{
                start = mid + 1;
            }
        }
        return start;
        
    }
}

결과 : 성공

Runtime

Memory

코드가 짧아지고, 비교문도 적어서 메모리가 더 작아질거라 기대했는데, 나와 비슷했다.

비교

완전 탐색은 O(N), 이분탐색은 O(logN)이기 때문에, 지금 테스트 케이스는 모르겠지만, 이후 더 많은 양의 케이스가 나올 시 이분탐색이 유리할 것 같다.

개선 코드

다른 분의 코드를 보고, 내가 문제를 잘 못 이해한 것을 알았다.

그래서 max distance를 찾는 코드를 빼고, peek 를 찾고 바로 리턴하는 구문을 짰다.

class Solution {
    public int findPeakElement(int[] nums) {
       int index = 0;

       int distance = 0;
       int answer = 0;

       if(nums.length == 1) return 0;
       else if(nums.length == 2) return nums[0] > nums[1] ? 0 : 1;

       while(index < nums.length){
           int pre = index, before, next;
           if(index == 0){
               before = nums.length - 1;
               next = index + 1;
           }
           
           else if(index == nums.length - 1){
               before = index - 1;
               next = 0;
           }
           else {
               before = index - 1;
               next = index + 1;
           }

           if(nums[before] < nums[index] && nums[next] < nums[index]){
               return index;
           }
           else index++;
       }
       
       return answer;


    }
}