LeetCode 167 Two Sum II - Input Array Is Sorted

nayu1105·2023년 8월 26일

leetcode 알고리즘

LeetCode

목록 보기

11/28

LeetCode 167 Two Sum II - Input Array Is Sorted 풀러가기

문제

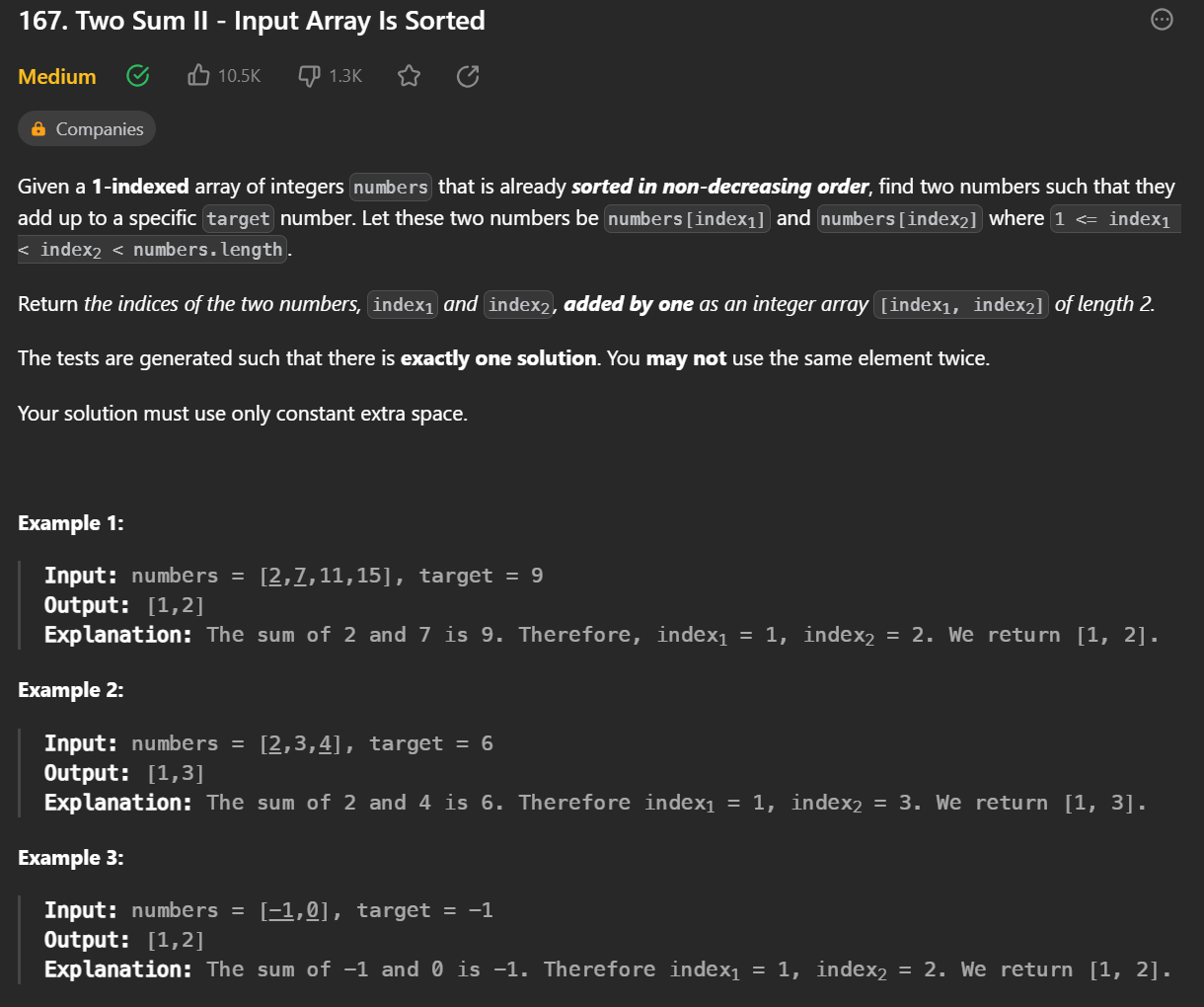
오름차순으로 정렬된 int 배열이 주어졌을 때 두개의 숫자를 더해서 target이 맞는 index를 각각 +1 한 int 배열을 반환한다.

예를 들어 numbers = [2, 7, 11, 15], target = 9 가 주어졌을 때, 2+7은 9가 될 수 있다.

2의 index = 0, 7의 index = 1 을 각각 1더하여, [1, 2]를 반환하면 된다.

문제에서 target이 될 수 있는 조합은 유일한 한가지만 주어진다.

문제 분석

첫번째 시도(소요시간 5분 : 시간복잡도 O(N) )

처음에는 이중 포문을 하면 모든 조합을 할 수 있으니 값을 찾을 수 있겠다고 생각했다.

그러나 이중 포문을 하면 시간복잡도가 O(N^2)이고, 문제에서 numbers의 최대 길이가 3 * 10^4 이라하여 너무 오래 걸릴 것 같았다.

number가 오름차순 정렬되어 있다는 힌트를 보고 다음과 같은 아이디어가 떠올랐다.

0번 인덱스와 맨 끝(number.length - 1) 인덱스의 합이 target보다 작다면 0번 인덱스는 정답의 배열에 들어갈 수 없었다.

다시 말해, 0번 인덱스와 어떤 값을 더했을 때 최대로 낼 수 있는 합이 맨 끝 인덱스와 더한 것인데, 이것이 target보다 작다면 0번 인덱스는 탐색할 필요가 없었다.
0번 인덱스와 맨 끝 인덱스를 더한 값이 target보다 작다면, 합이 target이 될 때까지 맨 끝 인덱스를 하나씩 줄여가면 됐다.

이 아이디어로 코드를 짰다.

코드

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        int index1 = 0;
        int index2 = numbers.length - 1;
        while(true){
            if(numbers[index1] + numbers[index2] == target) return new int[] {index1+1, index2+1};
            else if(numbers[index1] + numbers[index2] > target) index2 --;
            else index1 ++;
        }
    }
}

결과 : 성공

Runtime

Memory

비교 : 시간복잡도 O(N^2)

위 코드가 정말 좋은 성능을 내는가 비교해 보고 싶어서

처음 생각한 이중 포문을 이용해 코드를 구현해봤다.

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        for(int i=0; i<numbers.length; i++){
            for(int j=i+1; j<numbers.length; j++){
                if(numbers[i] + numbers[j] == target) return new int[] {i+1, j+1};
            }
        }
        return new int[] {};
    }
}