[백준] 24267번 알고리즘 수업 - 알고리즘의 수행 시간 6

NCOOKIE·2023년 3월 16일
Javaalgorithm백준
0

알고리즘

목록 보기
8/34
post-thumbnail

문제링크

들어가며

이번 문제는 코드는 간단하지만 수들의 패턴을 찾고 공식화 하는 것 때문에 애를 먹었다. 다른 블로그들에서는 코드에 사용하는 식만 딱 나와있고 그에 관한 설명은 충분히 되어있지 않거나 납득이 가지 않아, 예전에 배웠던 수학을 간신히 되새겨가며 설명해보았다.

참고로 이 포스팅의 작성자 분이 굉장히 똑똑하게 문제를 풀었다고 생각한다. 저런 식의 접근법은 생각치 못했던 것이라 언급해본다.

문제

아래 의사 코드에서 n이 주어졌을 때 수행횟수와 수행횟수의 다항식에서 가장 높은 차수를 출력하면 되는 간단한 문제이다. 

MenOfPassion(A[], n) {
    sum <- 0;
    for i <- 1 to n - 2
        for j <- i + 1 to n - 1
            for k <- j + 1 to n
                sum <- sum + A[i] × A[j] × A[k]; # 코드1
    return sum;
}

처음 코드를 봤을 때 직관적으로 이해가 가지 않아서 일단 돌려봤다.

public class Main {
    public static void main(String[] args) {
        int t = 7;
        int count = 0;
        
        for (int i = 1; i <= t - 2; i++) {
            for (int j = i + 1; j <= t - 1; j++) {
                for (int k = j + 1; k <= t; k++) {
                    System.out.printf("count=%02d \t|\t i : %d \t j : %d \t k : %d \n", ++count, i, j, k);
                }
            }
        }
    }
}
count=01 	|	 i : 1 	 j : 2 	 k : 3 
count=02 	|	 i : 1 	 j : 2 	 k : 4 
count=03 	|	 i : 1 	 j : 2 	 k : 5 
count=04 	|	 i : 1 	 j : 2 	 k : 6 
count=05 	|	 i : 1 	 j : 2 	 k : 7 
count=06 	|	 i : 1 	 j : 3 	 k : 4 
count=07 	|	 i : 1 	 j : 3 	 k : 5 
count=08 	|	 i : 1 	 j : 3 	 k : 6 
count=09 	|	 i : 1 	 j : 3 	 k : 7 
count=10 	|	 i : 1 	 j : 4 	 k : 5 
count=11 	|	 i : 1 	 j : 4 	 k : 6 
count=12 	|	 i : 1 	 j : 4 	 k : 7 
count=13 	|	 i : 1 	 j : 5 	 k : 6 
count=14 	|	 i : 1 	 j : 5 	 k : 7 
count=15 	|	 i : 1 	 j : 6 	 k : 7 
count=16 	|	 i : 2 	 j : 3 	 k : 4 
count=17 	|	 i : 2 	 j : 3 	 k : 5 
count=18 	|	 i : 2 	 j : 3 	 k : 6 
count=19 	|	 i : 2 	 j : 3 	 k : 7 
count=20 	|	 i : 2 	 j : 4 	 k : 5 
count=21 	|	 i : 2 	 j : 4 	 k : 6 
count=22 	|	 i : 2 	 j : 4 	 k : 7 
count=23 	|	 i : 2 	 j : 5 	 k : 6 
count=24 	|	 i : 2 	 j : 5 	 k : 7 
count=25 	|	 i : 2 	 j : 6 	 k : 7 
count=26 	|	 i : 3 	 j : 4 	 k : 5 
count=27 	|	 i : 3 	 j : 4 	 k : 6 
count=28 	|	 i : 3 	 j : 4 	 k : 7 
count=29 	|	 i : 3 	 j : 5 	 k : 6 
count=30 	|	 i : 3 	 j : 5 	 k : 7 
count=31 	|	 i : 3 	 j : 6 	 k : 7 
count=32 	|	 i : 4 	 j : 5 	 k : 6 
count=33 	|	 i : 4 	 j : 5 	 k : 7 
count=34 	|	 i : 4 	 j : 6 	 k : 7 
count=35 	|	 i : 5 	 j : 6 	 k : 7

이렇게 보니 규칙이 보인다. j를 기준으로 봤을 때 2가 5번, 3이 4번, 4가 3번, 5가 2번, 6이 1번, 그리고나서 3이 4번, 4가 3번... 이렇게 나열되어 있다. 이들의 합을 식으로 나타내면

5 + 4 + 3 + 2 + 1 +
4 + 3 + 2 + 1 +
3 + 2 + 1 +
2 + 1 +
1
= 35

알고리즘 문제를 풀다보면 많이 보던 패턴이다. 만약 n이 8이라면 n - 2인 6부터 시작하겠지. 그런데 생각해보니까 이전에는 공식을 찾기보다는 그냥 루프 돌려서 다 더했었다.

여기서부터 머리가 아파왔다. 이걸 어떻게 공식으로 만들지? 사람들은 뭘 근거로 n∗(n−1)∗(n−2)/6n * (n - 1) * (n - 2) / 6이라는 식을 내놓은거지???

풀이

우리가 구하려는게 뭔지 다시 정리해보자. n = 7일 때, 1 + 3 + 6 + 10 + 15를 구해야한다. 이들도 규칙을 가지고 있으니 수열이라고 할 수 있을 것이다. 그럼 먼저 이 수열의 n번째 수를 구하는 공식을 먼저 만들어보자.

등차수열의 합

위 수열의 n번째 값을 구하는건 간단하다. 1부터 n까지의 합을 구하면 된다. 그럼 다들 익숙한 가우스 선생님의 공식이 먼저 생각날 것이다. 만약 1부터 100까지의 합을 구하려면 맨 처음과 끝의 수를 더하고 거기에 100을 곱하고 2로 나누어준다.

이걸 좀 있어보이게 말하면 첫 항이 1, 공차가 1인 등차수열의 합이라고 할 수 있다. 가우스의 덧셈공식이 어떻게 나왔는지 간단하게 설명해보겠다.

등차수열의 합 SnS_n은 다음과 같이 표현할 수 있다.
Sn=1+2+3+...+(n−2)+(n−1)+nS_n = 1 + 2 + 3 + ... + (n - 2) + (n - 1) + n

그리고 이를 거꾸로 뒤집어보자.

Sn=n+(n−1)+(n−2)+...+3+2+1S_n = n + (n - 1) + (n - 2) + ... + 3 + 2 + 1

이 둘을 더하면

2Sn=(n+1)+(n+1)+...+(n+1)+(n+1)+(n+1)Sn=n(n+1)22S_n = (n + 1) + (n + 1) + ... + (n + 1) + (n + 1) + (n + 1)\\ S_n = \frac{n(n + 1)}{2}

그럼 이제 우리는 이러한 등차수열의 합들을 수열로 가지는 공식을 만들면 된다!

삼각수

자료를 찾다보니 알게 된 용어다.

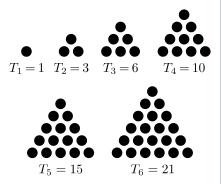
수학에서 삼각수(三角數, 영어: triangular number)는 1부터 시작하는 연속된 자연수의 합을 나타내는 수이다. (삼각수 - 위키백과, 우리 모두의 백과사전)

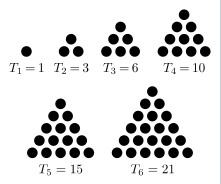
이럴수가. 위에서 구했던 등차수열의 합이 바로 이 삼각수를 구하는 식이었다. 따라서 우리는 이 삼각수들로 이루어져있는 수열 TnT_n의 합을 구하면 된다.

삼각수들의 합

삼각수들의 합을 시그마로 표현했을 때 아래와 같이 풀이할 수 있다.

∑k=1nk(k+1)2=∑k=1nk2+k2=12×(∑k2+∑k)=12×(n(n+1)(2n+1)6+n(n+1)2)=12×(2n(n+1)(2n+1)+3n(n+1)6)=12×(2n(n+1)(n+2)6)=n(n+1)(n+2)6\begin{aligned} \sum_{k=1}^{n}\frac{k(k + 1)}{2} &= \sum_{k=1}^{n}\frac{k^2 + k}{2} \\ &= \frac{1}{2} \times \left ( \sum k^2 + \sum k \right ) \\ &= \frac{1}{2} \times \left ( \frac{n(n + 1)(2n + 1)}{6} + \frac{n(n + 1)}{2} \right ) \\ &= \frac{1}{2} \times \left ( \frac{2n(n + 1)(2n + 1) + 3n(n + 1)}{6} \right ) \\ &= \frac{1}{2} \times \left ( \frac{2n(n + 1)(n + 2)}{6} \right ) \\ &= \frac{n(n + 1)(n + 2)}{6} \end{aligned}

자연수 거듭제곱의 합

위 풀이를 찾고 보면서 감탄하다가 이해가 되지 않는 부분이 있었다. 어째서 ∑k2\sum k^2가 6 분의 머시기로 변신을 했는가? 였다.

이에 대해서는 자연수 거듭제곱의 합을 구하는 공식과 유도가 따로 있는데, 여기서 설명하기보다는 링크로 대신하겠다. 사실 위의 식들 쓰면서 지쳐버렸다...

자연수 거듭제곱의 합

코드

드디어 코드를 써본다. 근데 별 내용은 없다. 위 공식에 n - 2를 대입해주고, 최고차항의 차수는 항상 3이기 때문에 그대로 출력하는 정도?

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        long n = Long.parseLong(br.readLine());

        System.out.println((n * (n - 1) * (n - 2)) / 6);
        System.out.println(3);
    }
}

참고링크

등차수열의 합, 등차수열의 합 공식

자연수 거듭제곱의 합 공식, 유도

삼각수 - 위키백과, 우리 모두의 백과사전

What is the summation of the series 1,3,6,10,15,....?

profile
NCOOKIE
일단 해보자
이전 포스트

[백준] 1929번 소수 구하기

다음 포스트

[SWEA][1859] 백만 장자 프로젝트

0개의 댓글

관련 채용 정보