[백준] 28116번 선택 정렬의 이동 거리

NCOOKIE·2024년 4월 28일
Javaalgorithm백준
0

알고리즘

목록 보기
10/34

문제 링크

들어가며

스터디에서 각자 진도에 맞는 알고리즘 문제를 풀기로 했는데 재밌어 보여서 고르게 되었다. 그러나 단순한 선택 정렬 알고리즘과는 다르게 생각보다 많은 시간을 투자했다. 아직 문제 풀이에 경험이 부족한 것 같다.

기능적인 구현 자체는 어렵지 않았지만 널리 알려진 선택 정렬 로직을 그대로 적용하면 시간 초과로 인해서 실패했다. 자바 대신 C로 작성해도 마찬가지였다. 게다가 대부분의 백준 문제는 검색하면 답과 풀이가 나오는데 이 문제 같은 경우에는 질문글만 1, 2개 나와서 많이 어려웠다.

문제를 풀면서 겪은 시행착오를 순서대로 적었다. 핵심 내용만 보려면 바로 마지막 파트인 정리 부분을 보면 된다.

문제

1부터 N까지 등장하는 정수가 한 번씩 등장하는 수열 A가 주어진다. 이 수열에서 선택 정렬 알고리즘을 수행할 때, 각 수의 이동거리를 출력해야 한다.

선택 정렬

  1. 주어진 리스트 중에 최소값을 찾는다.
  2. 그 값을 맨 앞에 위치한 값과 교체한다(패스(pass)).
  3. 맨 처음 위치를 뺀 나머지 리스트를 같은 방법으로 교체한다.

비교하는 것이 상수 시간에 이루어진다는 가정 아래, n개의 주어진 리스트를 이와 같은 방법으로 정렬하는 데에는 Θ(n2) 만큼의 시간이 걸린다.

선택 정렬은 알고리즘이 단순하며 사용할 수 있는 메모리가 제한적인 경우에 사용시 성능 상의 이점이 있다.

힌트

이 문제에서 핵심은 1부터 N까지의 자연수가 중복되지 않고 한 번씩은 꼭 등장한다는 것이다. 이 점 덕분에 각 숫자와 저장된 위치(인덱스)를 매칭하는 Map 또는 배열을 만들 수 있다.

풀이

버전 (1)

실패

처음에 아무 생각없이 선택 정렬을 구현해서 제출했던 코드다. 각 수의 이동거리를 가지고 있는 배열을 하나 만들어줬다. i번째 위치에 최소값이 위치 시킬 때마다 이동 거리를 저장하고 숫자의 위치를 스왑한다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
import java.util.Arrays;


public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;
        StringBuilder sb = new StringBuilder();

        int N = Integer.parseInt(br.readLine());
        int[] arr = new int[N];
        int[] answer = new int[N];

        st = new StringTokenizer(br.readLine());
        for (int i = 0; i < N; i++) {
            arr[i] = Integer.parseInt(st.nextToken());
        }

        for (int i = 0; i < N; i++) {
            int minIndex = i;
            
            for (int j = i; j < N; j++) {
                if (arr[j] < arr[minIndex]) {
                    minIndex = j;
                }
            }

            int distance = minIndex - i;
            answer[arr[i] - 1] += distance;
            answer[arr[minIndex] - 1] += distance;

            // swap
            int tmp = arr[i];
            arr[i] = arr[minIndex];
            arr[minIndex] = tmp;
        }

        for (int k = 0; k < N; k++) {
            sb.append(answer[k]).append(' ');
        }

        System.out.println(sb);
    }
}

수행 시간 초과

이 로직의 시간 복잡도는 O(n2n^2)이다. 그러나 제출 결과 시간 초과로 계속 실패했다. 불필요한 코드를 개선하거나 없애버려도 마찬가지였다.

이 문제의 경우 시간 제한이 5초라고 한다. 이 글에 따르면 아주아주 대충 잡아서 백준 기준 1초에 1억번 정도의 작업을 수행할 수 있다고 한다. 여기서 언어는 명시하지 않아 확실하지는 않지만 내가 사용하는 언어인 자바라면 몇 배는 더 뻥튀기 될 것으로 추측된다.

그럼 이를 실제 최악의 경우에 대입해보자. 입력값으로 데이터는 최대 5∗1055 * 10^5, 즉 50만개까지 들어올 수 있다. 이 데이터들을 받기 위해서 루프를 500,000번 받는다.

아래 선택 정렬을 구현한 중첩 for문의 경우 어림 잡아 수행 횟수가 (N * (N + 1)) / 2, 약 1200억번이다... 그렇다! 5초는 개뿔 대충 때려잡아도 20분은 걸린다. 거기다 JVM 위에서 돌아가는 Java인걸 감안하면...

결국 단순한 연산 횟수를 줄이거나 코드 한 두 줄에서 최적화해봤자 큰 의미는 없다는 뜻이다. 그래서 힌트를 얻기 위해 검색이나 질문 게시판 자료를 뒤져봤다.

버전 (2)

결정적인 힌트는 문제의 질문 게시판에서 얻을 수 있었다. (링크 1, 링크 2) 비록 완성된 코드는 아니라지만 정렬 부분의 for문이 한 개라는 점이 눈에 띄었다.

위 코드들의 핵심은 저장될 숫자를 key로 가지고, 그 숫자가 저장되는 위치, 인덱스를 value로 가지는 딕셔너리 또는 Map을 만든 것이다. 어차피 입력 데이터는 1부터 N까지의 모든 정수가 들어오기 때문에 현재 루프의 인덱스에 어떤 값이 들어와야 하는지 알 수 있다. 그리고 그 인덱스는 key-value 구조의 Map에서 바로 알 수 있다.

이를 적용한 코드는 아래와 같다. (수행 시간 1200ms)

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.HashMap;
import java.util.Map;
import java.util.StringTokenizer;


public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;
        StringBuilder sb = new StringBuilder();

        int N = Integer.parseInt(br.readLine());
        // int[] arr = new int[N];

        // key(수열의 값)과 value(값이 저장된 인덱스)로 이루어진 맵 자료구조
        // 수열의 값이 몇 번째 인덱스에 있는지 알 수 있음
        Map<Integer,Integer> idxMap = new HashMap<>();

        // 수열 A를 저장하고 있는 배열
        int[] numArr = new int[N + 1];

        // 각 숫자의 이동거리를 저장하는 배열
        int[] answer = new int[N + 1];

        st = new StringTokenizer(br.readLine());
        for (int i = 1; i <= N; i++) {
            int num = Integer.parseInt(st.nextToken());
            idxMap.put(num, i);
            numArr[i] = num;
        }

        // 수열 A는 1부터 N까지 있으므로 1부터 시작
        for (int i = 1; i <= N; i++) {
            // 현재 최소값이 와야하는 위치의 값이 최소값이 아닌 경우
            if (numArr[i] != i) {
                // 정렬되지 않은 부분의 최소값이 저장된 위치
                int minIndex = idxMap.get(i);

                // 최소값이 저장된 위치와 현재 정렬하려는 위치 간의 거리
                int distance = minIndex - i;

                // 이동한 값들의 숫자에 거리 추가
                answer[numArr[i]] += distance;
                answer[numArr[minIndex]] += distance;

                // 맵의 key-value 스왑
                int tmp = idxMap.get(i);
                idxMap.put(i, idxMap.get(numArr[i]));
                idxMap.put(numArr[i], tmp);

                tmp = numArr[i];
                numArr[i] = numArr[minIndex];
                numArr[minIndex] = tmp;
            }

            sb.append(answer[i]).append(' ');
        }

        System.out.println(sb);
    }
}

입력 데이터로 {1, 3, 5, 2, 4}가 들어온다고 할 때, idxMap은 아래와 같이 저장될 것이다. 그리고 numArr에는 수열 A가 numArr[1]부터 그대로 저장될 것이다.

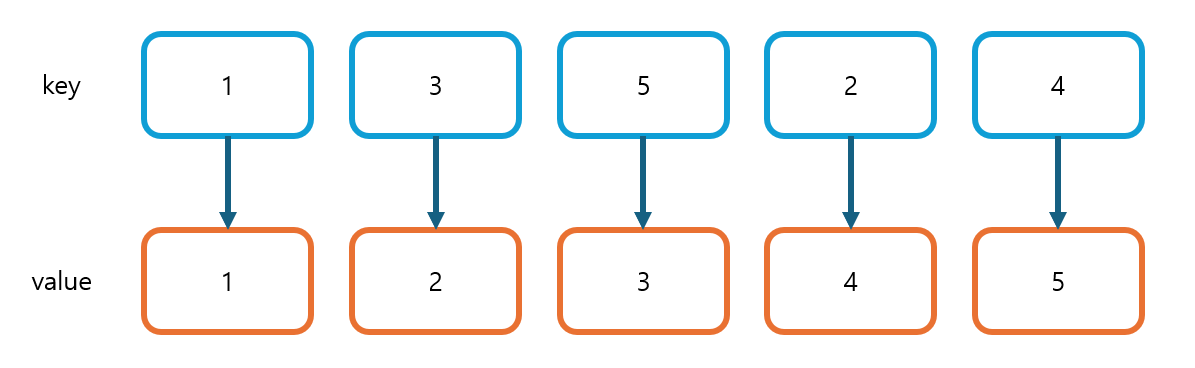
이제 선택 정렬 부분을 구현한 중첩 for문 쪽을 살펴보자.

첫 번째 루프는 numArr[1]와 i가 모두 1이기 때문에 아무 것도 하지 않는다.

두 번째 루프에서는 numArr[2]와 i가 각각 3, 2이므로 다르다. 현재 1까지는 정렬된 상태이므로, 다음으로는 숫자 2가 와야한다. 그러므로 idxMap.get(2)로 숫자 2가 저장된 인덱스(4)를 읽어온다. (minIndex)

인덱스들 간의 차이(거리)를 구하여 정답 배열에 저장하고, 수열의 두 번째 위치에는 2가 왔으므로 idxMap의 value들을 스왑해준다. numArr도 마찬가지로 스왑한다.

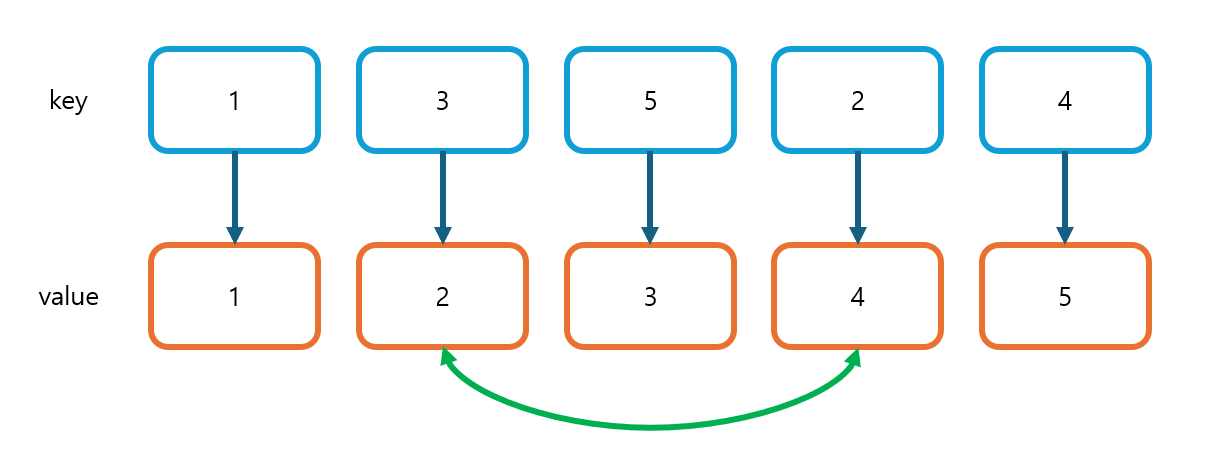
여기서 i번째, 즉 2번째 인덱스까지는 정렬이 완료되었으므로 answer[1]과 answer[2]의 값은 바뀔 일이 없다. 때문에 나중에 따로 루프를 N번만큼 더 돌리지 않고 미리 정답 출력 문자열을 갱신한다.

세 번째 루프도 위와 같은 작업을 수행하고, N번째까지 반복한다.

버전 (3)

다행히도 버전 2 코드는 채점을 통과했다. 그러나 다른 사람들의 코드를 보니 내 코드보다 2배는 빨랐다. 곰곰히 생각해보니 굳이 Map 자료구조를 쓰지 않아도 된다. 사용되는 모든 key와 value들은 1부터 N까지의 모든 정수이다. 즉, 배열의 인덱스와 매칭된다는 것이다.

또한 정렬된 부분은 더 이상 사용되지 않기 때문에 스왑이 아니라 일방적으로 인덱스 위치를 대입시키기만 해도 잘 동작한다. 아쉽게도 큰 성능 차이는 없었지만...

Map 자료구조를 배열로 대체하고, 약간의 개선을 수행한 코드는 다음과 같다. (최종버전, 수행 시간 664ms)

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;


public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;
        StringBuilder sb = new StringBuilder();

        int N = Integer.parseInt(br.readLine());

        // 각 숫자가 몇 번째 인덱스에 있는지 저장하고 있는 배열
        // Ex) [1, 3, 5, 2, 4]를 입력으로 받았을 때
        // idxArr[1]에는 1, [2]에는 4, [3]에는 2, [4]에는 5, [5]에는 3이 저장됨
        int[] idxArr = new int[N + 1];

        // 수열 A를 저장하고 있는 배열
        int[] numArr = new int[N + 1];

        // 각 숫자의 이동거리를 저장하는 배열
        int[] answer = new int[N + 1];

        st = new StringTokenizer(br.readLine());
        for (int i = 1; i <= N; i++) {
            int num = Integer.parseInt(st.nextToken());
            idxArr[num] = i;
            numArr[i] = num;
        }

        // 수열 A는 1부터 N까지 있으므로 1부터 시작
        for (int i = 1; i < N + 1; i++) {
            // 현재 최소값이 와야하는 위치의 값이 최소값이 아닌 경우
            if (numArr[i] != i) {
                // 정렬되지 않은 부분의 최소값이 저장된 위치
                int minIndex = idxArr[i];

                // 최소값이 저장된 위치와 현재 정렬하려는 위치 간의 거리
                int distance = minIndex - i;

                // 이동한 값들의 숫자에 거리 추가
                answer[numArr[i]] += distance;
                answer[numArr[minIndex]] += distance;

                // 선택 정렬에서 정렬된 부분까지는(배열의 인덱스 i까지) 더 이상 사용하지 않기 때문에
                // 값을 스왑하지 않고 인덱스 값을 대입해주기만 함
                idxArr[numArr[i]] = idxArr[i];
                numArr[minIndex] = numArr[i];
            }

            sb.append(answer[i]).append(' ');
        }

        System.out.println(sb);
    }
}

그리고 코드를 보면 알겠지만 모든 배열의 0번 방은 사용되지 않고 있다. 사실 배열의 크기를 N+1이 아니라 N으로 설정하여 모든 배열 공간을 사용할 수도 있었지만 그리 하지 않았다. 직관성도 떨어지고 정렬 구현 부분에 -1이나 +1 같은 자투리가 더 생겨서 가독성도 좋지 않아졌기 때문이다.

정리

이 문제 풀이의 핵심은 다음과 같다.

  1. 수열 A에는 1부터 N까지의 정수가 중복되지 않고 한 번씩 등장한다.
  2. 따라서 선택 정렬의 과정에서 다음으로 와야할 최소값을 알 수 있다.

입력

위의 내용을 응용하여 문제를 풀기 위해서 두 개의 배열을 생성한다. 참고로 직관적으로 배열의 인덱스와 입력값을 매칭시키기 위해 배열 크기를 N + 1로 설정했다. (모든 배열의 0번방은 쓰지 않는다.)

  • numArr[n + 1] : 수열 A를 저장하고 있는 배열
  • idxArr[n + 1]
    • AiA_i가 저장된 위치를 저장하고 있는 배열
    • 이 배열은 양의 정수 AiA_i번째 방에, AiA_i가 numArr에 저장된 위치를 저장한다.
    • 만약 이 배열을 맵이나 딕셔너리로 대체하려면 key에는 AiA_i를, value에는 AiA_i가 numArr에 저장된 위치를 저장한다.

따라서 데이터 입력 시 두 배열의 초기화는 이렇게 이루어진다.

// 각 숫자가 몇 번째 인덱스에 있는지 저장하고 있는 배열
// Ex) [1, 3, 5, 2, 4]를 입력으로 받았을 때
// idxArr[1]에는 1, [2]에는 4, [3]에는 2, [4]에는 5, [5]에는 3이 저장됨
int[] idxArr = new int[N + 1];

// 수열 A를 저장하고 있는 배열
int[] numArr = new int[N + 1];

// 각 숫자의 이동거리를 저장하는 배열
int[] answer = new int[N + 1];

st = new StringTokenizer(br.readLine());
for (int i = 1; i <= N; i++) {
    int num = Integer.parseInt(st.nextToken());
    idxArr[num] = i;
    numArr[i] = num;
}

정렬 및 루프

선택 정렬은 루프를 돌면서 배열의 현재 인덱스에 정렬되지 않은 값들 중 최소값이 와야한다. 그리고 이 문제에서는 현재 인덱스와 최소값이 위치한 인덱스의 차이를 구해야 하는거고.

만약 선택정렬을 직접 구현하게 되면 for문 두 개를 중첩해서 사용해야 한다. 따라서 시간복잡도는 O(n2)O(n^2)가 된다. 해당 문제는 입력 데이터의 길이인 N이 굉장히 크기 때문에 O(n2)O(n^2) 정도의 시간이면 시간 초과가 발생하는 것 같다.

여기서 우리는 배열을 순회하면서 현재 인덱스에 어떤 값이 와야하는지 알 수 있고, 그 값의 위치도 알고 있다. 왜냐? AiA_i는 1부터 N까지의 모든 양의 정수가 중복되지 않고 꼭 한 번씩 등장하기 때문이다. 이들의 위치를 저장하고 있는 배열(맵 또는 딕셔너리)도 만들었고.

그래서 위 내용을 구현하자면 다음과 같다.

// 수열 A는 1부터 N까지 있으므로 1부터 시작
for (int i = 1; i <= N; i++) {
    // 현재 최소값이 와야하는 위치의 값이 최소값이 아닌 경우
    if (numArr[i] != i) {
        // 정렬되지 않은 부분의 최소값이 저장된 위치
        int minIndex = idxArr[i];

        // 최소값이 저장된 위치와 현재 정렬하려는 위치 간의 거리
        int distance = minIndex - i;

        // 이동한 값들의 숫자에 거리 추가
        answer[numArr[i]] += distance;
        answer[numArr[minIndex]] += distance;

        // 선택 정렬에서 정렬된 부분까지는(배열의 인덱스 i까지) 
        // 더 이상 사용하지 않기 때문에
        // 값을 스왑하지 않고 인덱스 값을 대입해주기만 함
        idxArr[numArr[i]] = idxArr[i];
        numArr[minIndex] = numArr[i];
    }

    sb.append(answer[i]).append(' ');
}

System.out.println(sb);
profile
NCOOKIE
일단 해보자
이전 포스트

[SWEA][1859] 백만 장자 프로젝트

다음 포스트

[백준] 23883번 알고리즘 수업 - 선택 정렬 3

0개의 댓글

관련 채용 정보