https://www.acmicpc.net/problem/1719
코드 (1)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
static private StringBuilder sb = new StringBuilder();
static private ArrayList<Node>[] graph;
static private class Node {
int idx;
int weight;
public Node(int idx, int weight) {
this.idx = idx;
this.weight = weight;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int V = Integer.parseInt(st.nextToken());
int E = Integer.parseInt(st.nextToken());
graph = new ArrayList[V + 1];
for (int i = 1; i < V + 1; i++) {
graph[i] = new ArrayList<>(); // 그래프 초기화
}
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
// 이 그래프는 양방향임
graph[u].add(new Node(v, w));
graph[v].add(new Node(u, w));
}
for (int i = 1; i < V + 1; i++) {
dijkstra(i, V);
}
System.out.println(sb);
}
private static void dijkstra(int start, int V) {
int[] dist = new int[V + 1];
int[] parents = new int[V + 1];
Arrays.fill(dist, Integer.MAX_VALUE);
PriorityQueue<Node> queue = new PriorityQueue<>(Comparator.comparingInt(o -> o.weight));
queue.offer(new Node(start, 0));
dist[start] = 0;
while (!queue.isEmpty()) {
Node curNode = queue.poll();
if (dist[curNode.idx] > curNode.weight) {
continue;
}
for (int i = 0; i < graph[curNode.idx].size(); i++) {
Node nextNode = graph[curNode.idx].get(i);
int nextWeight = curNode.weight + nextNode.weight;
if (dist[nextNode.idx] > nextWeight) {
dist[nextNode.idx] = nextWeight;
// 최소 경로를 구한 노드의 부모 노드 기록
parents[nextNode.idx] = curNode.idx;
queue.offer(new Node(nextNode.idx, dist[nextNode.idx]));
}
}
}
traceRoute(parents, start);
}
// 부모 배열 사용하여 경로 역추적
private static void traceRoute(int[] parents, int start) {
for (int i = 1; i < parents.length; i++) {
if (i == start) {
sb.append("- ");
continue;
}
int answer = 0;
// 부모 노드가 start일 때까지 answer 갱신
for (int j = i; j != start; j = parents[j]) {
answer = j;
}
sb.append(answer).append(" ");
}
sb.append("\n");
}
}풀이 (1)
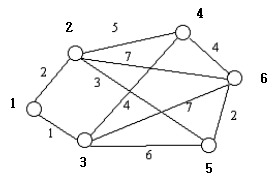
다익스트라 알고리즘을 수행하면 특정 노드의 부모 노드를 알 수 있다. 위 이미지에서 1을 출발점으로 삼는다고 할 때 4까지의 최단 경로는 1-2-4이다. 이 때 4의 부모는 2, 2의 부모는 1이다.
이러한 각 노드들의 부모를 알고리즘을 수행하며 기록하고, 모든 최단경로 탐색이 끝나면 해당 부모 노드를 역추적해서 출발점의 자식 노드를 찾으면 된다.
1에서 4까지 간다고 할 때 4의 부모 노드는 2, 2의 부모 노드는 1이다. 찾으려는 것은 출발점을 제외한 가장 처음으로 방문한 노드이므로 이 때 답은 2이다.
코드 (2)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
static private final StringBuilder sb = new StringBuilder();
static private ArrayList<Node>[] graph;
static int[][] result;
static private class Node {
int idx;
int weight;
public Node(int idx, int weight) {
this.idx = idx;
this.weight = weight;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int V = Integer.parseInt(st.nextToken());
int E = Integer.parseInt(st.nextToken());
result = new int[V + 1][V + 1];
graph = new ArrayList[V + 1];
for (int i = 1; i < V + 1; i++) {
graph[i] = new ArrayList<>(); // 그래프 초기화
}
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
// 이 그래프는 양방향임
graph[u].add(new Node(v, w));
graph[v].add(new Node(u, w));
}
for (int i = 1; i < V + 1; i++) {
dijkstra(i, V);
}
for (int i = 1; i < V + 1; i++) {
for (int j = 1; j < V + 1; j++) {
if (i == j) {
sb.append("-").append(" ");
} else {
sb.append(result[i][j]).append(" ");
}
}
sb.append("\n");
}
System.out.println(sb);
}
private static void dijkstra(int start, int V) {
int[] dist = new int[V + 1];
Arrays.fill(dist, Integer.MAX_VALUE);
PriorityQueue<Node> queue = new PriorityQueue<>(Comparator.comparingInt(o -> o.weight));
queue.offer(new Node(start, 0));
dist[start] = 0;
while (!queue.isEmpty()) {
Node curNode = queue.poll();
if (dist[curNode.idx] < curNode.weight) {
continue;
}
for (int i = 0; i < graph[curNode.idx].size(); i++) {
Node nextNode = graph[curNode.idx].get(i);
int nextWeight = curNode.weight + nextNode.weight;
if (dist[nextNode.idx] > nextWeight) {
dist[nextNode.idx] = nextWeight;
result[nextNode.idx][start] = curNode.idx;
queue.offer(new Node(nextNode.idx, dist[nextNode.idx]));
}
}
}
}
}풀이 (2)
이 문제의 그래프는 양방향 그래프이다. 이는 A에서 B까지의 최단경로와 B에서 A까지의 최단경로는 동일하다는 의미이다.
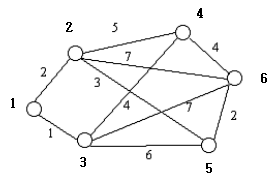
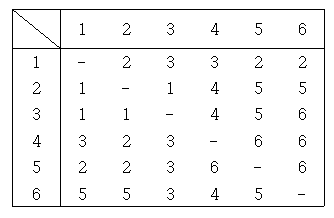
1에서 6까지의 최단 경로는 1-2-5-6이다. 6에서 1까지의 최단 경로는 이를 역순으로 한 6-5-2-1이다. 경로표의 1행 6열에는 2가, 6행 1열에는 5가 올 것이다. 즉, A행 B열에는 B에서 A까지의 최단 경로 중 도착점 직전의 노드가 온다는 것이다!
출발점 직후의 노드를 구하는 것과 달리 도착점 직전의 노드를 구하는 것은 굉장히 쉽다. 다익스트라 알고리즘 특성상 다음 노드에 접근하면서 최단 경로를 구하기 때문이다. 우리는 이 때 경로표를 갱신해주면 된다.
위의 구현에서는 경로표의 하나의 행(row)씩 구했지만, 여기서는 하나의 열(col)씩 구한다.
