두 정수 사이의 합
짝수의 합

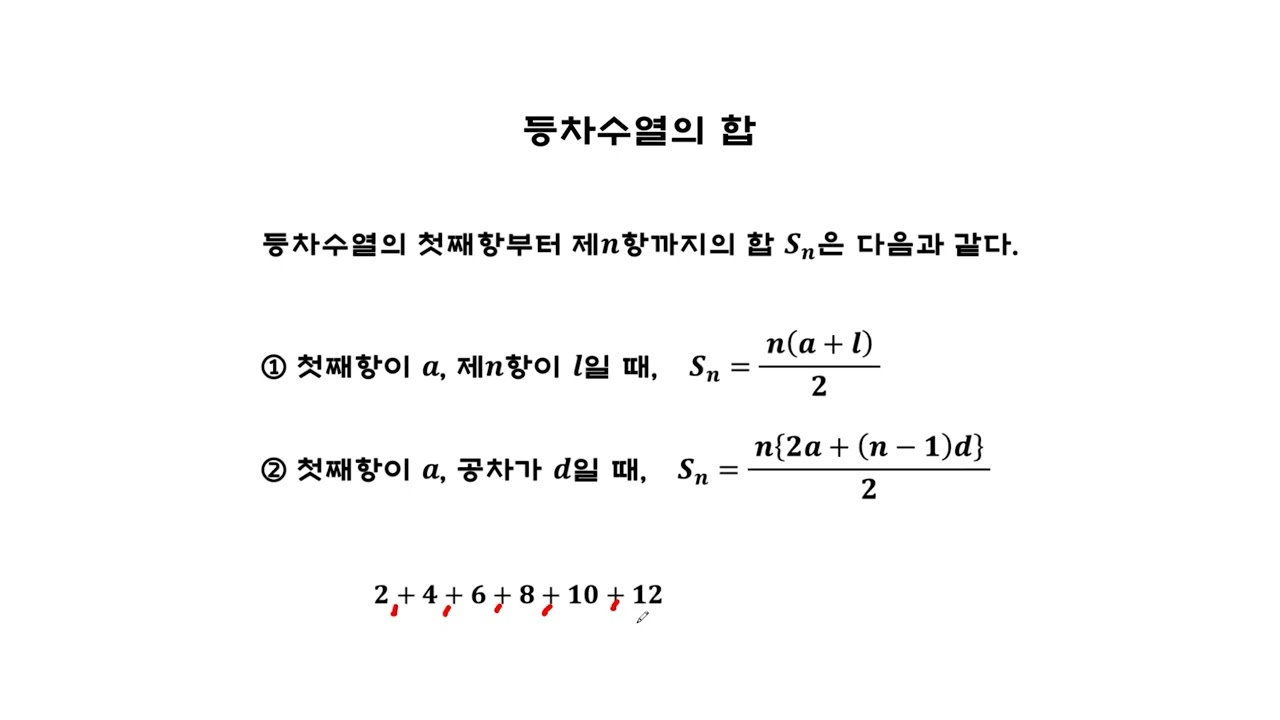
위의 두 문제 모두 등차수열의 합 공식을 사용해 간단하게 풀 수 있다.

두 정수 사이의 합

class Solution {
    public long solution(int a, int b) {
        if (a == b) {
            return a;
        }
        
        int min = a < b ? a : b;
        int max = a > b ? a : b;
        
        // 등차수열 합 공식 -> n(a + l) / 2
        return 1L * (max - min + 1) * (min + max) / 2;
    }
}

매개변수로 주어지는 두 정수 a, b 중 어떤 수가 더 큰지 모르기 때문에 삼항연산자 또는 Math.min(), Math.max() 메소드를 활용해 대소관계를 정한다. 이후 위 사진에서 첫 번째 식을 적용하면 루프를 돌리는 대신 간단하게 답을 구할 수 있다.

리턴 타입이 long이고 공식 계산 과정에서 값의 범위가 int의 표현 범위를 벗어날 수 있으므로 1L을 곱하게 해서 long 타입으로 변환시킨다.

참고로 이 코드처럼 min, max를 따로 구하지 않아도 1L * (Math.abs(a - b) + 1) * (a + b)처럼 절대값을 사용해서 계산할 수 있다.

짝수의 합

class Solution {
    public int solution(int n) {
        return (n / 2) * (n / 2 + 1);
    }
}

공차 d가 있을 때의 등차수열의 합 공식을 활용하면 된다. 이 때 첫째항 $a$는 2, 공차 $d$는 2, 수열의 개수 $n$은 n / 2인데, 계산의 용의성을 위해 n / 2 대신 $k$라고 하자.. 이들을 해당 식에 대입해서 여차저차 정리하면...

여기서 ( a = 2 ), ( d = 2 ) 를 대입하면:

따라서 짝수들의 합을 구하는 공식은 다음과 같다.

이 때 n / 2 대신 $k$로 대체했었으므로 다시 대입하면 위와 같은 코드가 된다.

후기

프로그래밍 좀 배웠다고 오히려 생각이 좁아진 것인지 간단한 수학 공식을 응용하면 되는걸 컴퓨터를 고생시키고 있었다. 조심하자.

참고

• [수열] 등차수열의 합 - 공식