비숍

코드

[ 시간초과 코드 ]

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int N,ans,in;
int arr[12][12];
vector<pair<int,int>> v;
bool isused1[30];
bool isused2[30];
void func(int start, int size){
    if(start == v.size()){
        ans = max(ans, size);
        return;
    }else{
        for(int i=start;i<v.size();i++)
        {
            int y = v[i].first;
            int x = v[i].second;
            if(isused1[x+y] || isused2[x-y+(N-1)]) continue;
            isused1[x+y] = true;
            isused2[x-y+(N-1)] = true;
            func(i+1, size+1);
            isused1[x+y] = false;
            isused2[x-y+(N-1)] = false;
        }
    }
}
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);

    cin >> N;
    for(int i=0;i<N;i++)
        for(int j=0;j<N;j++)
        {
            cin >> in;
            if(in) v.push_back({i,j});
        }
    func(0,0);
    cout << ans;
    return 0;
}

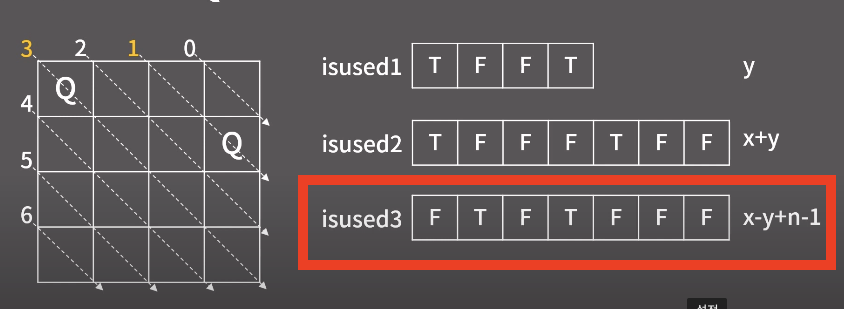
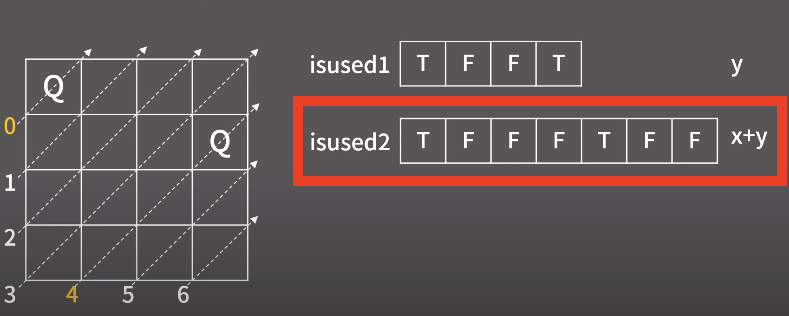
• 핵심
  : N-Queen문제를 풀때 사용했던 대각선 2개에 대해 isused[]를 선언해 해결
  

• 문제
  : 시간초과 발생

---

[ 정답 코드 ]

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int N,ans,in,bc,wc;
vector<pair<int,int>> b;
vector<pair<int,int>> w;
bool isused1[30];
bool isused2[30];
void black(int start, int size){
    if(start == b.size()){
        bc = max(bc, size);
        return;
    }else{
        for(int i=start;i<b.size();i++)
        {
            int y = b[i].first;
            int x = b[i].second;
            if(isused1[x+y] || isused2[x-y+(N-1)]) continue;
            isused1[x+y] = true;
            isused2[x-y+(N-1)] = true;
            black(i+1, size+1);
            isused1[x+y] = false;
            isused2[x-y+(N-1)] = false;
        }
    }
}
void white(int start, int size){
    if(start == w.size()){
        wc = max(wc, size);
        return;
    }else{
        for(int i=start;i<w.size();i++)
        {
            int y = w[i].first;
            int x = w[i].second;
            if(isused1[x+y] || isused2[x-y+(N-1)]) continue;
            isused1[x+y] = true;
            isused2[x-y+(N-1)] = true;
            white(i+1, size+1);
            isused1[x+y] = false;
            isused2[x-y+(N-1)] = false;
        }
    }
}
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);

    cin >> N;
    for(int i=0;i<N;i++)
        for(int j=0;j<N;j++)
        {
            cin >> in;
            if(in){
                /* 좌표가 black인지 판별 */
                if((i%2==0 and j%2==0)||(i%2==1 and j%2==1)){
                    b.push_back({i,j});
                }else{
                    w.push_back({i,j});
                }
            } 
        }
    black(0,0);
    white(0,0);
    cout << wc+bc;
    return 0;
}

• 문제 해결
  : 기존 코드 로직 + 흰색과 검은색 체스판은 서로 영향을 주지 않아서 서로 나눠서 해결해야 한다는 아이디어가 필요
  
• 이러한 체스판에서 비숍이 대각선으로 움직일 때 흰색과 검은색 자리는 서로 영향을 주지 않는다!
  --> 입력을 분할하고 2개의 재귀로 분할
  --> 시간 감소