[CS 정리] 알고리즘 (Algorithm)

김정욱·2021년 5월 26일

algorithm computer science 면접준비

면접준비

목록 보기

2/6

다양한 정렬

Ref : https://github.com/neity16/tech-interview-for-developer

버블 정렬(Bubble Sort)

동작

인접한 인자와 비교하여 더 큰 원소를 뒤로 보내는 정렬 방식

시간복잡도 = O(N^2)

공간복잡도 = O(N) --> 추가로 공간을 필요로하지는 않고 기존 배열만큼만 사용

선택 정렬(Selection Sort)

동작

현재 자리에 현재 차례에 해당하는 가장 작은 값을 가져와서 정렬

시간복잡도 = O(N^2)

공간복잡도 = O(N)

삽입 정렬(Insertion Sort)

동작

2번째 원소부터 시작해서 그 앞 원소들과 비교해서 삽입할 위치를 정한 후 선택된 위치에 원소를 삽입하는 정렬

선택정렬과 유사하지만 최선의 경우 O(N)이라는 효율성을 가짐

시간복잡도 O(N^2) / 최선의 경우 O(N)

공간복잡도 O(N)

퀵 정렬(Quick Sort)

동작
1) 피벗을 선택한 후
2) 오른쪽에서는 왼쪽으로 이동하면서 피벗보다 작은 수를 찾는다
3) 왼쪽에서는 오른쪽으로 이동하면서 피벗보다 큰 수를 찾는다
4) 2,3번에서 찾은 두 수를 교환한다.
5) 2~4를 더 이상 진행할 수 없을 때 까지 반복하고 엇갈린 자리중 작은값을 피벗과 자리 교환
6) 결과적으로 피벗을 중심으로 왼쪽은 피벗보다 작은수, 오른쪽은 큰 수가 정렬됨
7) 정렬된 두 집단에서 다시 피봇을 정해서 반복!

평균적으로 O(NlogN)의 시간복잡도

O(N)의 공간복잡도

분할 정복 기법으로 동작(최악의 경우 제외하고)

가장 작거나 큰 값을 피벗으로 설정할 경우 분할되지 않아서 O(N^2)를 가짐

서로 먼 거리에 있는 요소를 교환하면서 속도를 줄일 수 있음

불안정 정렬
: 같은 값을 가지는 요소의 순서가 보장되지 않음

합병 정렬(Merge Sort)

동작

영역을 쪼갤 수 있을 때 까지 쪼갠 뒤 합병(merge)하면서 정렬 수행

순차적인 비교로 정렬을 진행하므로 Linked-list 정렬이 필요할 때 매우 효율적
--> 삽입 삭제 연산이 O(1)이라서 효율적
(접근 연산은 O(N)이 소요되므로 퀵 정렬을 하면 비효율적이다)

퀵 정렬과는 다르게 안정 정렬에 속함
: 같은 값을 정렬할 때 순서가 보장됨

평균, 최선, 최악 모두 O(NlogN)

공간복잡도는 O(N)

힙 정렬(Heap Sort)

동작
1) Heapify 연산을 통해 최대 or 최소 heap구조로 변환
2) root값을 가장 마지막 원소와 교환
3) 힙의 사이즈를 하나 감소
4) 1~3 반복

완전 이진트리를 기본으로하는 힙(Heap) 자료구조를 기반으로 한 정렬

시간복잡도 : O(NlogN)

퀵정렬과 합병정렬의 성능이 좋아 자주 사용되지는 않는다

가장 큰 값을 구할 때 효율적 --> heapify는 O(logN)밖에 안걸리기 때문

기수 정렬(Radix Sort)

동작

모든 원소의 기본 요소(Radix)를 이용하여 정렬을 진행
1) 모든 원소의 1의 자리 수를 비교해서 정렬
2) 1의 결과를 바탕으로 10의 자리 수를 비교해서 정렬
3) n자리수까지 비교를 반복
4) 마지막 자리수까지 검사하면 정렬 완료

특정 자리수를 이용해 정렬을 진행

비교를 하지 않기 때문에 빠른 시간복잡도를 가짐

시간복잡도는 O(d*N) / d=정렬할 숫자의 자리수를 의미

제한 사항

길이가 같은 원소만 비교 가능

버킷이라는 추가적인 메모리 공간이 필요

계수 정렬(Counting Sort)

동작

각 숫자가 몇 번 등장했는지 센 뒤 작은 값부터 출력하면 정렬이 된다.

안정 정렬
: 같은 값의 순서가 보장된다

시간복잡도 : O(N)

기수정렬과 마찬가지로 비교를 하지 않기 때문에 빠른 정렬 이 가능

제한

정렬하는 숫자가 특정한 범위 내에 있을 때만 사용 가능

해당 숫자 범위 만큼 메모리가 필요 --> 낭비가 심함

안정 vs 불안정

안정 정렬

버블 정렬

삽입 정렬

병합 정렬

계수 정렬

기수 정렬

불안정 정렬

퀵정렬

선택 정렬

힙 정렬

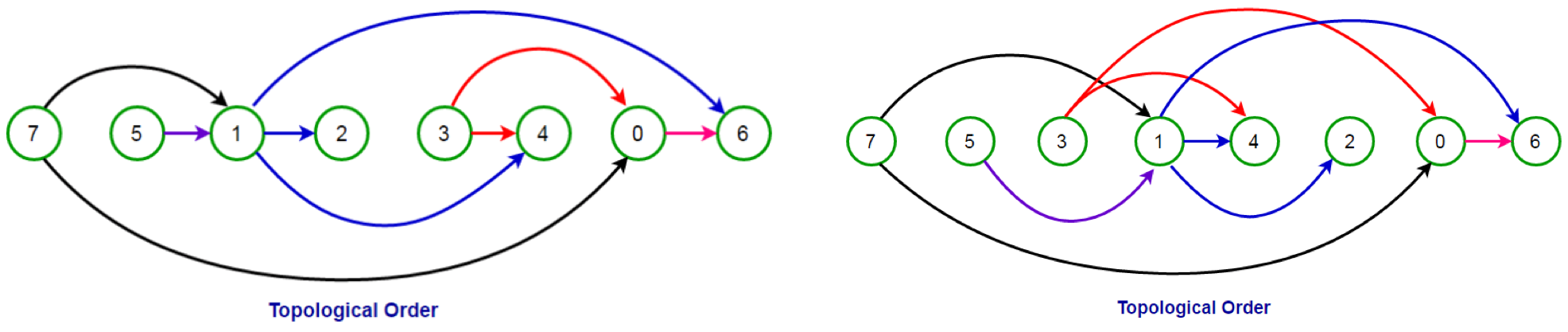
위상 정렬(Topological Sort)

개념

순서가 정해져있는 작업을 차례로 수행해야 할 때, 그 순서를 결정해주는 알고리즘

여러개의 경로가 존재할 수 있음 --> 여러개의 답이 존재할 수 있다!

반드시 그래프는 DAG(Directed Acyclic Graph) 여야 한다

시간복잡도 = O(V+E)

조건 & 구현

DAG(Directed Acyclic Graph)

사이클이 존재하지 않는 방향 그래프

스택 / 큐 를 이용해서 구현 가능 --> 보통은 큐를 많이 사용

진입 차수(indegree)

해당 노드를 향한 방향의 수 (받는 화살표의 수)

로직

모든 노드의 진입 차수 계산

진입 차수가 0인 노드를 큐에 삽입

큐에서 꺼낸 노드에 연결된 간선을 제거

제거 후 진입 차수가 0이 된 노드를 큐에 삽입

큐가 빌 때 까지 앞 과정을 반복

알고리즘 분류

그리디(욕심쟁이) 알고리즘

동적프로그래밍(DP)이 지나치게 많은 일을 하는 것에서 착안된 알고리즘
--> DP를 보완하는 알고리즘 이다.

당장 눈 앞에 보이는 최적의 상황만을 쫓는 알고리즘

부분에서의 최적의 해가 전체적인 최적의 해가 되는 경우!

무조건 큰 경우대로 / 작은 경우대로 처럼 극단적으로 문제에 접근한다
--> 정렬(sort)기법과 함께 사용되는 경우가 많다

ex) 거스름돈 주기 : 무조건 큰 화폐부터 거슬러 주면 된다 ! (최적의 해)

백트래킹 알고리즘

특정 조건을 만족하는 모든 경우의 수에 대해 수행하는 알고리즘

해를 찾는 도중 해가 아니어서 막히면, 되돌아가서 다시 해를 찾아가는 기법

브루트포스(완전탐색)과 유사하지만, 특정 조건을 만족하는 경우의 수를 수행한다는 차이점이 있음

해를 찾아가는 도중, 지금의 경로가 해가 될 것 같지 않으면 그 경로를 더이상 가지 않고 되돌아 간다
--> 이것을 가지치기 한다고 한다

주된 사용
: DFS등으로 모든 경우의 수를 탐색하는 과정에서,
조건문 등을 걸어서 답이 절대로 될 수 없는 상황을 정의하여
그러한 상황에서 탐색을 중지시킨 뒤 돌아가서 다른 경우를 탐색하게 한다.

예시 문제
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int N, M;
int arr[10];
bool isused[10];
void func(int depth){
    if(depth == M){
        for(int i=0;i < M;i++)
            cout << arr[i] << ' ';
        cout << '\n';
        return;
    }else{
        /* 백트래킹 핵심 부분 */
        for(int i=1;i<=N;i++)
        {
            if(!isused[i]){
                arr[depth] = i;
                isused[i] = true;
                func(depth+1);
                isused[i] = false;
            }
        }
    }
}
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);

    cin >> N >> M;
    func(0);
    return 0;
}

최단 경로 알고리즘

다익스트라 최단경로 알고리즘

[ Intro ]

그래프에서 정점끼리 최단 경로를 구하는 방법

하나의 정점 --> 다른 하나의 정점까지 최단경로

하나의 정점 --> 다른 모든 정점까지의 최단경로

Dijkstra 알고리즘

벨만-포드 알고리즘

하나의 목적지로가는 모든 최단 경로

모든 정점끼리의 최단 경로를 구하는 문제

플로이드 워셜 알고리즘

다익스트라 최단경로 알고리즘은 하나의 정점 --> 다른 모든 정점까지 최단경로 에 해당

[ 로직 ]

모든 노드간 이동거리 배열을 INF(큰 값)으로 초기화

출발 노드(정해짐)를 통해 갈 수 있는 경로 갱신

갱신된 테이블을 통해 방문하지 않은 노드 중 최단거리가 가장 짧은 노드를 선택

노드 간 이동거리가 더짧다면 갱신하며 수행

다시 방문하지 않은 노드 중 최단거리가 가장 짧은 노드를 선택 후 반복!

[ 설명 ]

다익스트라가 제시안 최단경로 알고리즘

현재 노드에 연결된 정점까지 최소 경로를 갱신한 뒤, 현재를 기준으로 방문하지 않은 점 들 중거리가 가장 짧은 노드를 선택하는 알고리즘
--> 한 단계당 하나의 노드에 대한 최단 거리를 확실히 찾는다

현재 상황에서 최선을 선택한다는 원리로 '그리디 알고리즘'으로 분류된다

간선이 음의 값을 가지면 성립되지 X
--> 이 경우 벨만-포드 알고리즘을 사용해야 한다

단순 값이 아닌 경로를 찾기 위해서는 추가적인 코드가 필요

구현 방법에 따라 시간복잡도가 상이하다

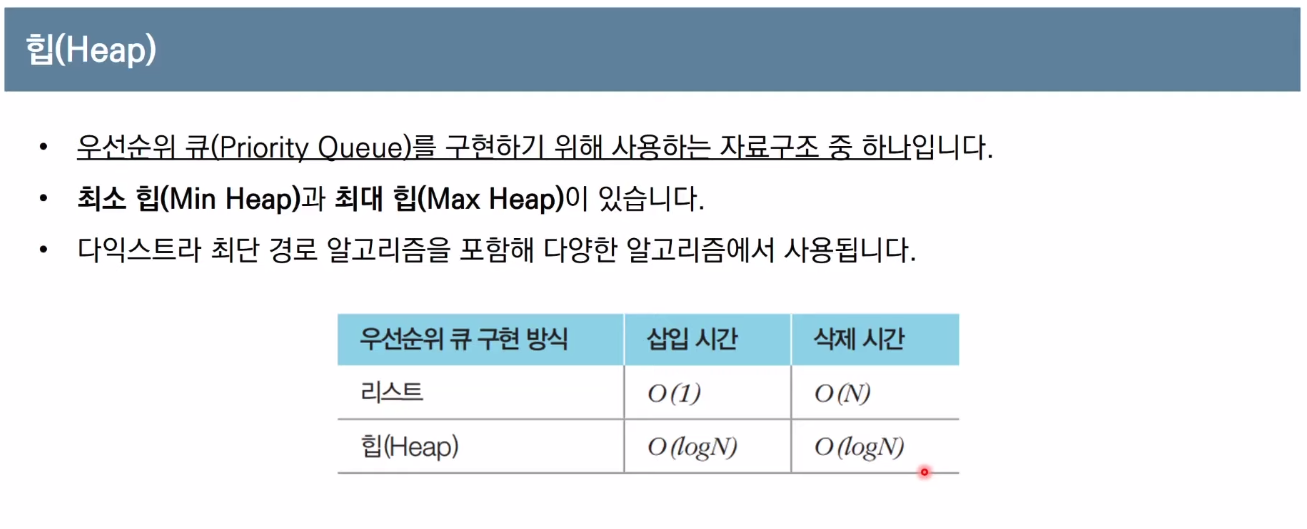
배열로 구현 -> O(V^2)

우선순위 큐로 구현 -> O(ElogE) --> O(ElogV)
(모든 간선은 한번씩 수행 O(E) + 우선순위 큐를 통해 값을 추출 O(logE) = O(ElogE))
: Heap 자료구조를 사용하면 노드를 선택하는 과정을 O(N)이 아닌 O(logN)으로 가능
(최대 힙 -> 값이 큰 값이 먼저 나옴
최소 힙 -> 값이 작은 값이 먼저 나옴)

[ 예시 & 코드 ]

priority_queue를 이용한 Dijkstra
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
#define INF 1e9 // 10억을 의미
using namespace std;
vector<pair<int,int>> graph[30001]; // 0인덱스는 사용하지 X
int dis[30001]; // 0인덱스는 사용하지 X
void dijkstra(int start){
    priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> pq;
    pq.push({0, start});
    dis[start] = 0;
    while(!pq.empty())
    {
        int dist = pq.top().first; // 비용
        int now = pq.top().second; // 현재 거쳐가는 지점의 인덱스
        pq.pop();
        if(dis[now] < dist) continue;
        /* i는 의미 없고 그냥 순회하기 위한 변수 */
        for(int i=0;i<graph[now].size();i++)
        {
            /* first-> 목적지 , second -> 목적지 까지 필요한 비용 */
            int cost = dist + graph[now][i].second; // 비용 계산
            if(cost < dis[graph[now][i].first]){ // first에는 목적지가 들어가있고 현재 기록된 값이랑 비교 검사
                dis[graph[now][i].first] = cost;
                // first까지 가는데 들어가는 비용 cost를 갱신하고 pq에 삽입
                pq.push({cost, graph[now][i].first});
            }
        }
    }
}
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    int N, M, C;
    int cnt=0, MAX=0;
    cin >> N >> M >> C;
    fill(dis, dis+30001, INF);
    for(int i=0;i<M;i++)
    {
        int a,b,c;
        cin >> a >> b >> c;
        graph[a].push_back({b,c});
    }
    dijkstra(C);
    for(int i=1;i<=N;i++)
        if(dis[i] != INF){
            cnt++;
            MAX = max(MAX, dis[i]);
        }
    cout << cnt-1 << ' '<< MAX << '\n';
    return 0;
}

벨만 포드 알고리즘

ref : https://ssungkang.tistory.com/entry/Algorithm-%EB%B2%A8%EB%A7%8C%ED%8F%AC%EB%93%9CBellman-Ford-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
https://victorydntmd.tistory.com/104
https://yabmoons.tistory.com/365

[ 설명 ]

한 노드 -> 다른 모든 노드 까지의 최단경로를 계산하는 알고리즘

음수의 가중치를 가진 경우에도 최단 경로를 구할 수 있음
(다익스트라의 한계 극복 / 시간복잡도는 더 높다)

시간복잡도 = O(|V||E|) = O(V^3)
(그래프의 간선이 많으면 보통 정점 개수의 제곱 정도로 존재 / O(E) = O(V^2))

음의 가중치를 갖는 상황에서 순환(Cycle)이 생기면 경로가 계속 짧아지지만, 이것은 실질적인 최단 경로가 아니다
--> 벨만 포드의 핵심은 순환을 포함하지 않으며, 경로의 길이가 최대 |V|-1을 가진다는 것!

Relax 연산

해당 정점에서 더 낮은 가중치로 도달할 수 있는 경우, 그 값을 갱신해 주는 과정
(모든 정점 중 한 번이라도 계산된 정점에 연결된 간선을 통해 갱신 수행!)

음의 Cycle 검사

Relax연산을 V(N-1)까지 수행하면 최단 거리가 나오도록 설계가 되어있다

만약 V(N)에 대해 Relax연산을 수행했는데 최단 경로가 갱신되면 음의 Cycle인 경우라고 판단 가능!

[ 로직 ]

출발 정점(V1)의 거리는 0 / 다른 정점까지 거리는 INF로 초기화

모든 정점(V1 ~ VN)중 한 번이라도 계산된 정점에 대해서만 연결된 간선을 통해 최소 경로인 경우 갱신

한 번이라도 계산된 정점(dist가 INF가 아닌 정점)만 선택해야 하는 이유!
--> 한번도 경유하지 않은 점은 거쳐서 갈 수 없기 때문에 간선의 비용이 짧아도 유효하지 X

출발 정점을 V2 ~ VN까지 확장해서 앞 과정을 반복!
--> 즉, V1 ~ V(N-1)까지 각 Relax 연산을 수행
--> 하지만, 보통 음의 Cycle을 검사하기 위해 V(N)까지 수행

[ 코드 ]
#include <iostream>
#include <vector>
using namespace std;

#define INF 987654321

int dist[502];
vector<pair<int,int>> v[502];

int main(){
    ios_base :: sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    // 정점,간선의 수
    int N,M;
    cin >> N >> M;

    bool cycle = false;

    for (int i=0;i<M;i++){
        int node1,node2,w;
        cin >> node1 >> node2 >> w;
        v[node1].push_back(make_pair(node2, w));
    }

    for (int i=1;i<=N;i++){
        dist[i] = INF;
    }

    dist[1] = 0;
  	// 경로의 길이는 N-1 이고 N 이 된다면 음수사이클 생긴다.
    for (int i=1;i<=N;i++){
        // 모든 정점에 대해서 모든 간선을 탐색한다.
        for (int j=1;j<=N;j++){
            for (auto &n : v[j]){
              	// 방문되지 않은 지점에서 출발은 SKIP
                if (dist[j] != INF && dist[n.first]>n.second + dist[j]){
                    dist[n.first] = n.second + dist[j];
                    if (i==N) cycle = true;
                }
            }
        }
    }

    if (cycle) cout << "-1\n";
    else {
        for (int i=2;i<=N;i++){
            if (dist[i] == INF) cout << "-1\n";
            else cout << dist[i] << "\n";
        }
    }
}

플로이드 워셜 알고리즘

[ 설명 ]

모든 노드 -> 다른 모든 노드까지의 최단경로 모두 계산하는 알고리즘
다익스트라 알고리즘과 마찬가지로 거쳐가는 노드를 기준으로 알고리즘을 수행
2차원 배열을 통해 모든 노드간 최단거리를 기록
2차원 테이블 배열을 점화식에 따라 갱신한다는 점에서 DP에 속함
: 점화식에 맞게 배열을 갱신한다
시간복잡도가 무조건 O(V^3)이기 때문에 플로이드 워셜을 쓰는 문제의 입력은 500을 넘지 않게 주어진다

[ 코드 ]

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
#define INF 1e9 // 10억을 의미
using namespace std;
int graph[501][501];
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    int N,M;
    cin >> N >> M;
    /* 최단거리 테이블을 모두 무한으로 초기화 */
    for(int i=0;i<501;i++)
        fill(graph[i], graph[i]+501, INF);
    /* 자기 자신으로 가는 비용은 0으로 초기화 */
    for(int a=1;a<=N;a++)
        for(int b=1;b<=N;b++)
            if(a==b) graph[a][b] = 0;
    for(int k=1;k<=N;k++)
    {
        for(int a=1;a<=N;a++)
        {
            for(int b=1;b<=N;b++)
                /* a-> 출발노드, b-> 도착노드 , k-> 경유 노드 */
                graph[a][b] = min(graph[a][b], graph[a][k]+graph[k][b]);
        }
    }
    /* 수행된 결과를 출력 */
    for(int a=1;a<=N;a++)
    {
        for(int b=1;b<=N;b++)
        {
            if(graph[a][b] == INF)
                cout << "INF" << ' ';
            else
                cout << graph[a][b] << ' ';
        }
        cout << '\n';
    }
    return 0;
}

3중 for문을 통해 각 모든 점에 대해 기존 경로 vs 경유 경로를 검사해서 작은 경로로 update!
구현 난이도는 Dijkstra보다 낮다

MST 알고리즘

크루스칼(Kruskal) 알고리즘

[ 필요 지식 ]

신장 트리(Spanning Tree)

그래프에서 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프(무향 그래프)
( 모든노드 포함 + 사이클 X )

최소 신장 트리 (MST = Minimum Spanning Tree)

최소한의 비용으로 구성되는 신장 트리

[ 설명 ]

최소 신장 트리를 구하는 알고리즘 중 하나
(MST를 구하는 다른 알고리즘으로 프림(Prim) 알고리즘이 있음 )

Union-Find 알고리즘 이 사용

Union : 두 집합을 합치는 연산

최초 모든 노드는 parent로 자기 자신을 가지고 있다

두개의 노드 중 더 큰 번호에 해당하는 노드의 부모노드를 작은 노드로 갱신!

Find : 연결된 루트 노드를 찾는 것(여기서는 부모 노드를 찾는 것)

재귀적으로 구현하여 연결된 가장 부모 노드를 찾는다
--> findParent 구현시 부모 테이블 값을 바로 갱신하면 '경로 압축'이 가능함!

크루스칼(Kruskal) 알고리즘 로직
1) 모든 간선에 대해 오름차순 정렬
2) 아직 처리하지 않은 간선 중 가장 짧은 간선을 선택
3) 사이클이 없으면(부모 노드가 같지 않으면) 현재 MST에 추가
(사이클이 있으면 제외)

[ 코드 ]
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;
int N,M,ans,max_cost;
int parent[100002]; // 1~100000 사용
/* find 연산 */
int findParent(int x){
    if(x == parent[x]) return x;
    return parent[x] = findParent(parent[x]);
}

/* union 연산 */
void unionParent(int a, int b){
    a = findParent(a);
    b = findParent(b);
    if(a<b) parent[b] = a;
    else parent[a] = b;
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    cin >> N >> M;
    vector<pair<int, pair<int,int>>> edges;
    for(int i=0;i<M;i++)
    {
        int a, b, cost;
        cin >> a >> b >> cost;
        edges.push_back({cost,{a,b}});
    }
    // parent 초기화
    for(int i=1;i<=N;i++)
        parent[i] = i;

    // edges 정렬
    sort(edges.begin(), edges.end());

    for(int i=0;i<edges.size();i++)
    {
        int a = edges[i].second.first;
        int b = edges[i].second.second;
        int cost = edges[i].first;
        if(findParent(a) != findParent(b)){
            unionParent(a,b);
            max_cost = max(max_cost, cost);
            ans += cost;
        }
    }
    cout << ans - max_cost;
    return 0;
}
findParent

find 연산

return parent[x] = findParent(parent[x]); 를 통해서 경로 압축을 바로 구현
--> 바로 위 부모가 아니라 루트를 가리킬 수 있도록 바로바로 갱신!

findUnion : union 연산

parent 초기화

edges 정렬

MST 추가

짧은 cost 순서대로 사이클이 형성하지 않으면 현재 MST에 추가

프림(Prim) 알고리즘

ref :
https://www.weeklyps.com/entry/%ED%94%84%EB%A6%BC-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-Prims-algorithm
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=kimmy5000&logNo=220635475967

개념

무향 연결 그래프가 주어질 때, MST를 구하는 알고리즘

크루스칼(Kruskal) 알고리즘과 목적이 같으나, 로직이 다름

프림은 정점(V) 위주 / 크루스칼은 간선(E) 위주

로직

임의의 정점을 선택하여 T에 추가 (T는 트리)

T에 있는 노드와 T에 없는 노드 사이의 간선 중 가중치가 최소인 간선을 찾는다
(트리에 있는 노드와, 없는 노드 사이 간선 중 최소를 구하기에 따로 Cycle 검사 로직이 필요 없음)

찾은 간선이 연결하는 노드 중 T에 없는 노드를 T에 추가

모든 노드가 T에 포함될 때 까지 앞 과정 반복

크루스칼(Kruskal) 알고리즘과 차이점

로직

프림(Prim) : 정점을 선택하고 그것과 연결된 가장 적은 비용의 간선을 선택하는 방식

크루스칼(Kruskal) : 모든 간선의 비용중 적은 비용의 간선을 선택하는 방식

구성 방식

프림(Prim) : 정점들이 계속 연결되는 방식

크루스칼(Kruskal) : 서로 다른 정점들의 집합이 합쳐지는 방식

시간복잡도(Time Complexity) / E=간선의 수 , V=정점의 수

프림(Prim)

unsorted array로 구현 : O(V^2)

priority queue로 구현 : O(ElogV)

크루스칼(Kruskal) : O(ElogV)

이진 탐색

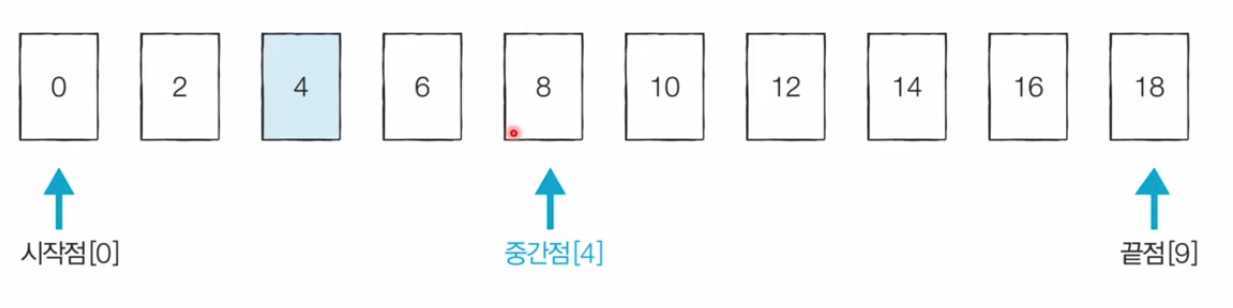
[ 설명 ]

정렬된 상태에서 원소를 O(logN)의 시간복잡도로 찾는 탐색

주로 파라메트릭 서치 유형 문제 풀이로 많이 사용됨

입력의 크기가 매우 큰 상황에서 일정 조건으로 탐색을 해야하면 이진탐색을 가장먼저 떠올려야 한다

특정 수의 개수를 구하는 과정을 O(logN)으로 수행할 수 있음

C++에서 upper_bound와 lower_bound를 이용해 countByRange를 정의한 후 leftValue와 ```rightValue에 같은 값을 넣으면 특정 수의 개수를 구할 수 있음

C++ STL에 binary_search()가 구현되어 있으나 지정 값을 찾는기능에 제한된다
/* stl container */
  binary_search(arr.begin(), arr.end(), M);
/* array */
  binary_search(arr, arr+N, M);
[ 코드 - 반복문을 통한 이진탐색 구현 ]
#include <cstdio>
#include <vector>
#include <queue>
#include <iostream>
#include <cmath>
#include <algorithm>
#define ll long long
using namespace std;
ll N,M,high;
vector<ll> arr(1000002);
/* 이진탐색 - O(logN) */
void bs(vector<ll>& arr, ll st, ll en){
    ll ans=0;
    while(st <= en)
    {
        ll tot=0;
        ll mid = (st + en)/2;
        for(auto a : arr)
            if(a > mid)
                tot += a-mid;
        if(tot < M)
            en = mid-1;
        else{
            ans = mid;
            st = mid + 1;
        }
    }
    cout << ans;
}
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    cin >> N >> M;
    for(int i=0;i<N;i++)
    {
        cin >> arr[i];
        high=max(high,arr[i]);
    }
    bs(arr,0,high);
    return 0;
}

이분매칭 알고리즘

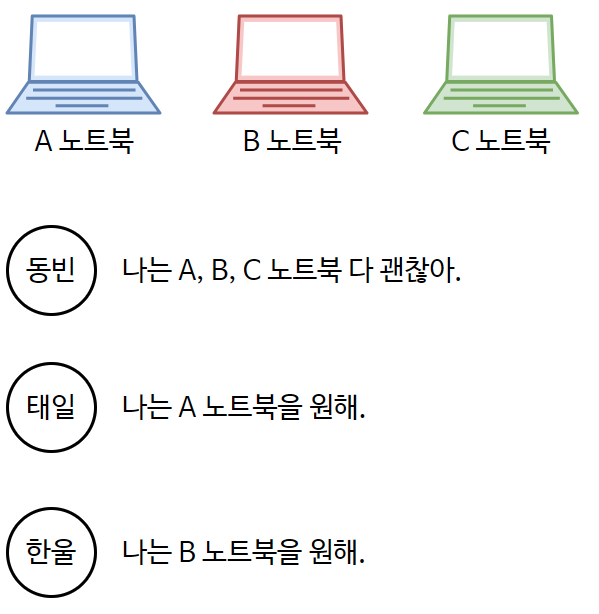
(Ref : https://blog.naver.com/PostView.nhn?blogId=ndb796&logNo=221240613074&redirect=Dlog&widgetTypeCall=true&directAccess=false)

[ 설명 ]

두 집단 사이에서 Max Matching되는 경우를 구하는 것

노트북 집단과 사람 집단에서 최대로 연결될 수 있는 경우를 구하는 것
핵심
: 내가 선택하려는 노드가 이미 선택되어 있을 때
그것을 선택한 노드에게 다른 노드를 선택할 수 있도록 권장하는 것

[ 예시 코드 ]

#include <cstdio>
#include <vector>
#include <queue>
#include <iostream>
#include <cmath>
#include <algorithm>
#include <set>
#define ll long long
using namespace std;
vector<pair<int,int>> v(1010);
int work[1010];
bool finish[1010];
int T, N, M;
/* 이분 탐색 */
bool DFS(int x){
    for(int t=v[x].first;t<=v[x].second;t++)
    {
        if(finish[t]) continue;
        finish[t] = true;
        if(work[t] == -1 || DFS(work[t])){
            work[t] = x;
            return true;
        }
    }
    return false;
}
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    cin >> T;
    while(T--)
    {
        v.clear();
        cin >> N >> M;
        for(int i=0;i<M;i++)
        {
            int a, b;
            cin >> a >> b;
            v.push_back({a,b});
        }
        /* 연결된 점의 좌표 초기화 */
        fill(work, work+1010, -1);
        int ans=0;
        /* 모든 점들에 대해 연결 */
        for(int i=0;i<M;i++)
        {
            /* 정점 방문 여부 초기화 */
            fill(finish, finish+1010, false);
            if(DFS(i)) ans++;
        }
        cout << ans << '\n';
    }
    return 0;
}

BOJ 9576

DFS / BFS

[ DFS ]

그래프의 탐색 방법의 한 종류

깊이를 우선으로 갈 수 있는 만큼 최대한 탐색한 뒤 더 이상 갈 수 없다면 이전 정점으로 돌아가는 방식

구현

stack 사용

재귀(recursive)

시간복잡도 (V=정점의 수 / E=간선의 수)

그래프를 인접 행렬로 표현 --> O(V^2)

그래프를 인접 리스트로 표현 --> O(V+E)

[ BFS ]

그래프의 탐색 방법의 한 종류

넓이를 우선으로 순차적으로 인접한 노드부터 탐색하는 방법

구현

큐(queue)를 통한 구현

시간복잡도 (V=정점의 수 / E=간선의 수)

그래프를 인접 행렬로 표현 --> O(V^2)

그래프를 인접 리스트로 표현 --> O(V+E)

김정욱

Developer & PhotoGrapher

이전 포스트

[CS 정리] 자료 구조(Data Structure)

다음 포스트

[CS 정리] 알고리즘 (Algorithm)

면접준비

다양한 정렬

버블 정렬(Bubble Sort)

선택 정렬(Selection Sort)

삽입 정렬(Insertion Sort)

퀵 정렬(Quick Sort)

합병 정렬(Merge Sort)

힙 정렬(Heap Sort)

기수 정렬(Radix Sort)

계수 정렬(Counting Sort)

안정 vs 불안정

위상 정렬(Topological Sort)

개념

조건 & 구현

로직

알고리즘 분류

그리디(욕심쟁이) 알고리즘

백트래킹 알고리즘

예시 문제

최단 경로 알고리즘

다익스트라 최단경로 알고리즘

[ Intro ]

[ 로직 ]

[ 설명 ]

[ 예시 & 코드 ]

priority_queue를 이용한 Dijkstra

벨만 포드 알고리즘

[ 설명 ]

[ 로직 ]

[ 코드 ]

플로이드 워셜 알고리즘

[ 설명 ]

[ 코드 ]

MST 알고리즘

크루스칼(Kruskal) 알고리즘

[ 필요 지식 ]

[ 설명 ]

[ 코드 ]

프림(Prim) 알고리즘

개념

로직

크루스칼(Kruskal) 알고리즘과 차이점

이진 탐색

[ 설명 ]

[ 코드 - 반복문을 통한 이진탐색 구현 ]

이분매칭 알고리즘

[ 설명 ]

[ 예시 코드 ]

DFS / BFS

[ DFS ]

[ BFS ]

[CS 정리] 자료 구조(Data Structure)

[CS 정리] 네트워크(Network)

0개의 댓글