멀쩡한 사각형
코드
[ 1차 시도 ]
#include <cmath> #include <iostream> #include <algorithm> #include <vector> using namespace std; vector<pair<int,int>> p; int dx[3] = {0, 1, 1}; int dy[3] = {1, 0, 1}; bool check(int x, int y){ pair<int ,int> tmp = {x,y}; return find(p.begin(), p.end(), tmp) != p.end() ? true : false; } long long solution(int w,int h) { long long answer = 0; // 1. 해당 직선보다 같거나 작은 위치에 포함된 좌표 구하기 double line = -h/(double)w; double value; for(int i=0;i<=h;i++) { for(int j=0;j<=w;j++) { value = line * j + h; if(value >= i){ p.push_back({j,i}); } } } // 2. 특정 점(x,y) 기준으로 길이가 1인 정사각형 만들 수 있는지 검사 for(int i=0;i<p.size();i++) { int cnt=0; for(int j=0;j<3;j++) { int newX = p[i].first + dx[j]; int newY = p[i].second + dy[j]; if(newX > w || newY > h) continue; if(check(newX, newY) == false) continue; cnt++; } if(cnt == 3) answer++; } return answer*2; }1) 해당 좌표중 그래프보다 같거나 작은 좌표들을
vector<pair<int,int>> p에 넣는다.
2)p에 있는 좌표들을 대상으로 사각형을 만들 수 있는지 검사한다!
: 해당 풀이로 답을 구할수는 있다. 하지만 이미 (1번)과정에서 O(N^2)의 시간복잡도로 시간초과 ㅠㅠ
(기울기를 구할 때 -h/w로 했지만, 나누는 수인 w에double처리를 안해주는 바보같은행동을함..)
[ 2차시도 ]
#include <cmath> #include <iostream> #include <algorithm> #include <vector> using namespace std; long long solution(int w,int h) { long long answer = 0; for(int i=1;i<=w;i++) { for(int j=1;j<=h;j++) { if(h*i + w*j <= h*w) answer++; } } return answer*2; }
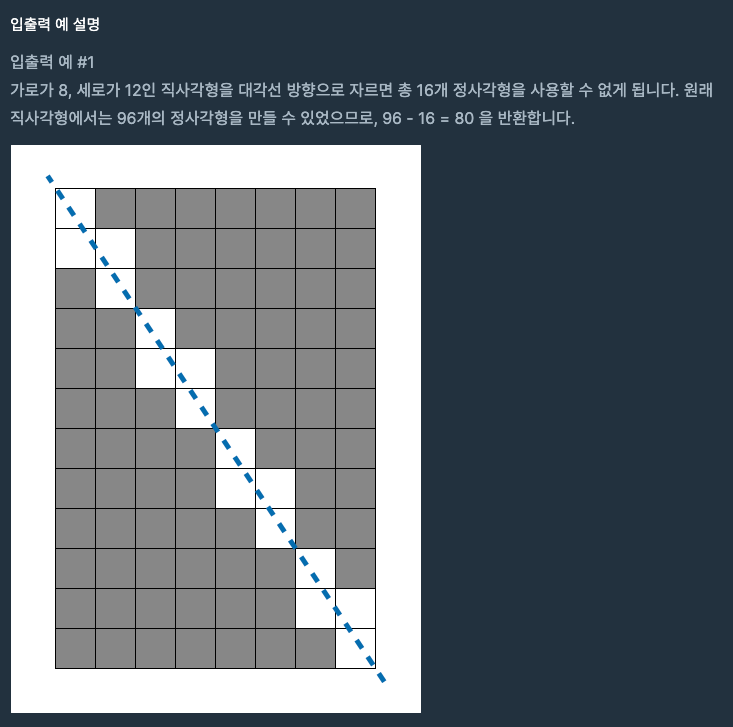
- 해당 그림에서 x나y가 0인 좌표는 사실상 길이가 1인 사각형을 구하는데 필요가 없다
--> x와 y를 1부터 해당 길이까지 범위 설정을 한다h*x + w*y <= h*w라는 식에 만족한다면 직선아래에 있는 좌표임을 알 수 있다!- 해당하는 개수를 구하면 길이가 1인 사각형의 개수를 구할 수 있다!
- 여전히 x와 y의 거의 모든 좌표를 검사해야하기 때문에
O(N^2)라서 시간초과가 뜬다.
[ 최종 답안(1) ]
#include <cmath> #include <iostream> #include <algorithm> #include <vector> using namespace std; long long solution(int w,int h) { long long answer = 0; int gcb; int a = max(w,h); int b = min(w,h); int c ; while(b != 0){ c = a%b; a = b; b = c; } gcb = a; return ((long)w * (long)h) - ((long)w + (long)h -a); }
- 해당 문제는 시간초과 때문에 결국 규칙을 찾는 문제인걸 깨달았다.
- 빠지는 사각형의 개수를 나열하며 규칙을 찾아야 한다.
2x3 =(2x3)+(2+3-gcb)/4x6=(4x6)+(4+6-gcb)가 규칙이다!- 결국 최대공약수(gcb)를 구해서 해당 규칙에 적용하면 된다. (유클리드 호제법 사용!)
- 이런 규칙을 찾을 때에
최대공약수의 쓰임이 많다고 하니 알아두자
[ 최종 답안(2) - best ]
#include <cmath> #include <iostream> #include <algorithm> #include <vector> #include <cmath> using namespace std; long long solution(int w,int h) { long long answer = 0; if(w == h){ return (long)w * (long)w - w; } int small = min(w,h); int large = max(w,h); for(int i=1;i<small;i++) { int he = (long)large * i/(long)small; answer += he; } return answer*2; }
- 2차시도 에서는 사각형의 넓이를 하나씩 추가해서 시간복잡도가 O(N^2)가되어 시간초과가 떴다.
- 굳이 그렇게 하지 않고, 1~w-1까지 길이에 바로 직선에 대입해 내림처리한 크기의 사각형을 가질 수 있다는 사실!
- int자료형으로 커버할 수 없기 때문에 long 자료형을 이용함!