소수 찾기
- 일반적인 방법으로 소수를 찾으면 O(N^2)의 시간복잡도를 가져서 시간초과가 나온다.
- 즉,
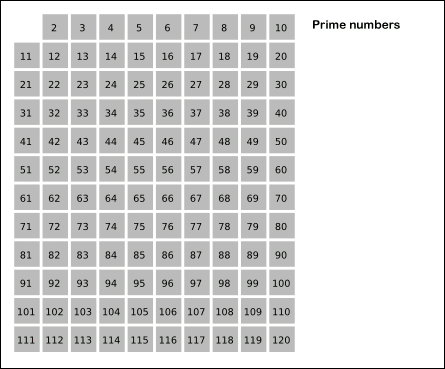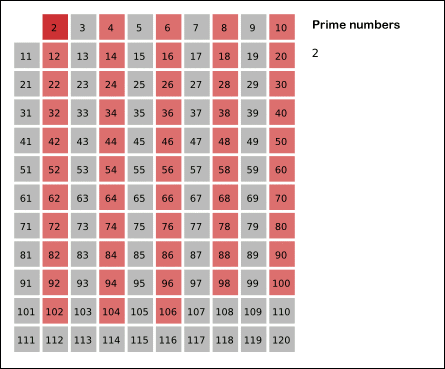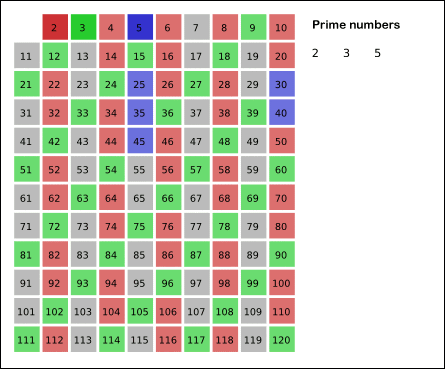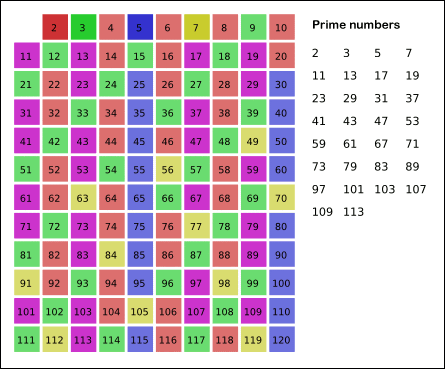
에라토스테네스의 채를 사용해서 O(N*logN)의 시간복잡도를 유지해야만 성공할 수 있다.- [ 에라토스테네스의 채 원리 ]
: 어떤 수의 배수가 되는 수는 소수가 될 수 없기에 미리 false처리를 해준다
코드
#include <string> #include <vector> using namespace std; int solution(int n) { int answer = 0; /* 에라토스테네스의 체 - 소수를 O(NlogN)으로 구하는 과정 */ vector<bool> v(n+1, true); // 2부터 n까지 배수에 해당하면 본인 빼고 다 false로 체크 후 개수 cnt for(int i=2;i<n+1;i++) { if(v[i] == true) { for (int j=2; i*j<n+1; j++) v[i*j] = false; answer++; } } return answer; }