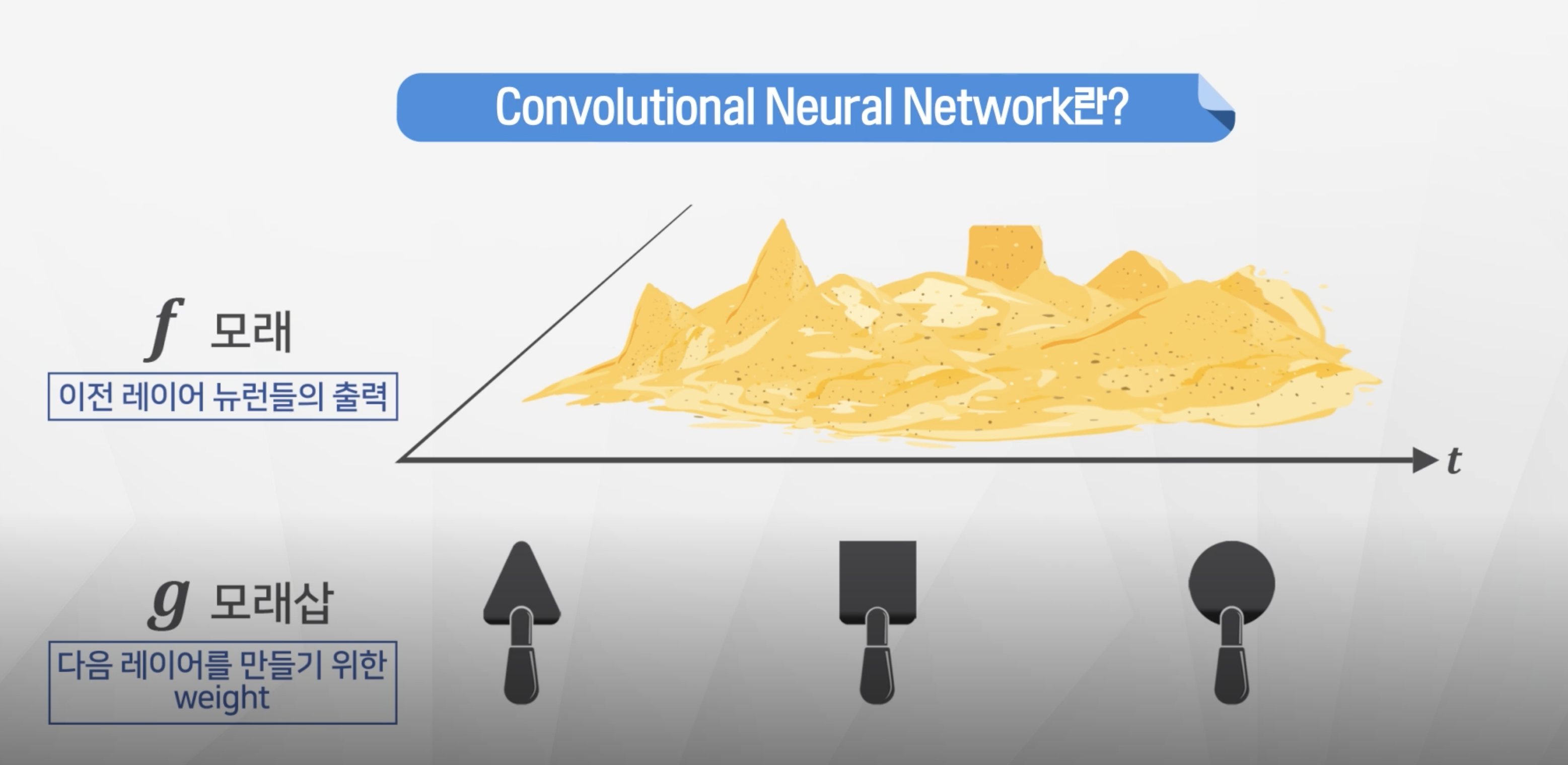
CNN : Convolutional Neural Network 합성곱 신경망

합성곱(convolution)의 개념

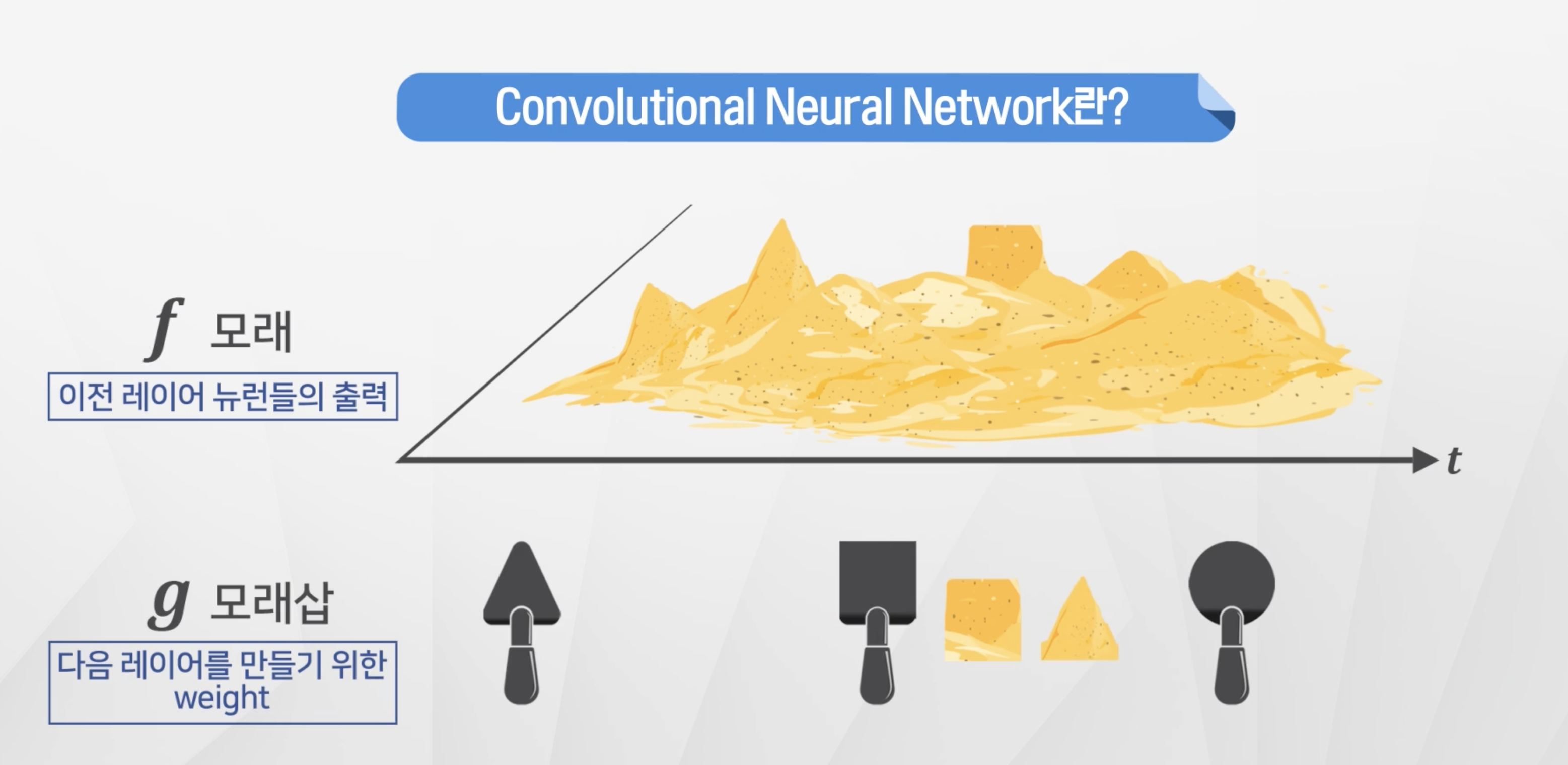
• 전체 모래에서 원하는 필터를 적용해서 데이터를 가져온다.
• 필터를 적용한다 = 행렬곱을 적용한다.

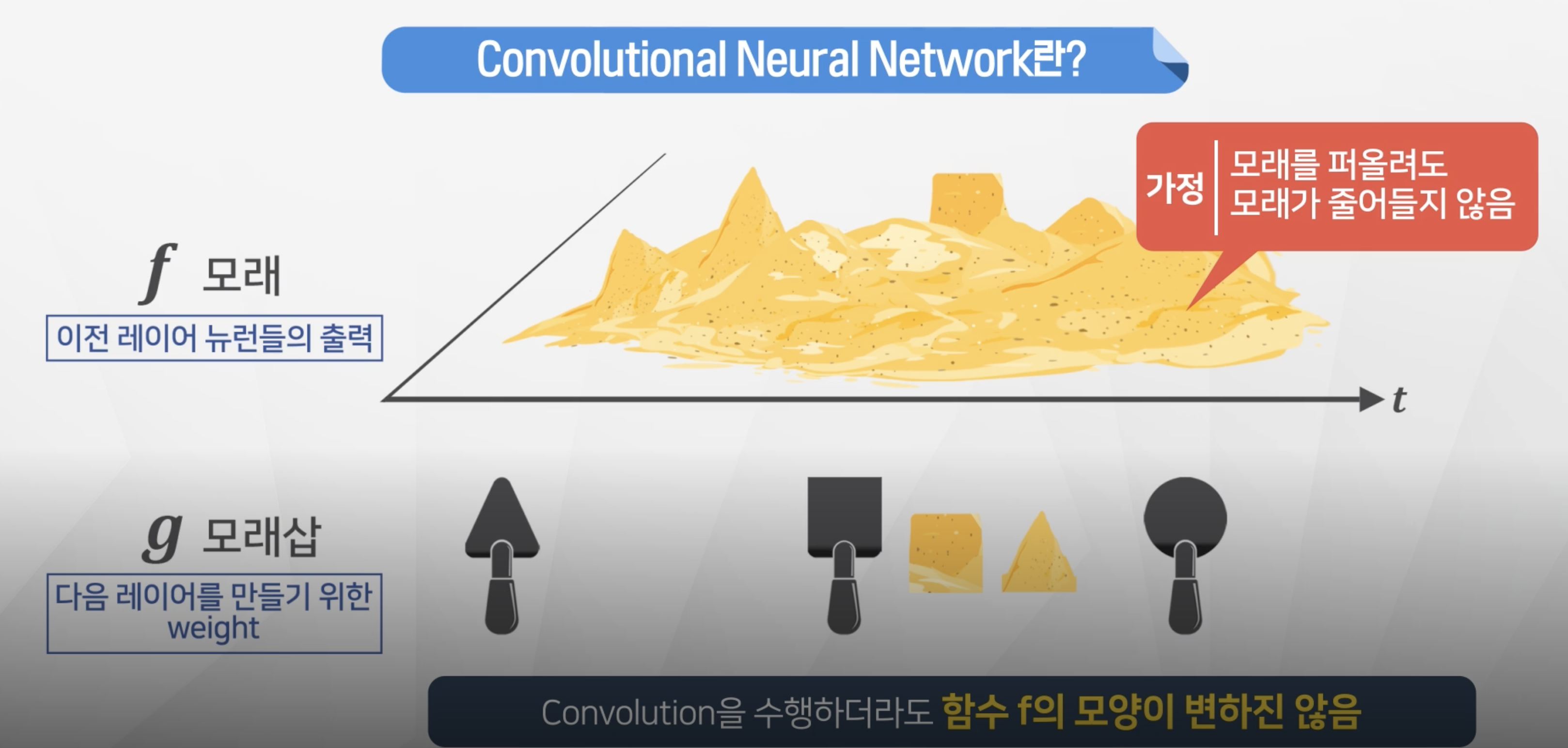
• 원래 f는 변하지 않는다!

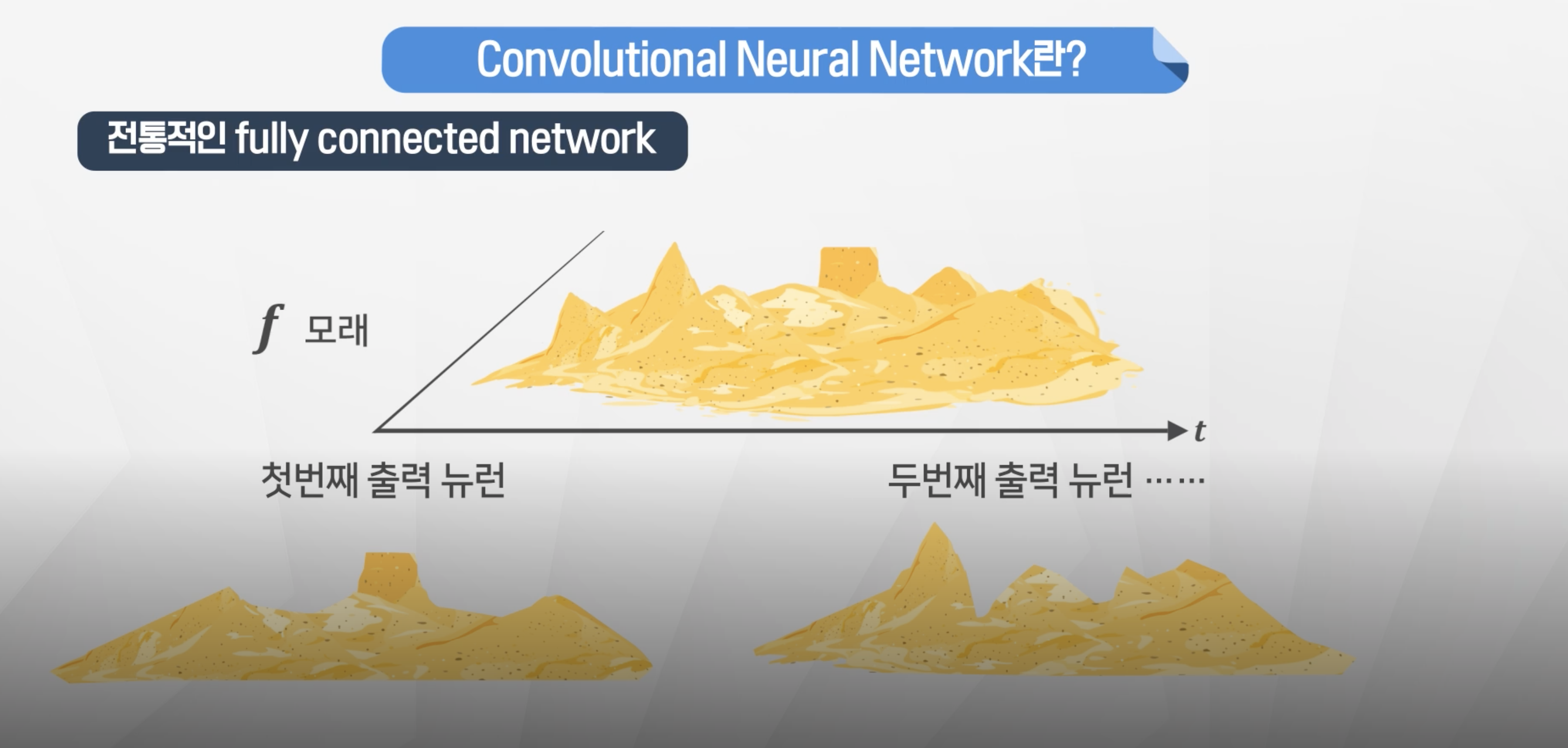
• 전통적인 fully-connected Network같은 경우 각 노드에게 모두 가중치가 부여되어있기 떄문에 삽의 모양이 전체 모래 모양과 동일한 형태의 가중치로 계산

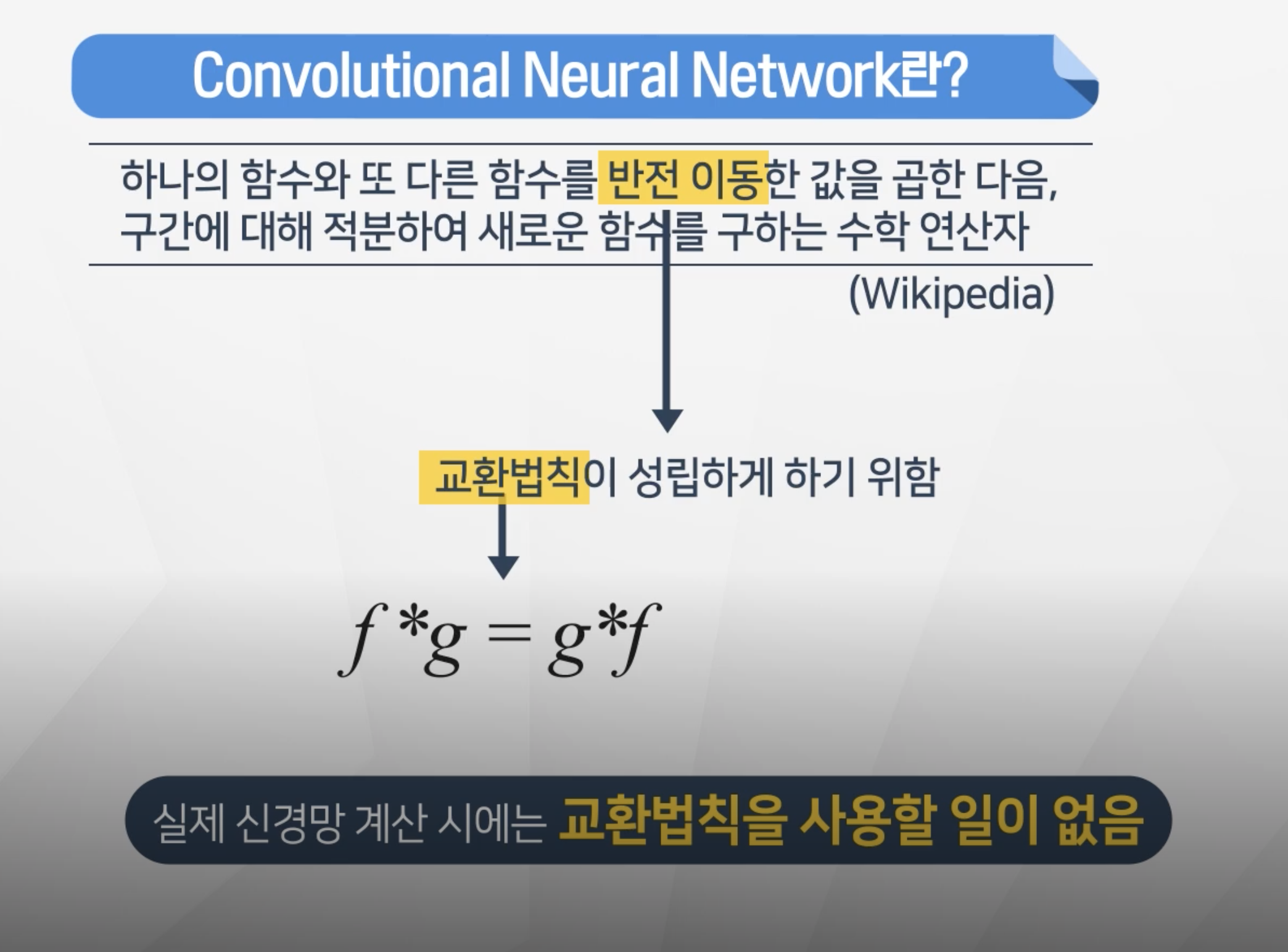
• 기본 수학 개념으로서의 합성곱은 교환법칙이 성립하기 위해서 반전 이동이 필요한데 실제 신경망 계산 시에는 교환볍칙을 사용할 일이 없어서 반전이동도 하지 않는다.

1차원 합성곱

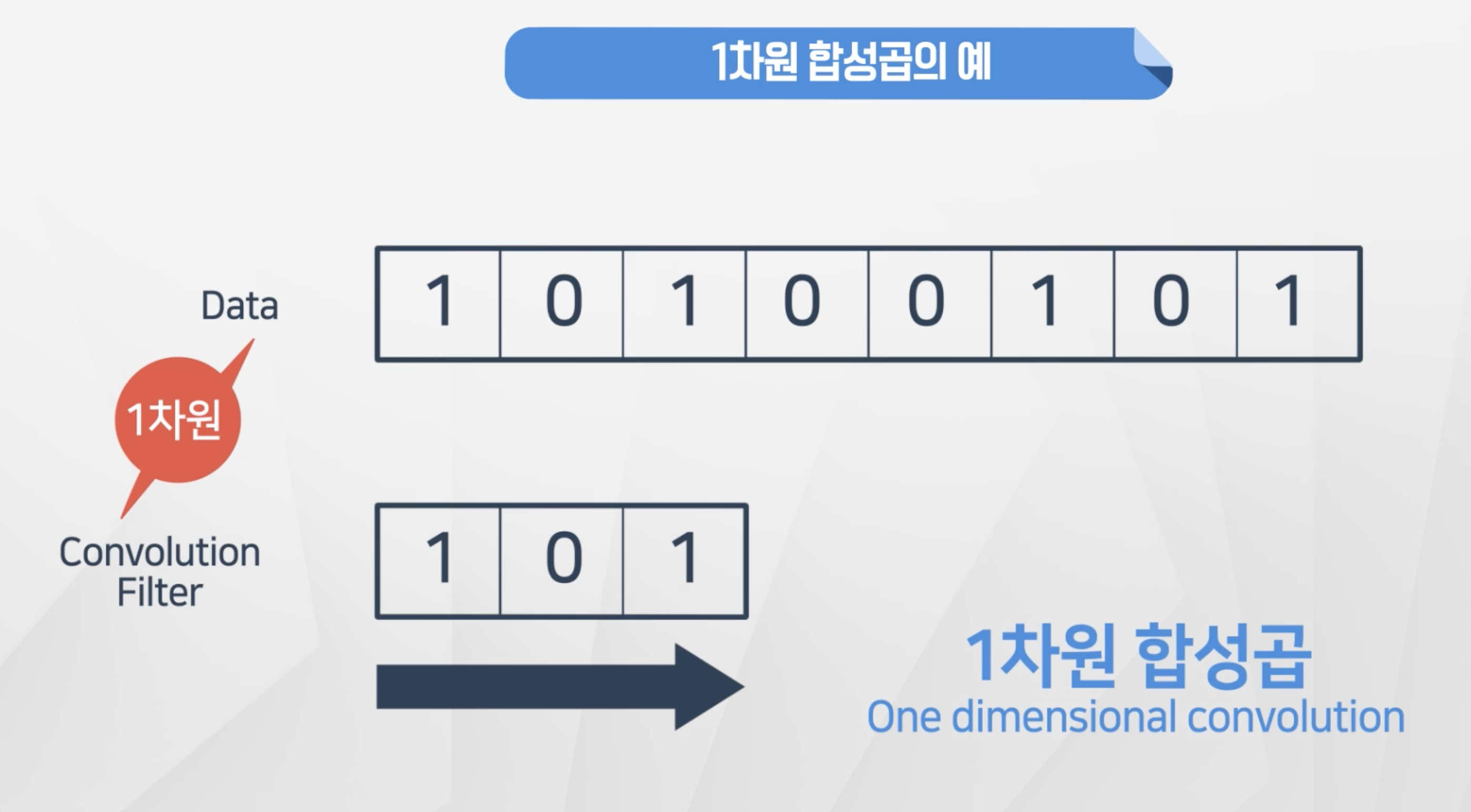
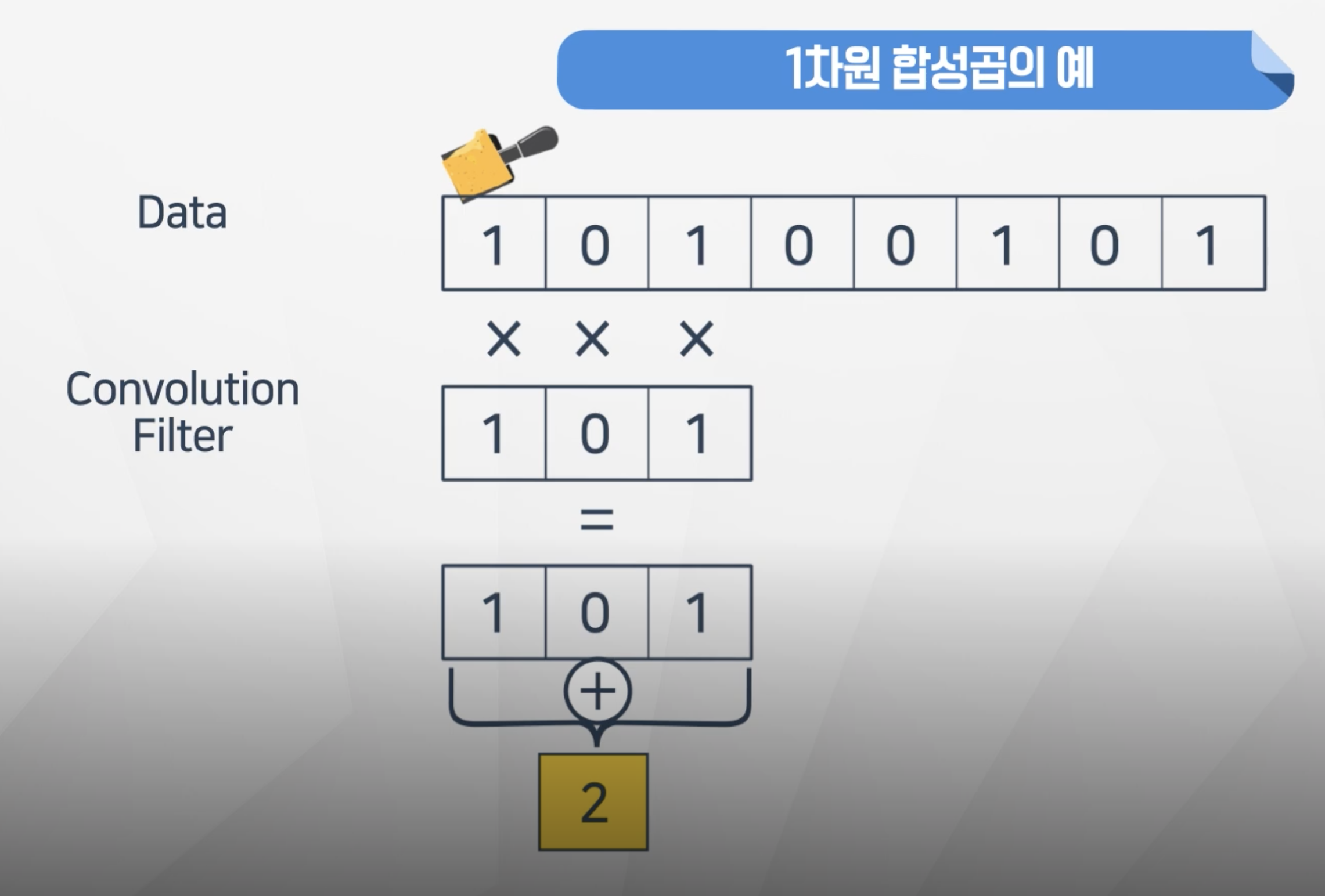
• 1차원 합성곱은 Convolution Filter를 Data에 곱해서 나온 값을 다른 행렬로 정리

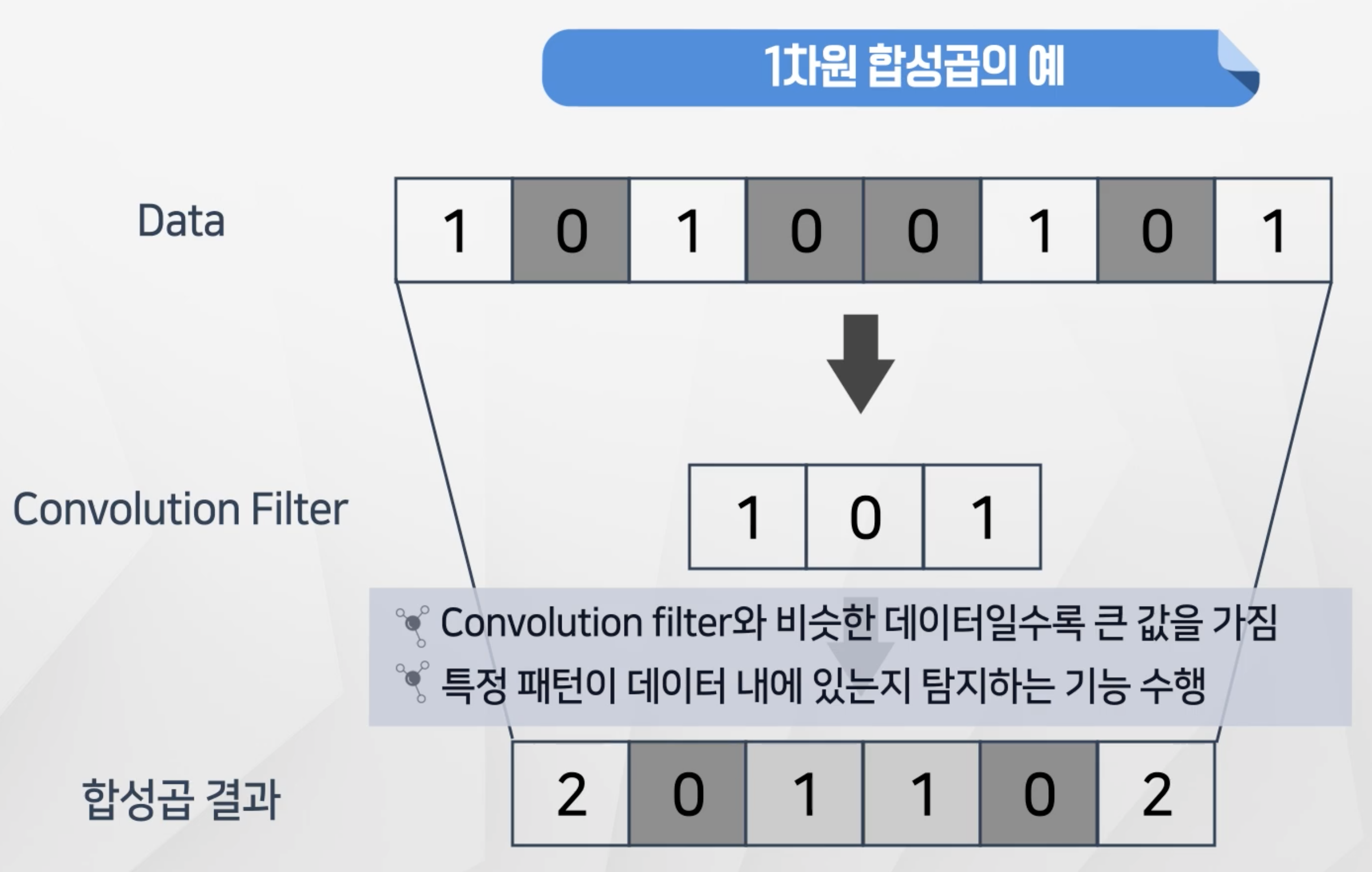
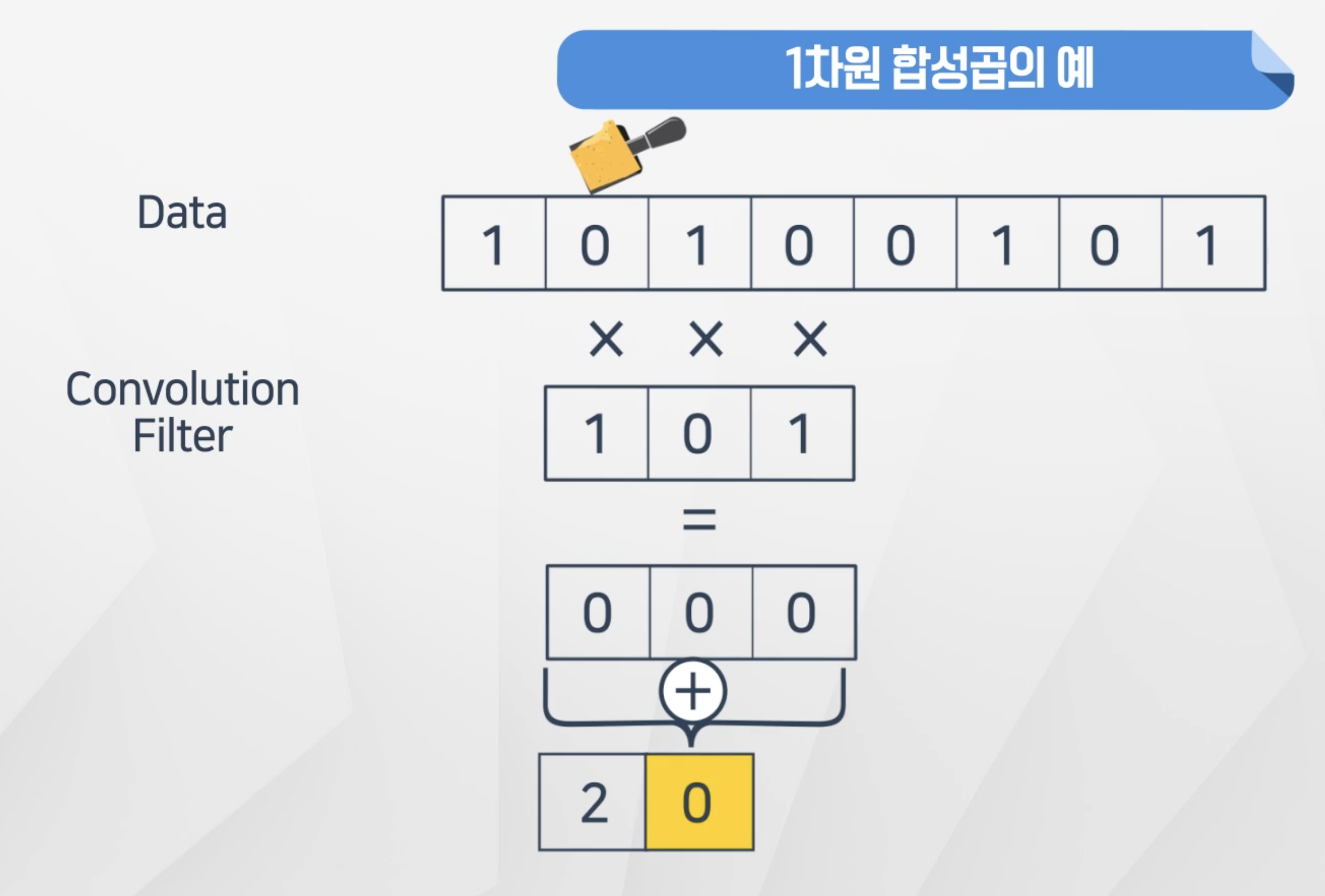
• 위에 필터와 일치하는 1 0 1의 경우의 값이 가장 큰 합성곱결과를 가지는 것을 확인할 수 있음
• 이 떄 원래 데이터가 1 -1 1인 경우에도 필터를 곱하면 똑같이 가장 큰 값인 2가 되는 것을 확인할 수 있음

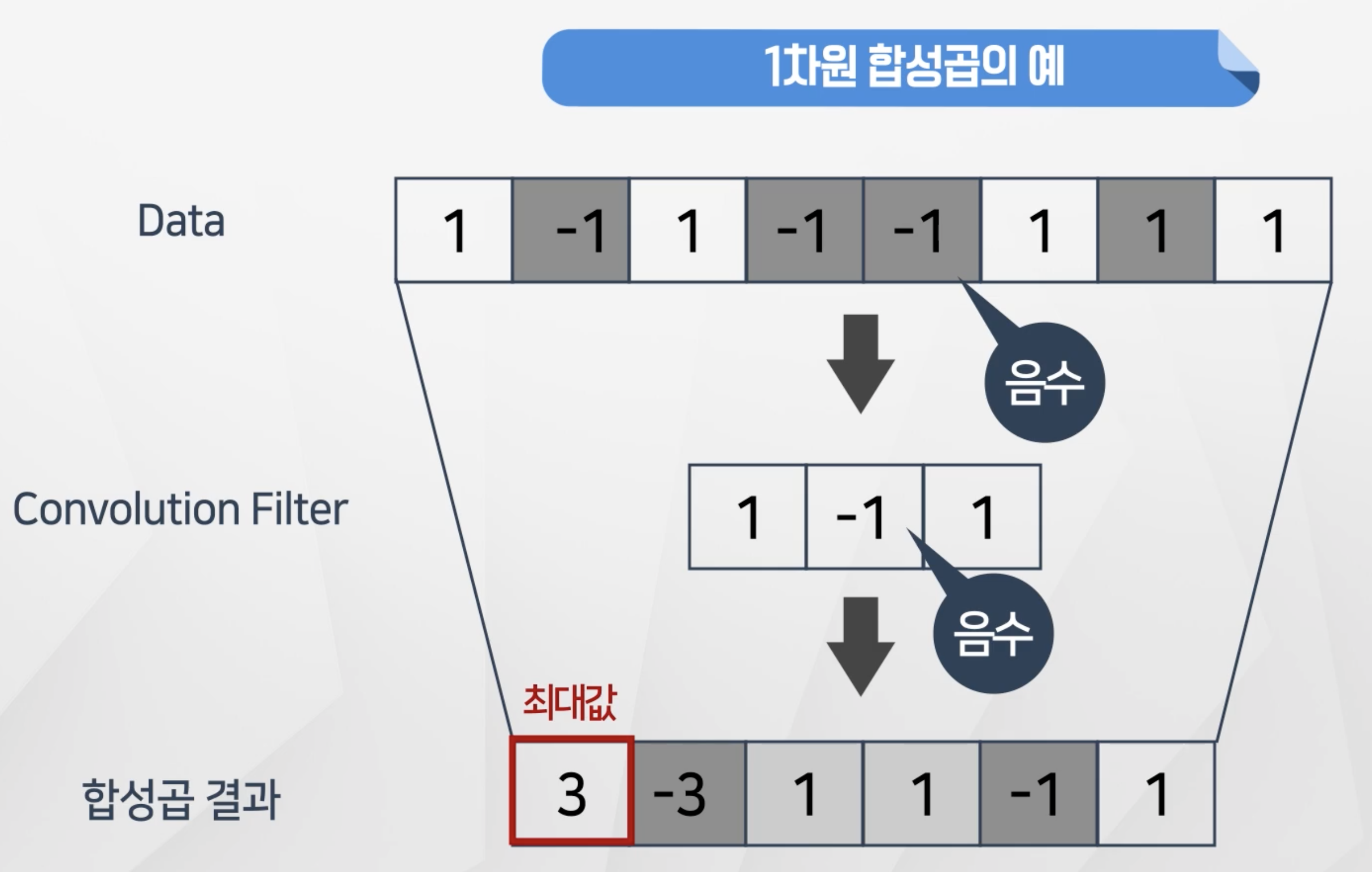
• 이런 경우를 방지하기 위해서 필터에 data filter에 음수값이 들어갈 수 있음
• 이렇게 하면 정확히 일치하는 경우만 값이 가장 크게 만들 수 있음

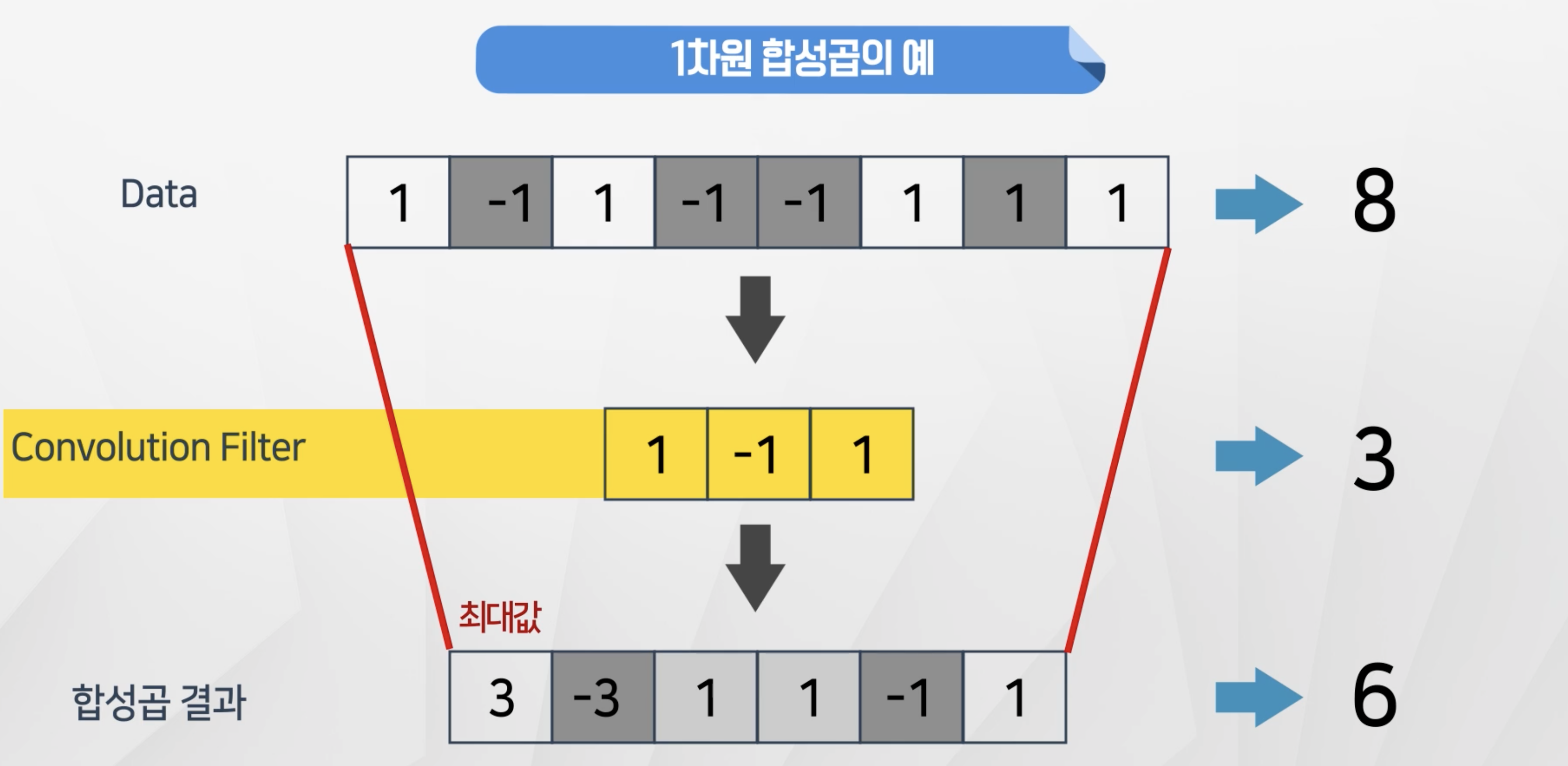
• 필터를 적용하게 되면 원래 데이터보다 크기가 작아진다.
• 8개의 데이터를 크기 3인 필터를 적용을 하니 6으로 줄어들었음

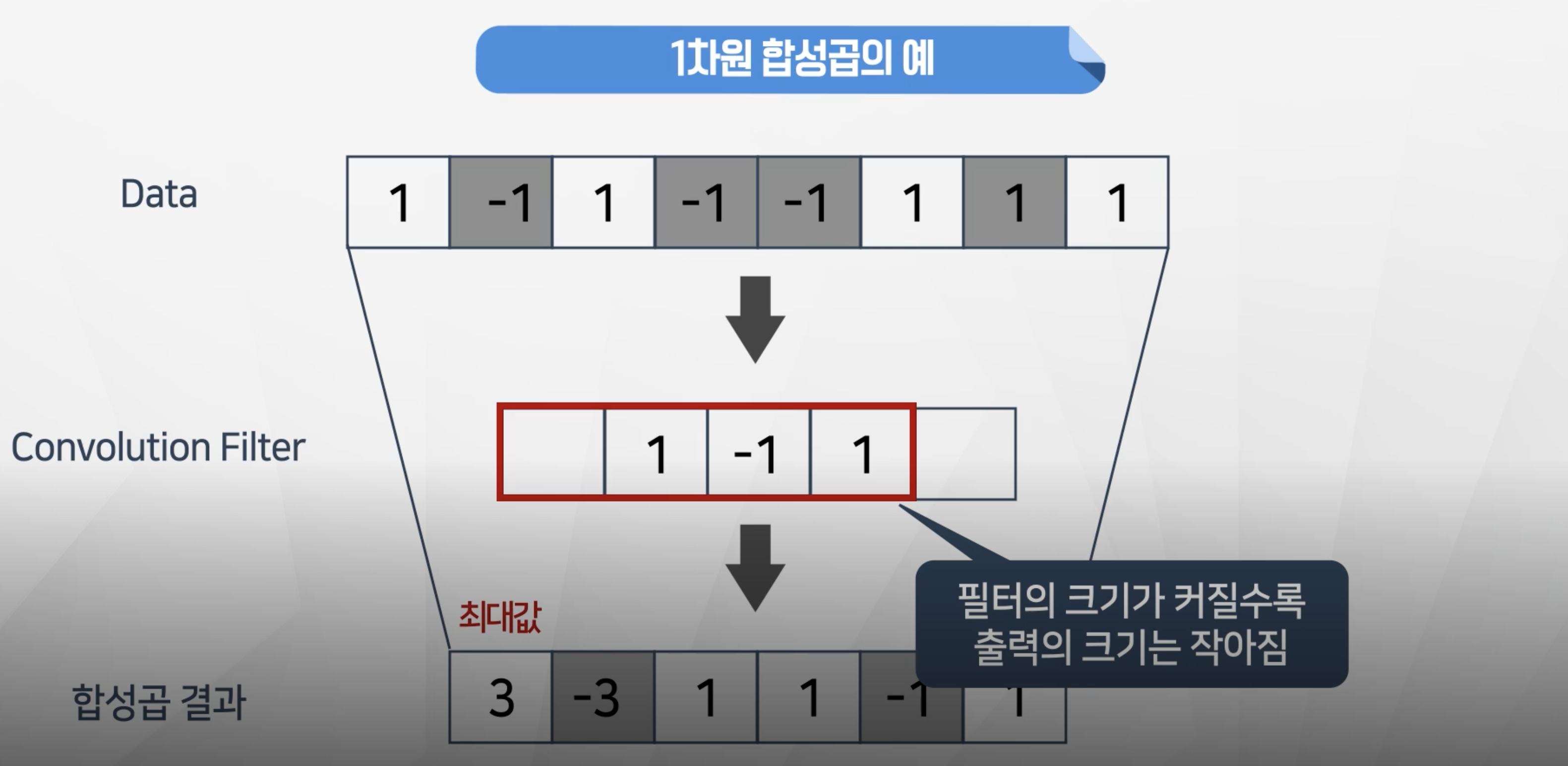
• 필터의 크기가 커질수록 출력의 크기는 작아진다.
• 필터의 크기가 4인 경우는 5개로 줄어든다.

2차원 합성곱

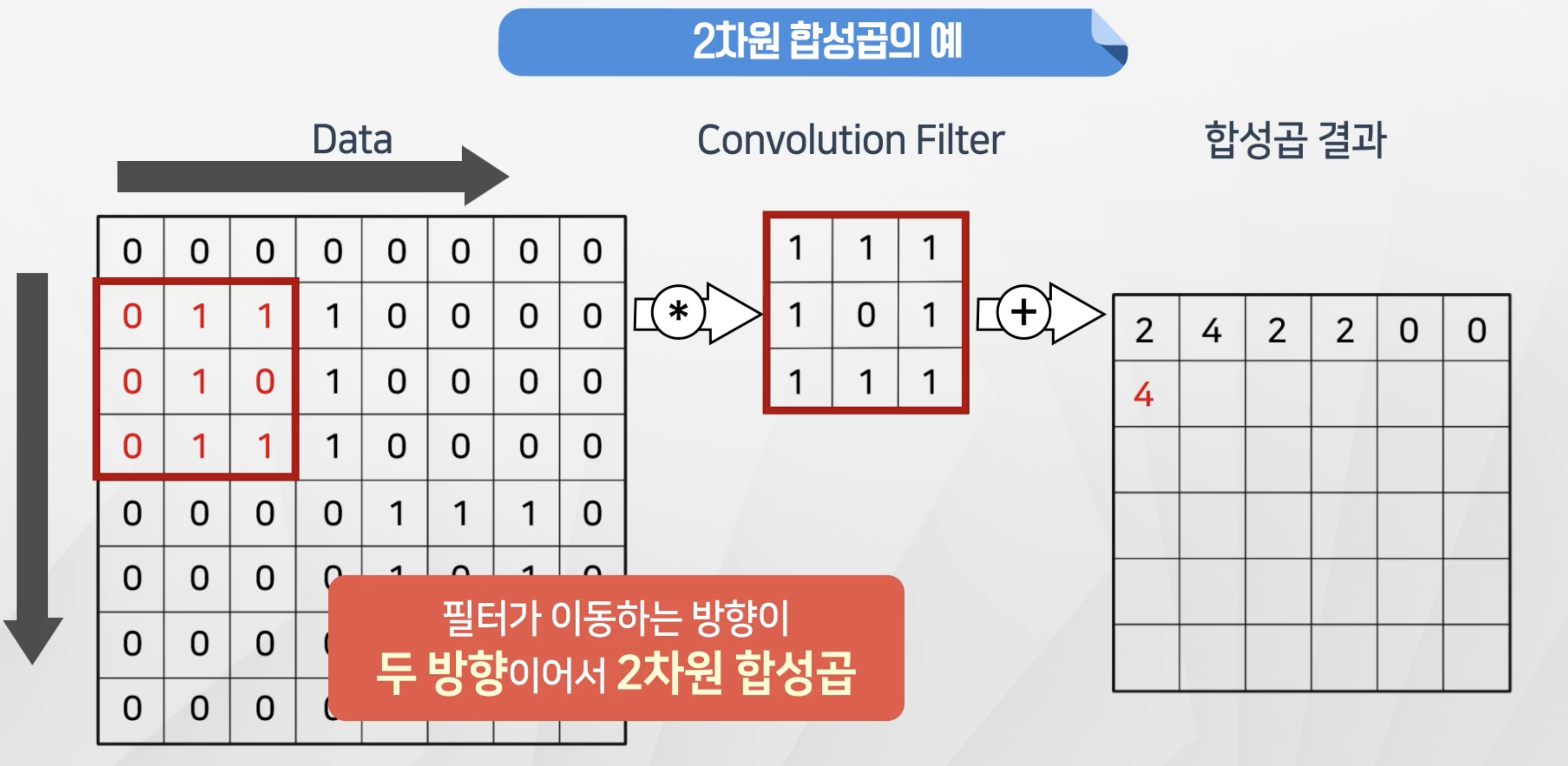
• 2차원 합성곱은 필터가 가로,세로방향으로 두방향으로 이동하는 합성곱이다.
  
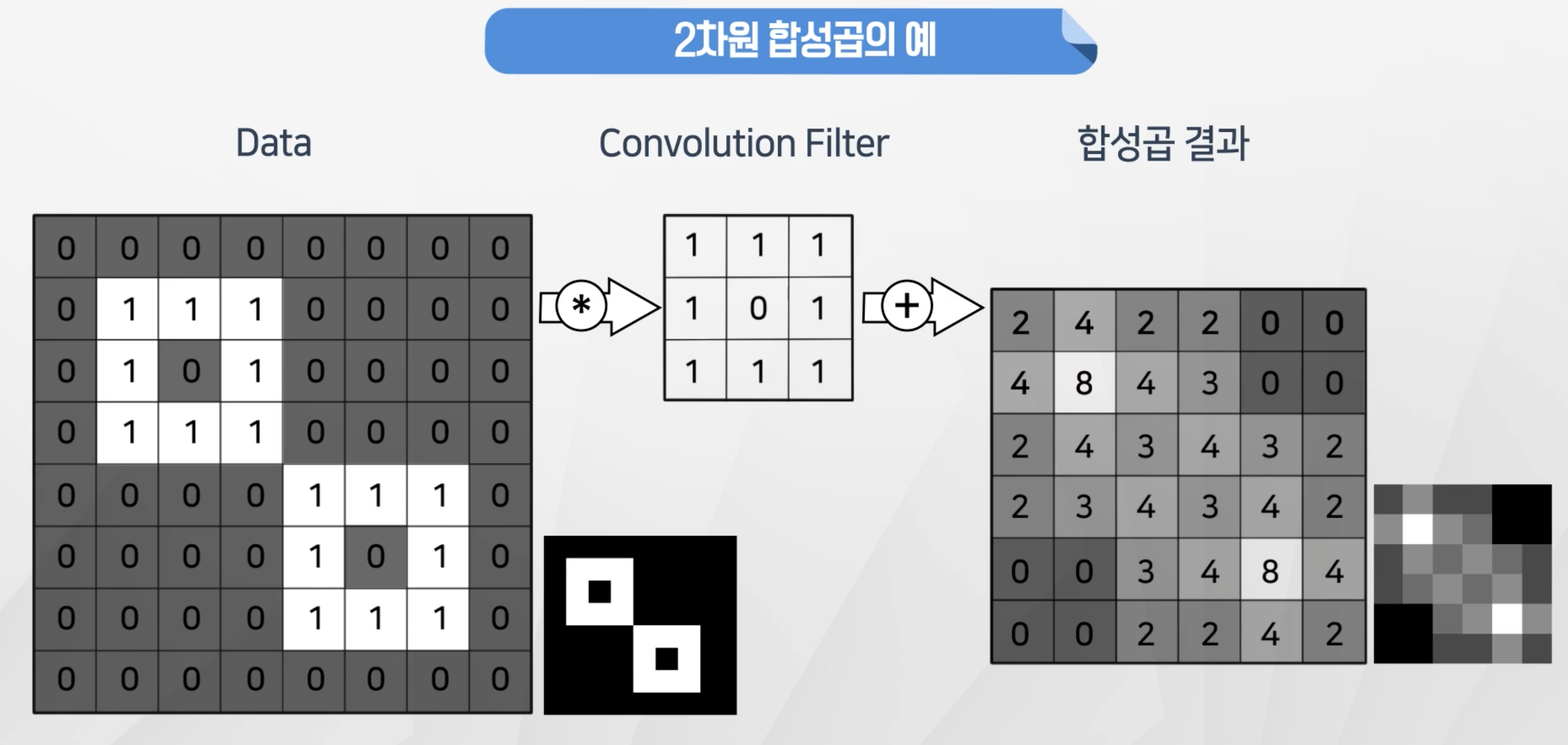
• 합성곱을 한 결과를 히트맵으로 표현을 하면 패턴이 일치하는 부분이 더 밝은 색으로 표시되는 것을 확인할 수 있다.

Stride

• 합성곱이 움직이는 step의 크기를 나타냄

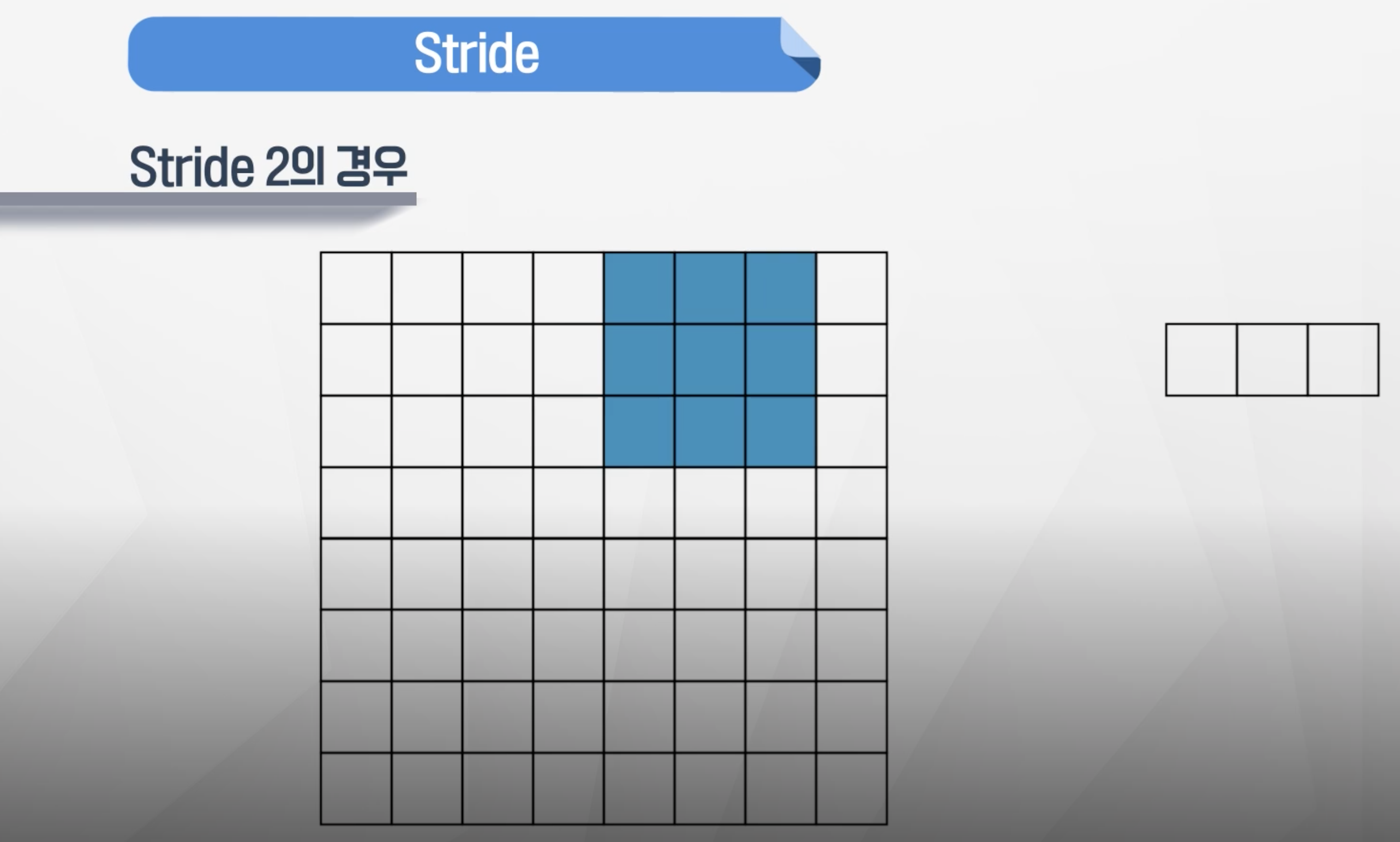
• stride2씩 가다가 2칸 기준으로는 더 움직일 수 없음
  
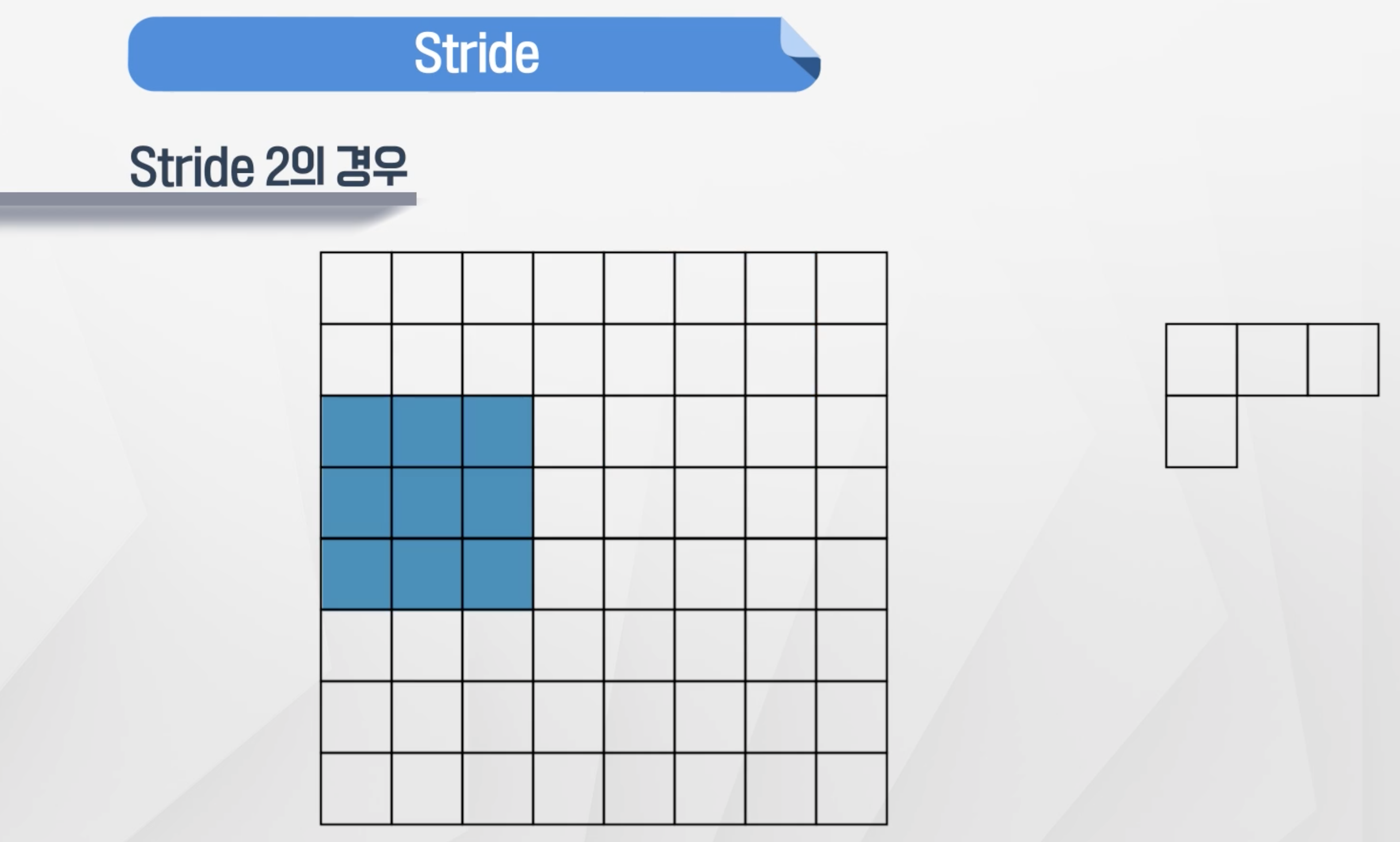
• 이런 경우 다음 행에서 합성곱을 진행

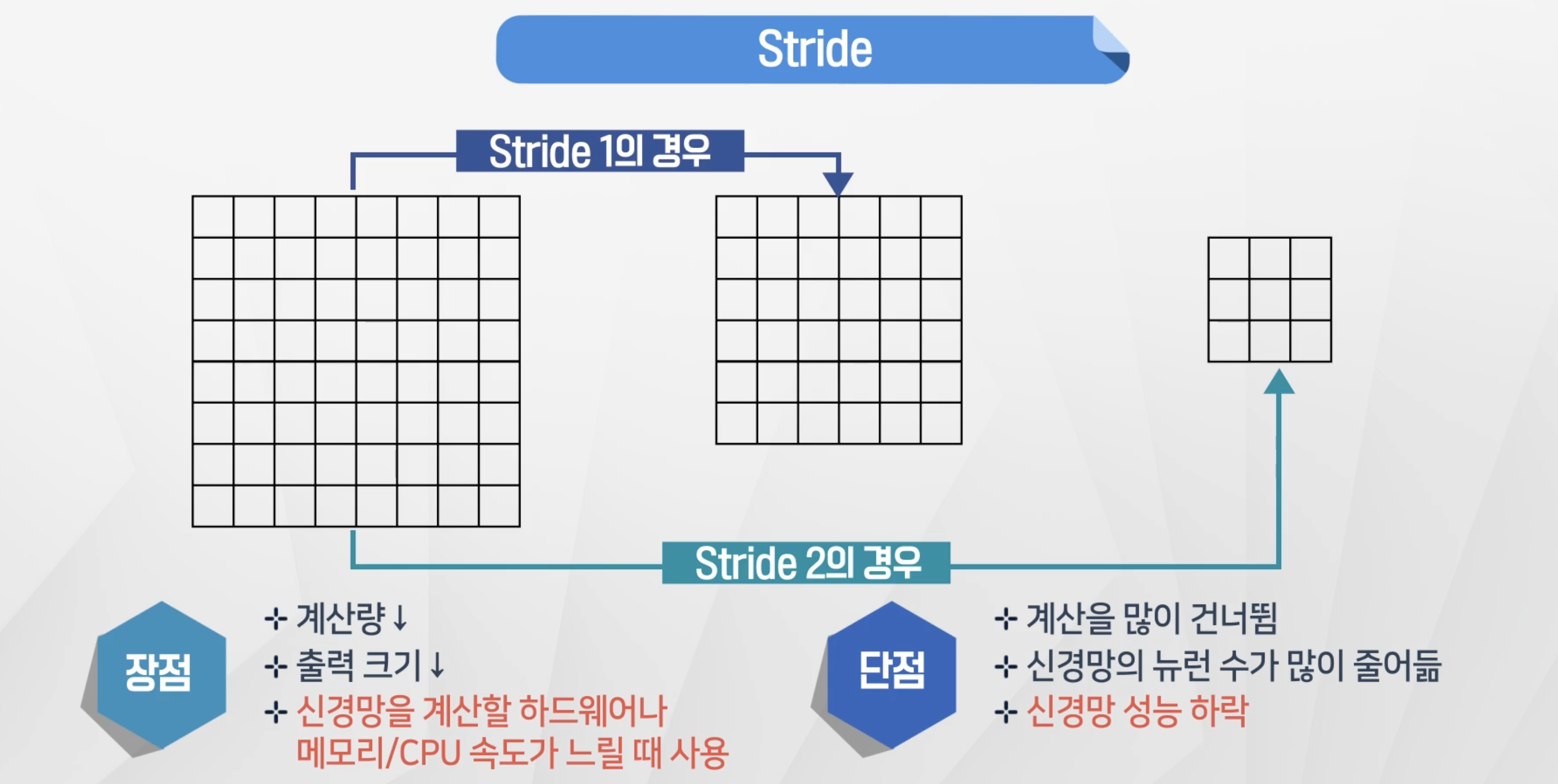
• stride를 크게 적용을 하게 되면 계산 크기가 줄어들게 되어 사양이 낮은 경우 적용
• 단 계산을 건너뛰기 때문에 신경만 성능이 하락하게 된다.

Zero-Padding

• 필터는 원래 데이터보다 작게 설정을 하기 떄문에 결과 데이터 크기가 원데이터에 비해서 작아짐
• 이를 방지하기 위해서 원데이터 가장자리에 0을 추가
  
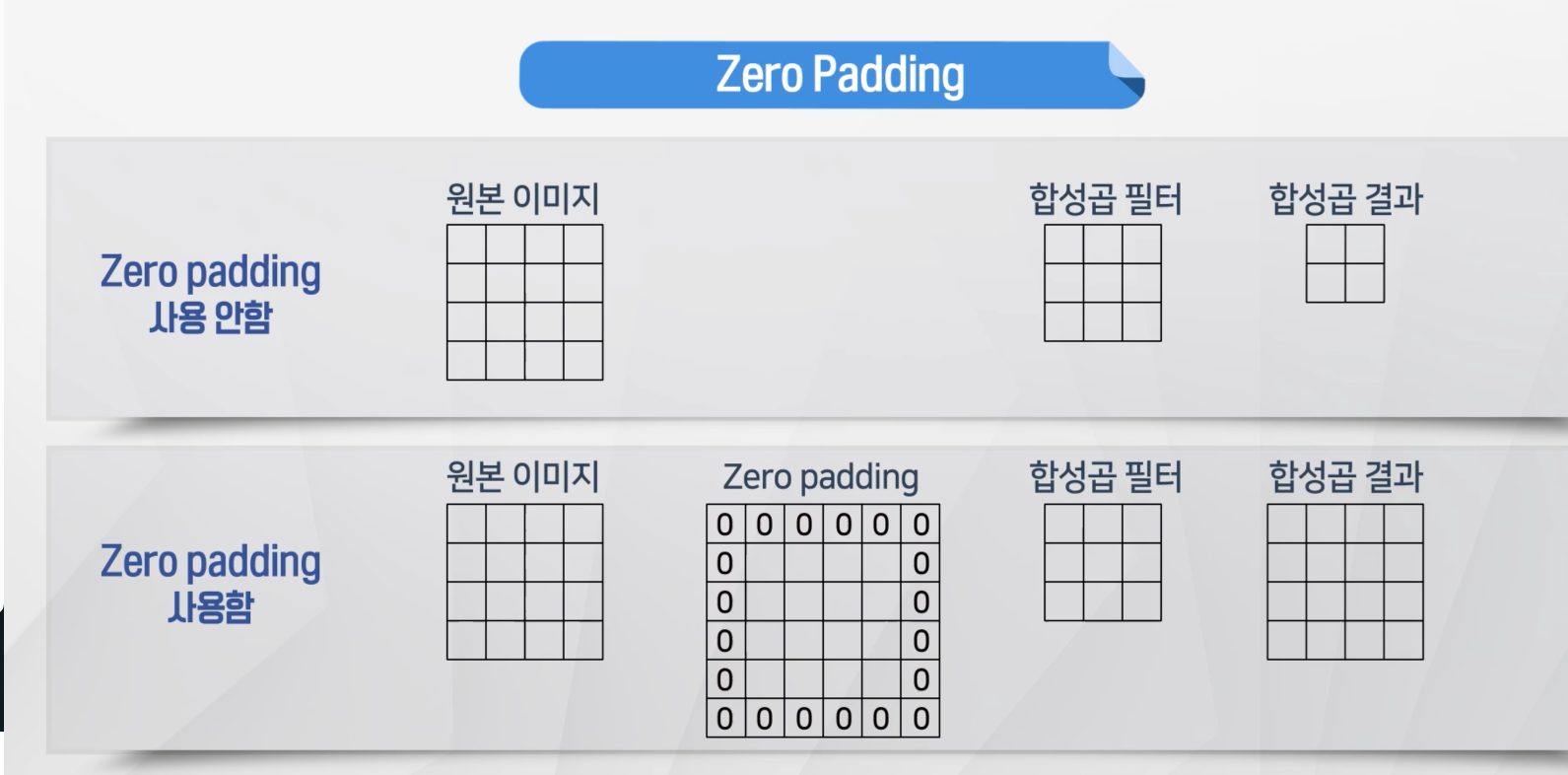
• 0을 가장자리에 추가를 한 경우 원본 이미지와 합성곱 결과가 동일한 것을 확인 가능

합성곱 신경망의 장점

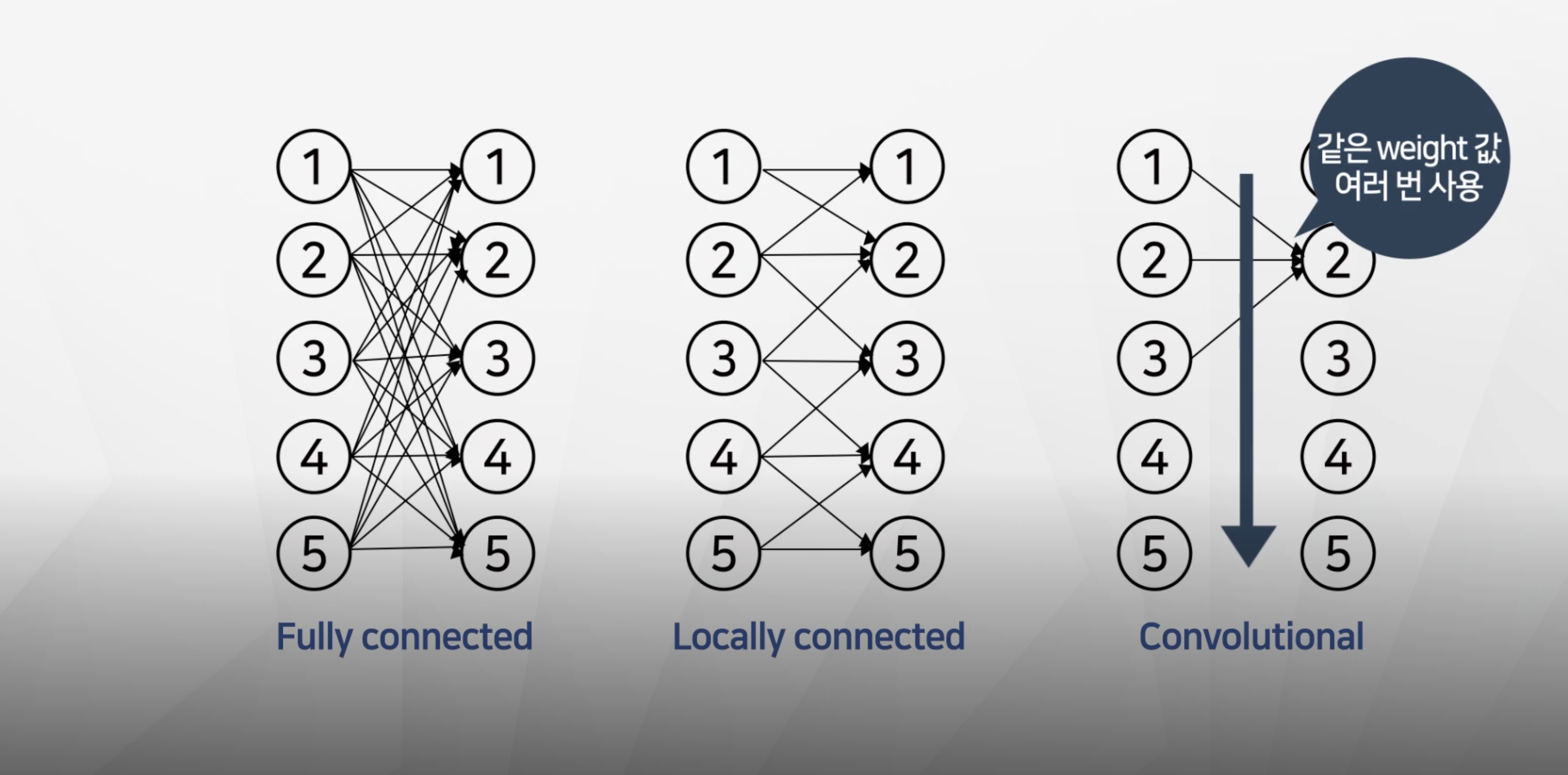
• 동일한 필터(weight)를 각 노드에 대해서 적용을 한다.
  

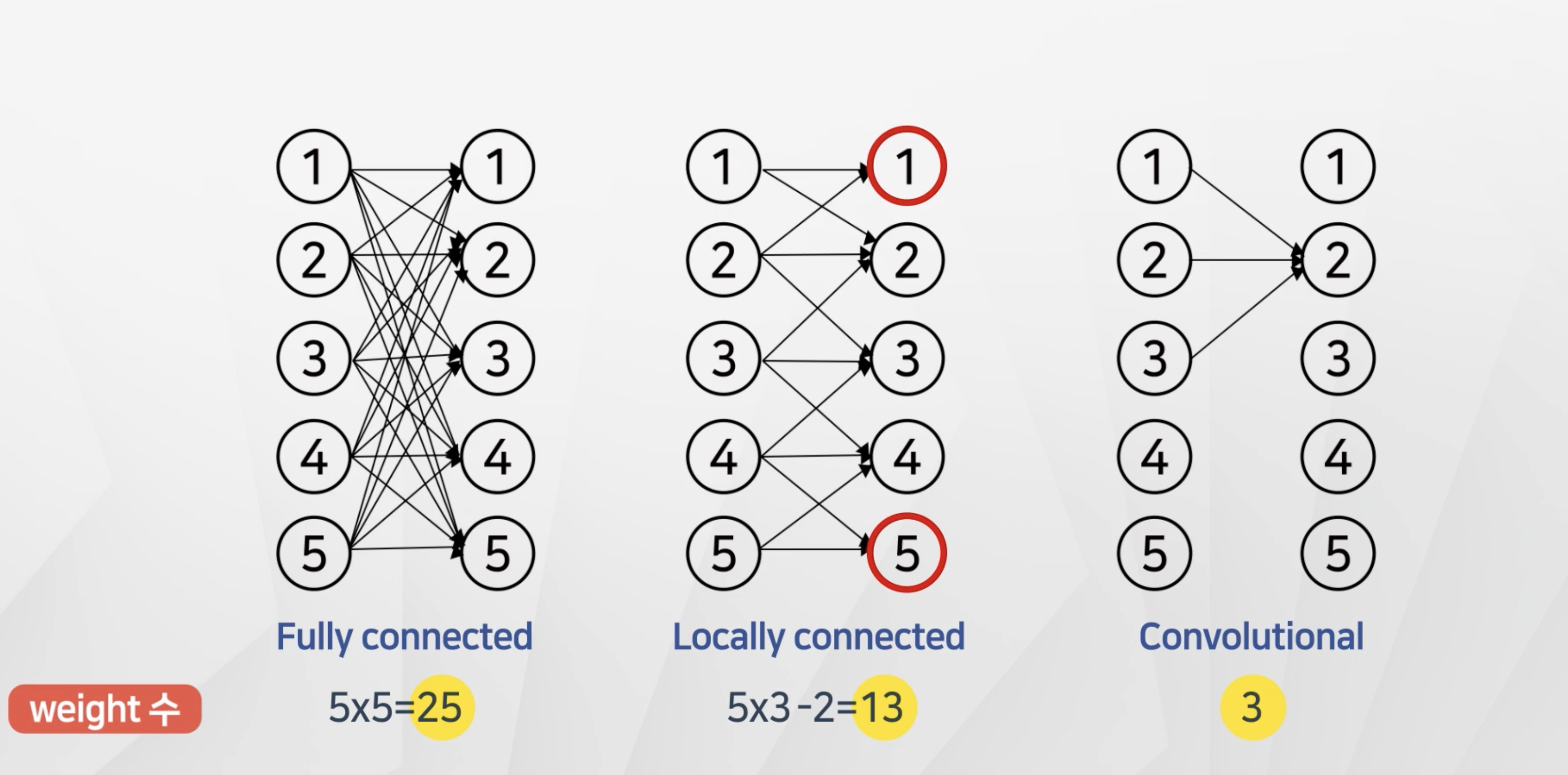
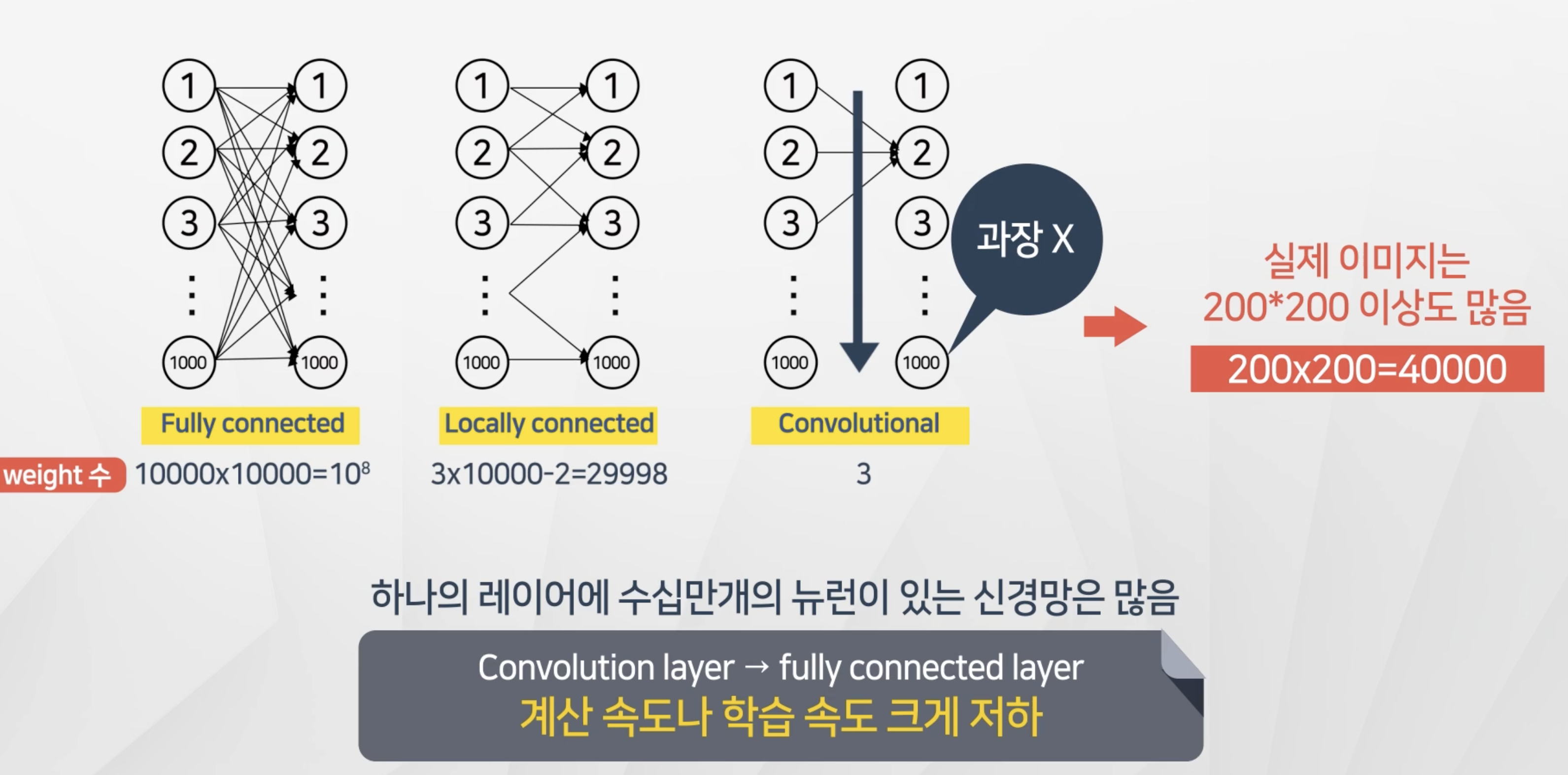
• 그래서 가중치의 갯수가 fully-connected-network와 비교해서 크게 줄어든다.

합성곱 신경망의 생물학적 근거

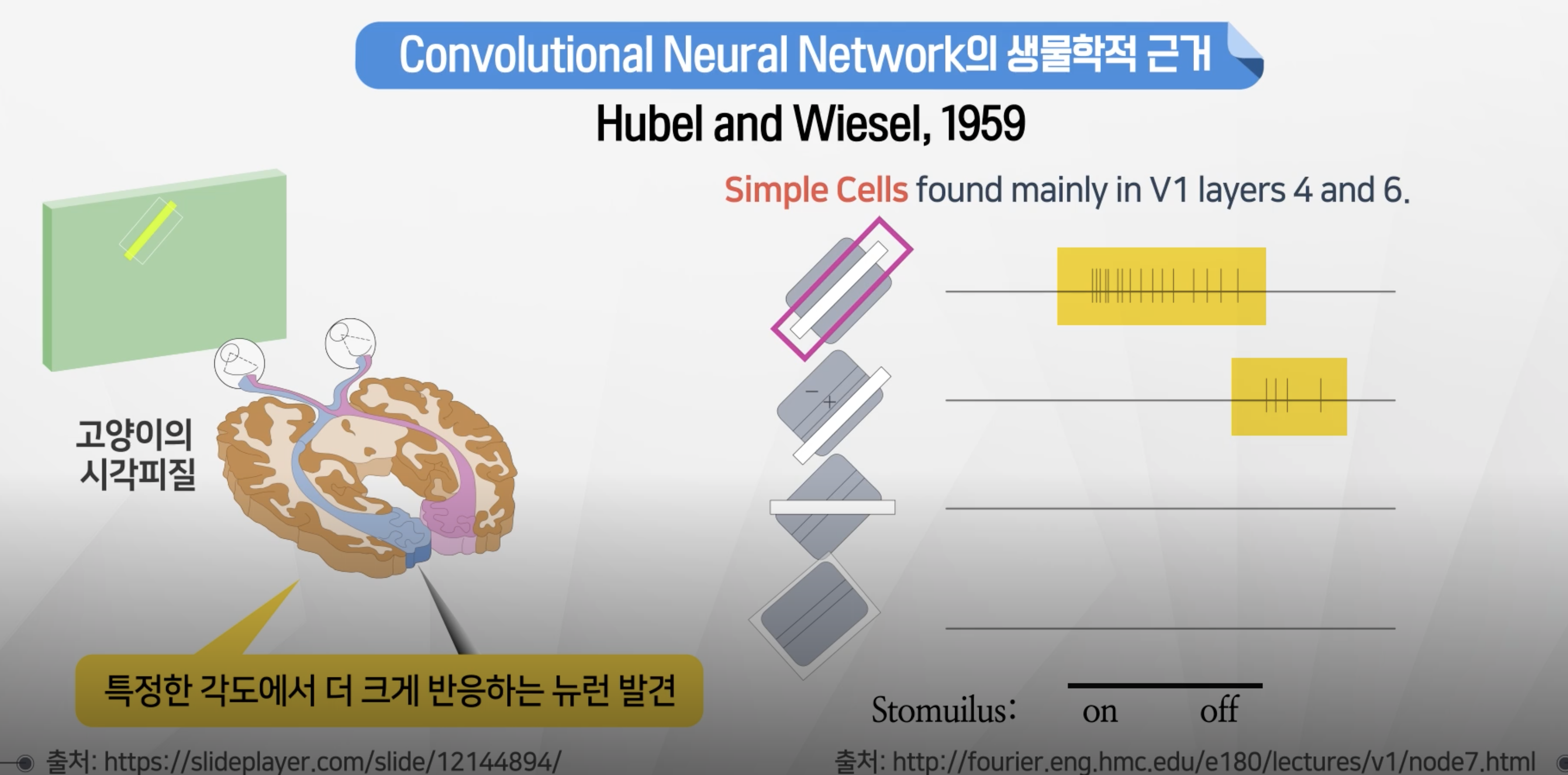
• 시각적으로 패턴을 인지하는 과정이 존재
• 특정 패턴으로 일치하는 경우 뉴런이 더 반응
  
  
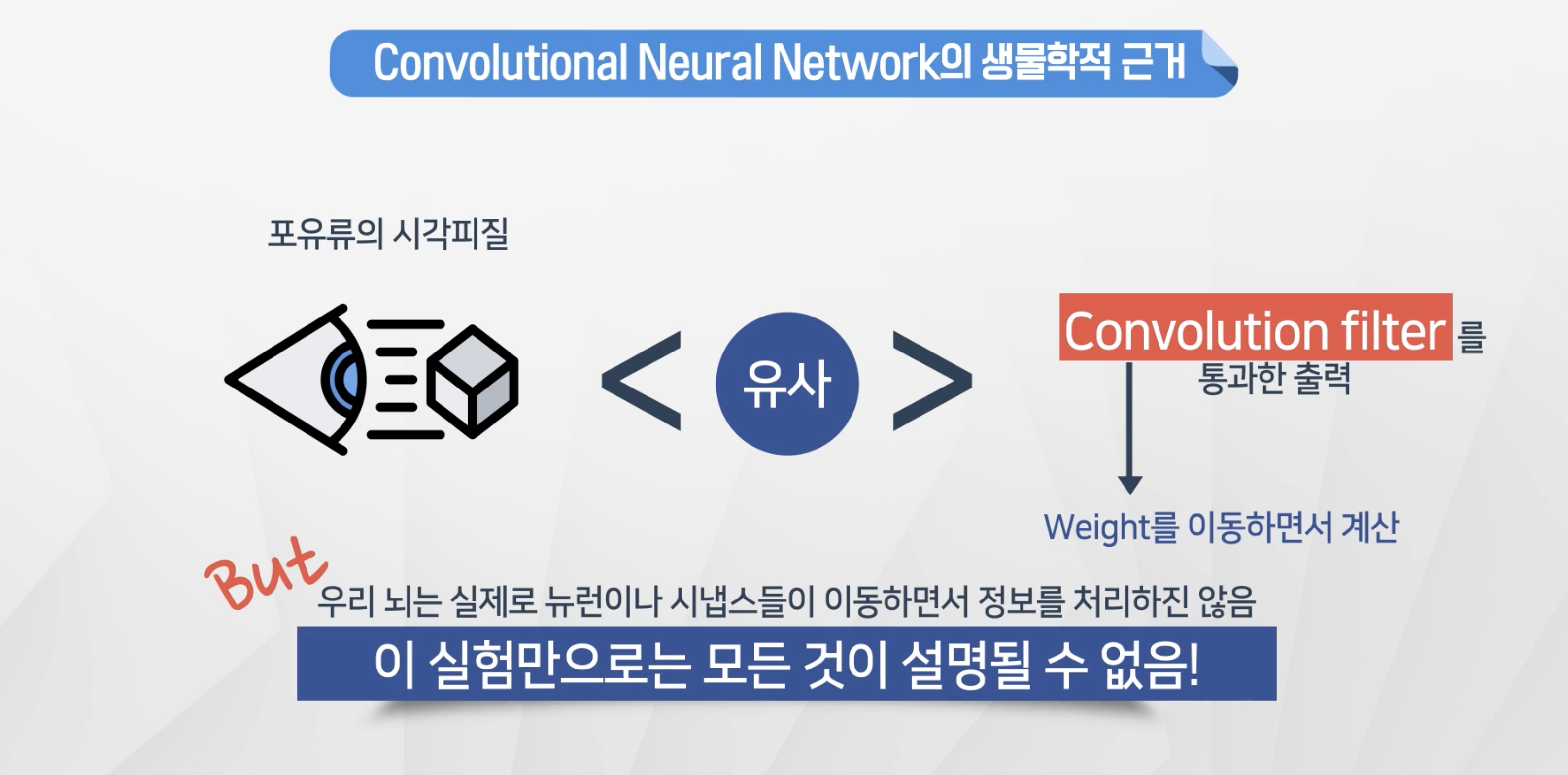
• 합성곱 신경망으로 이미지 패턴을 인식하는 것이 시각정보를 처리하는 뉴런과 비슷

Apply multi-layer CNN

• layer1 : 명암만 인식
• layer2 : 곡선, 형태 등을 인식
• layer3 : 좀 더 복잡한 형태를 인식
• layer4 : 사람 얼굴을 구분 등
• 깊은 구조의 신경망일수록 이미지 인식 성능이 더 좋아진다.

simple NN과 CNN비교

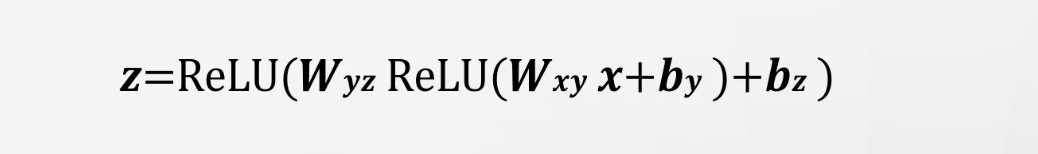
• 이와같은 2층의 신경망모델에 CNN을 적용을 하면 다음과 같다.

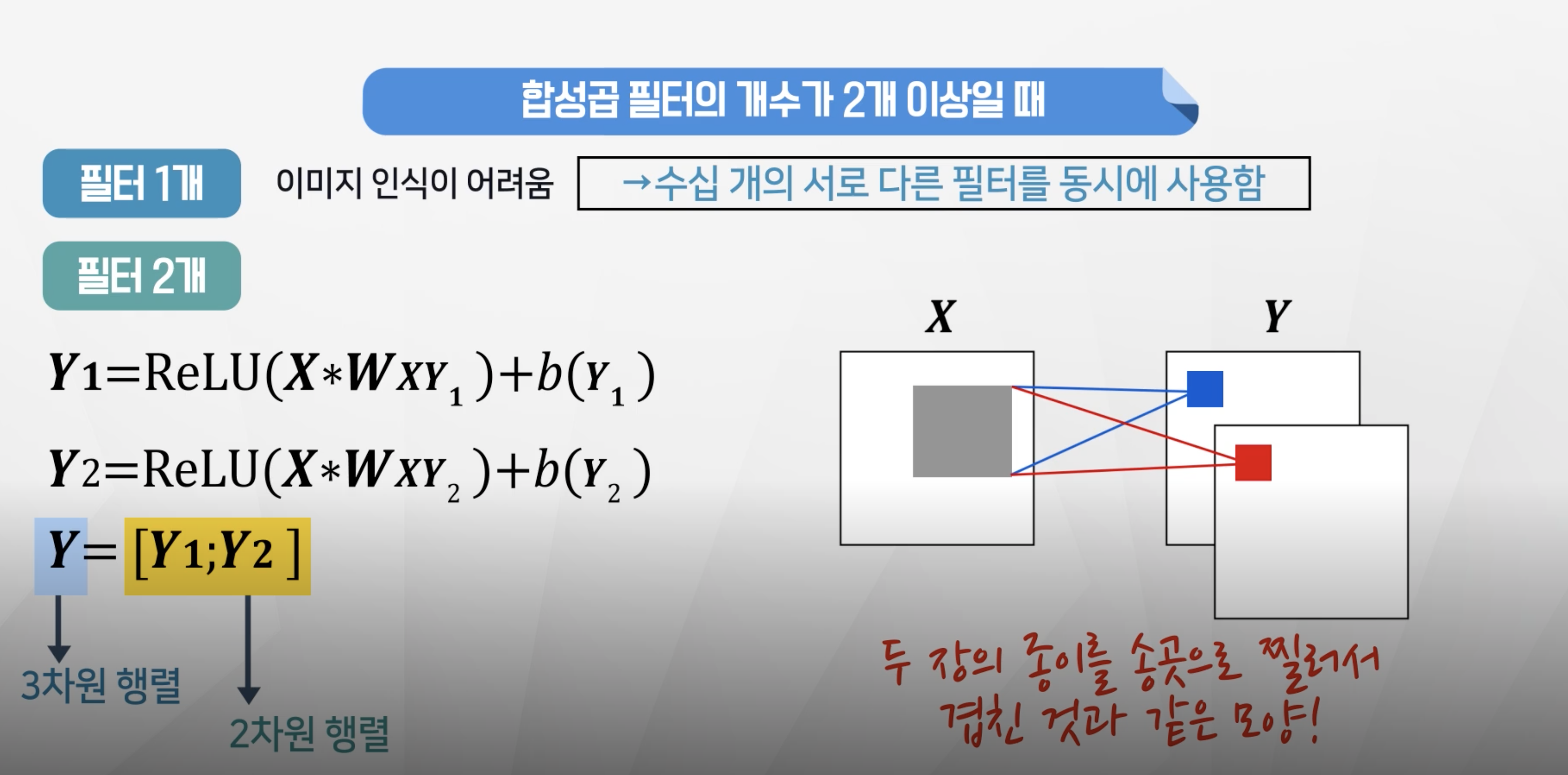
• 필터가 1개만 존재할 경우 이미지 인식에 한계가 있음
• 수십 개의 서로 다른 필터를 동시에 사용한다.
• 필터1을 통과한 y1과 필터2를 통과한 y2가 결과로 나와서 3차원 행렬이 되게된다.
  
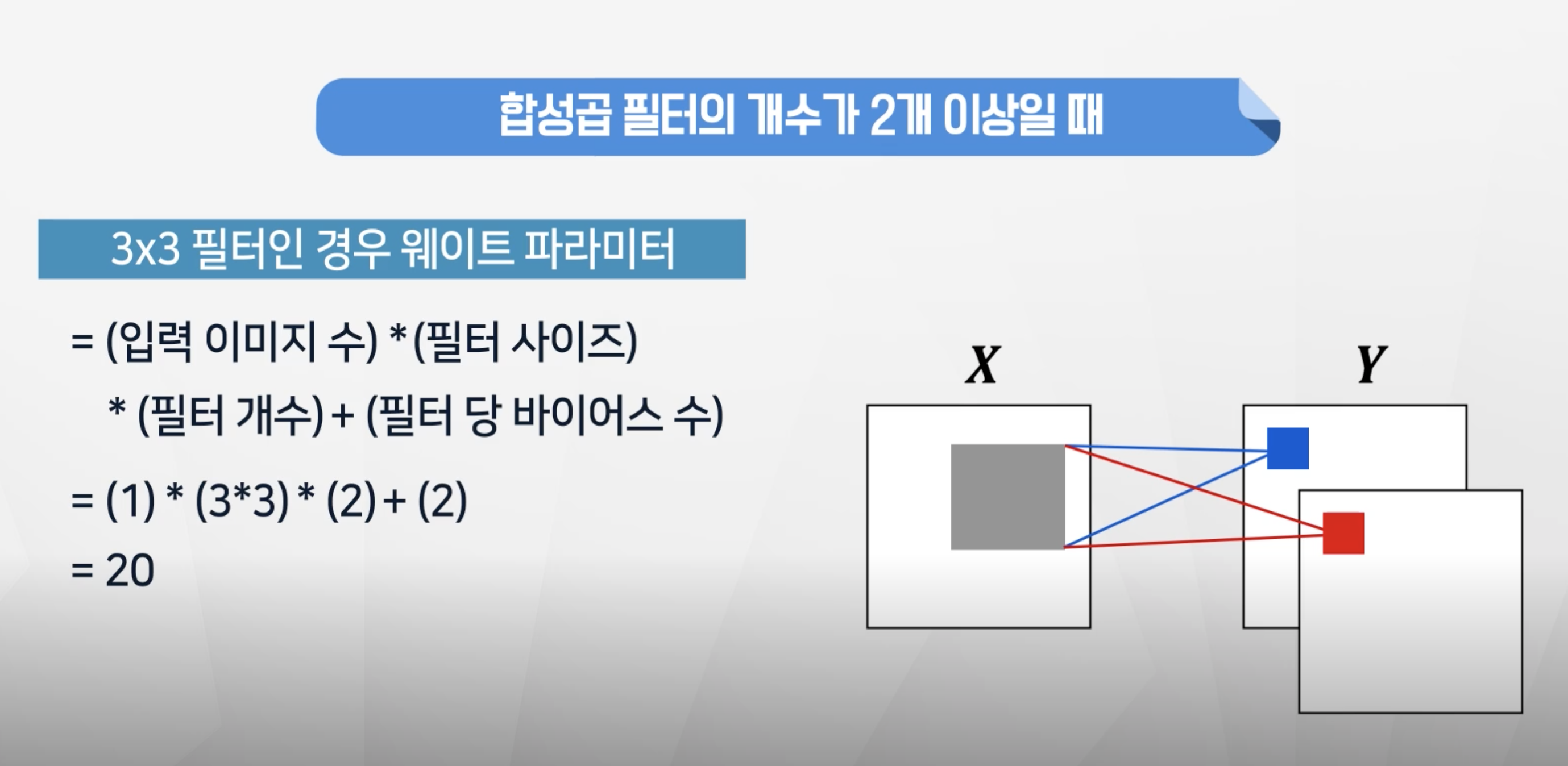
• 학습할 파라미터는 이미지 1개 입력시 1 x 3x3 x2 +2 = 20개

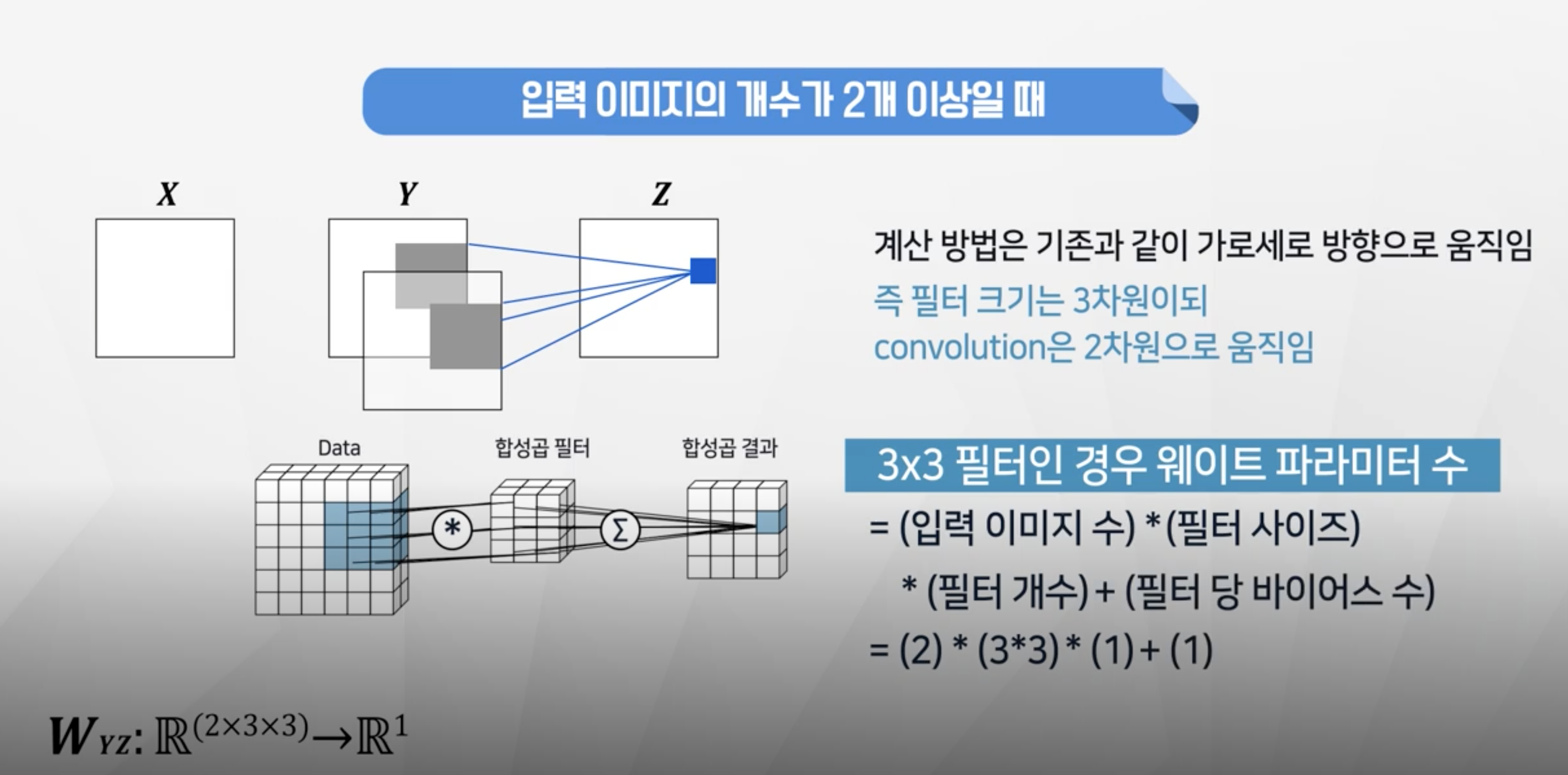
• 입력이미지가 2개일 때는 깊이 부분이 한 덩어리로 움직이게 된다.
• 학습할 파라미터는 이미지 2개 입력시 2 x 3x3 x1 +1 = 19개

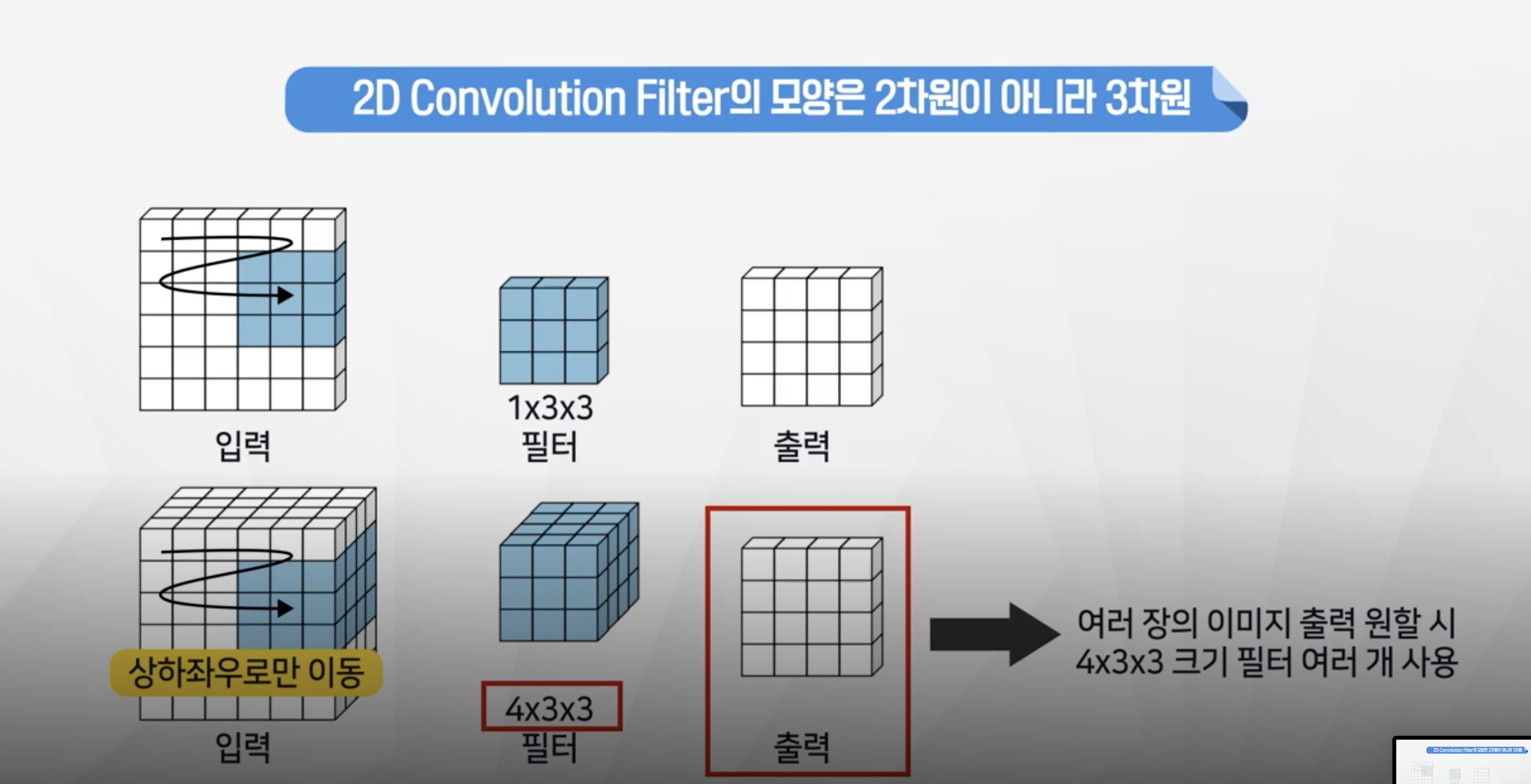
• 필터가 깊이를 동시에 움직이기 때문에 결과는 2차원으로 출력이 됌.

Simple CNN Structure

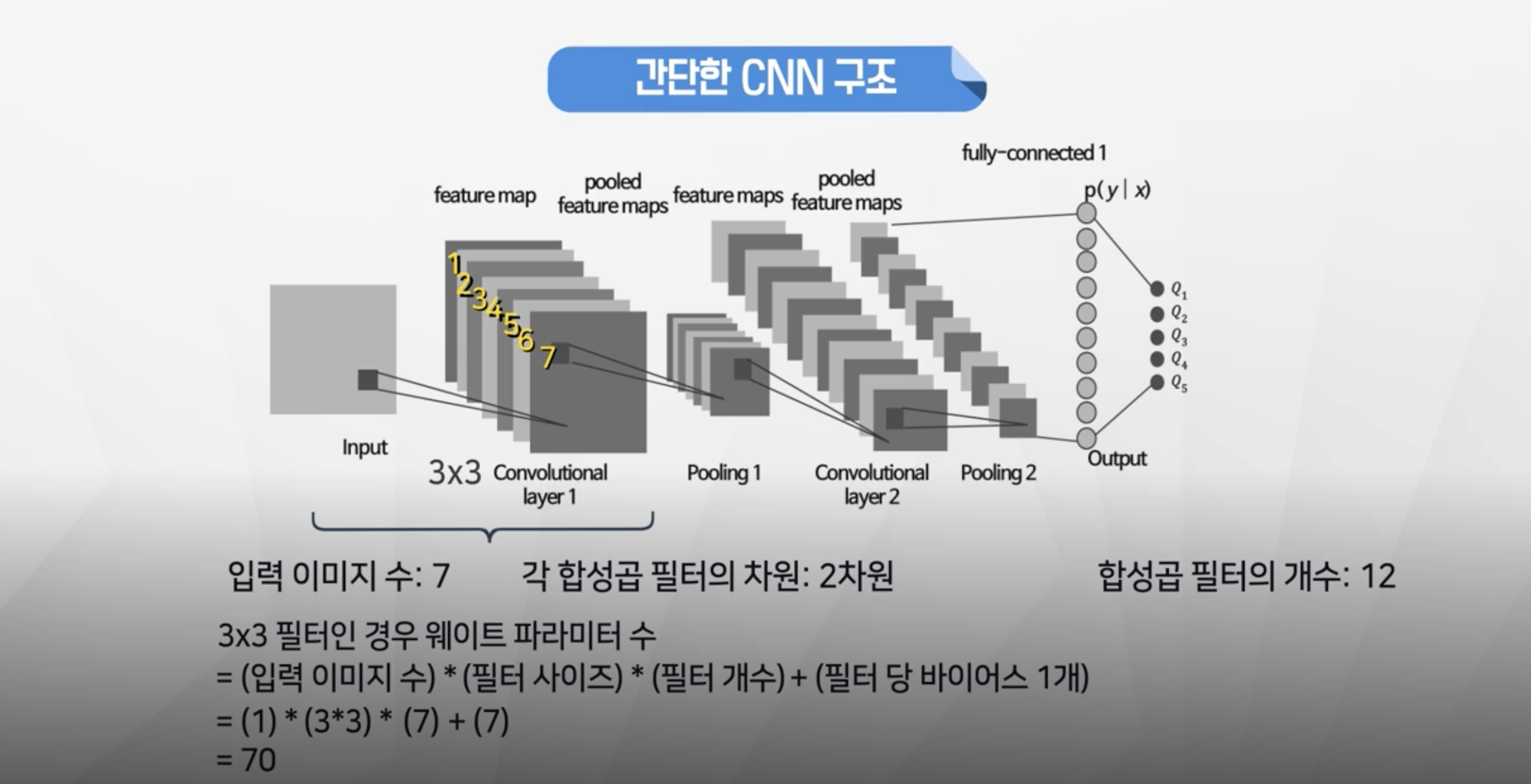
• 우선 1차 CNN을 진행
• 입력이미지 : 1개
• 필터 형태: 3*3
• 필터 개수 : 7개
• 최종 파라미터 개수 : 1 x 3x3 x 7 +7 = 70

Pooling Layer

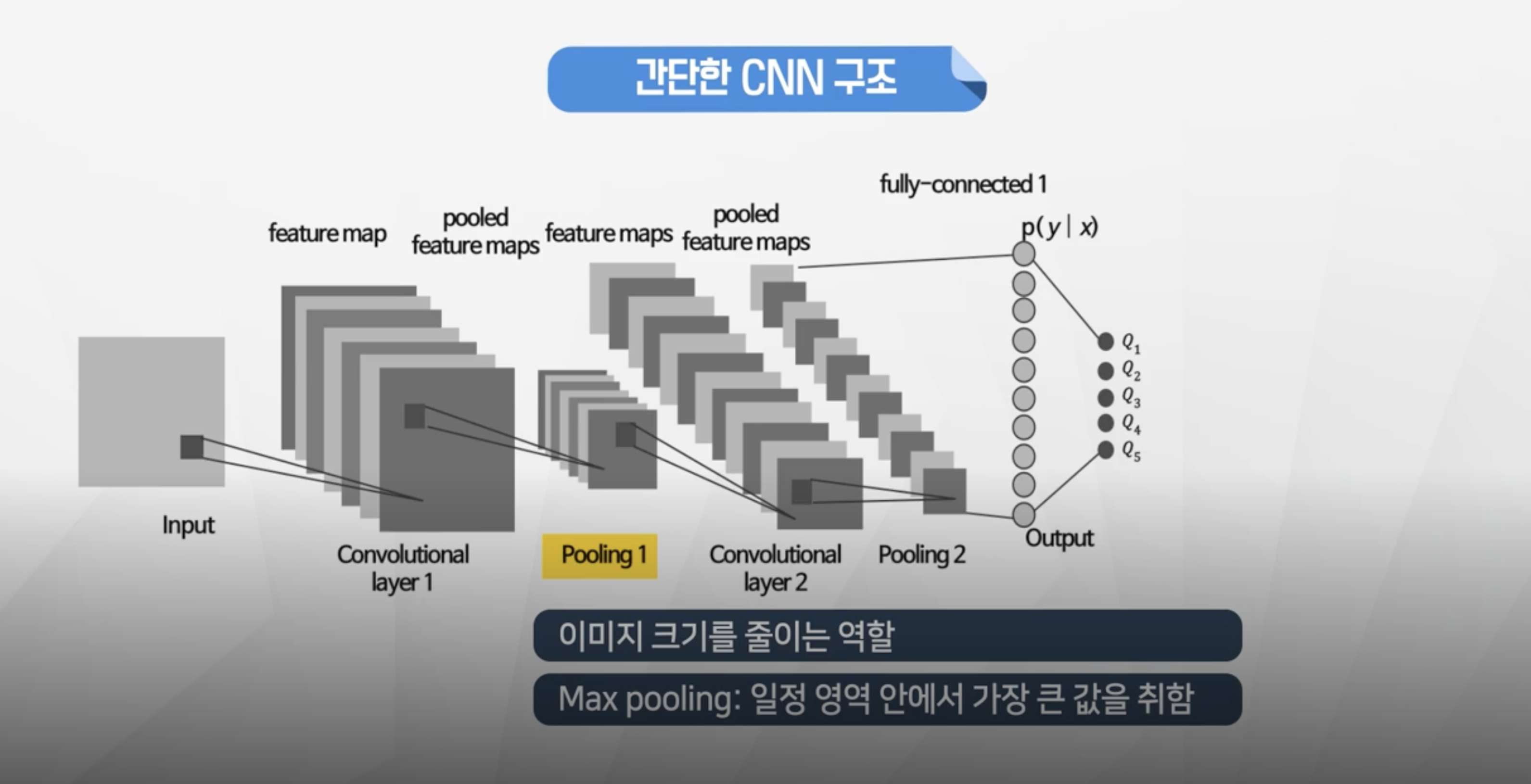
• 이미지 크기를 줄이는 역할!
• max pooling이 효과가 좋음

• 4X4행렬에서 2x2 행렬안에 존재하는 값들중 가장 큰 값만 가져온다.

• 그러면 4X4행렬에서 2x2행렬로 크기가 줄어든다.

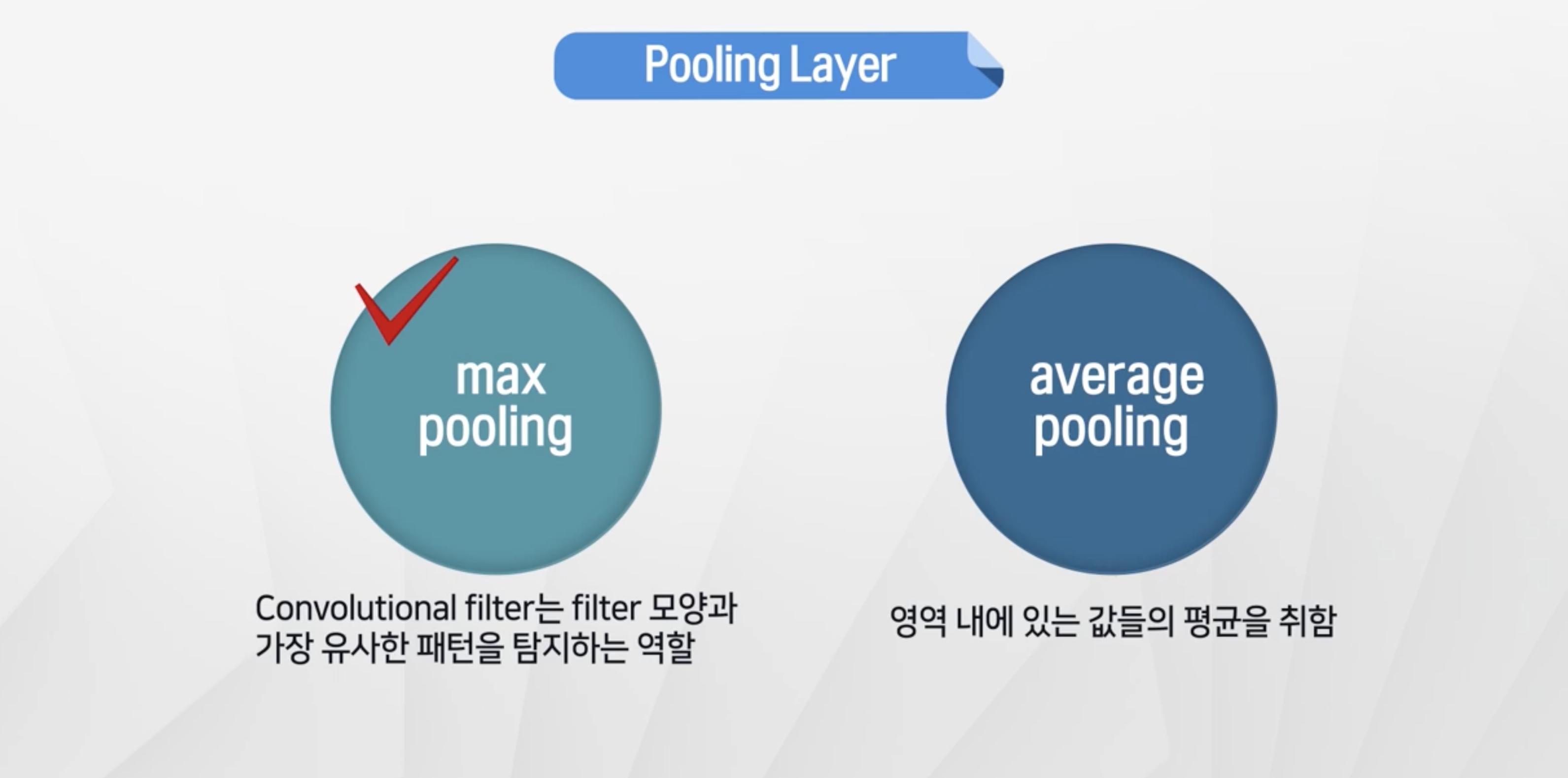
• 두가지 방법이 존재
• max pooling - 합성곱의 max값 → 패턴과 일치하는 정도가 높은 것을 채택
• average pooling : 평균으로 계산 → 패턴과 일치하는 정도가 약해짐

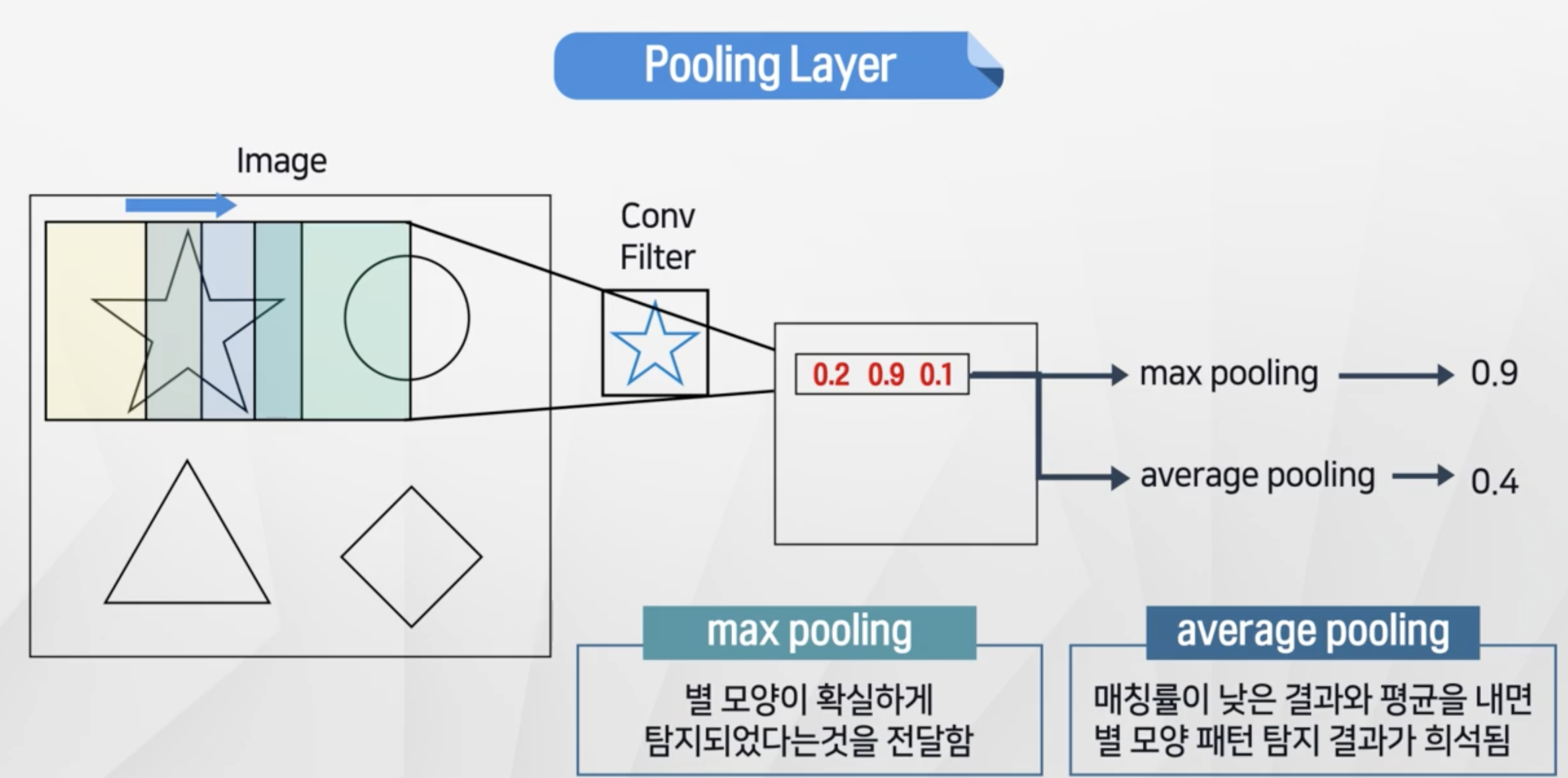
• 조금 더 별모양과 패턴이 일치하는 형태가 두드러진다.

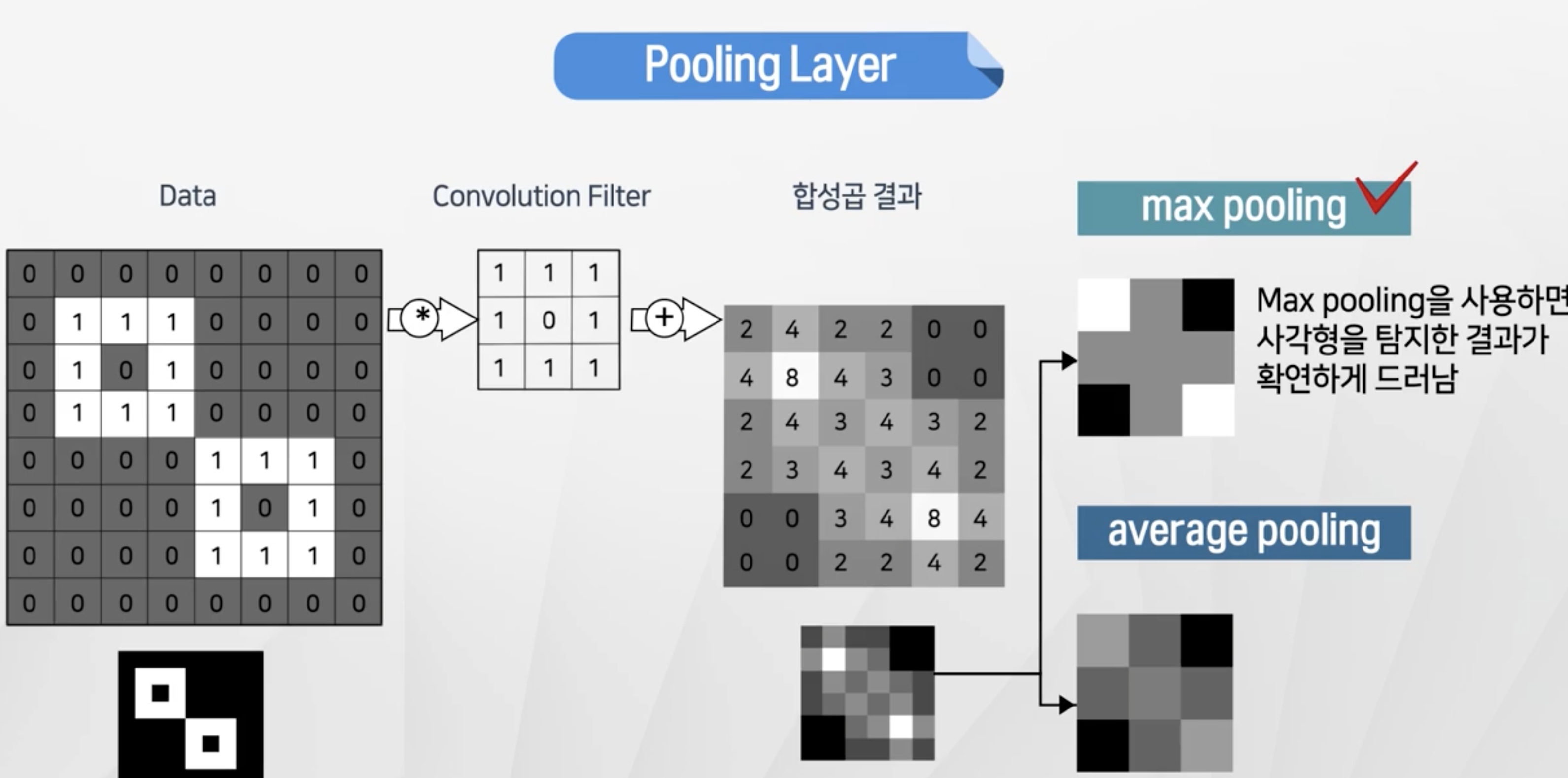
Second Convolution Layer

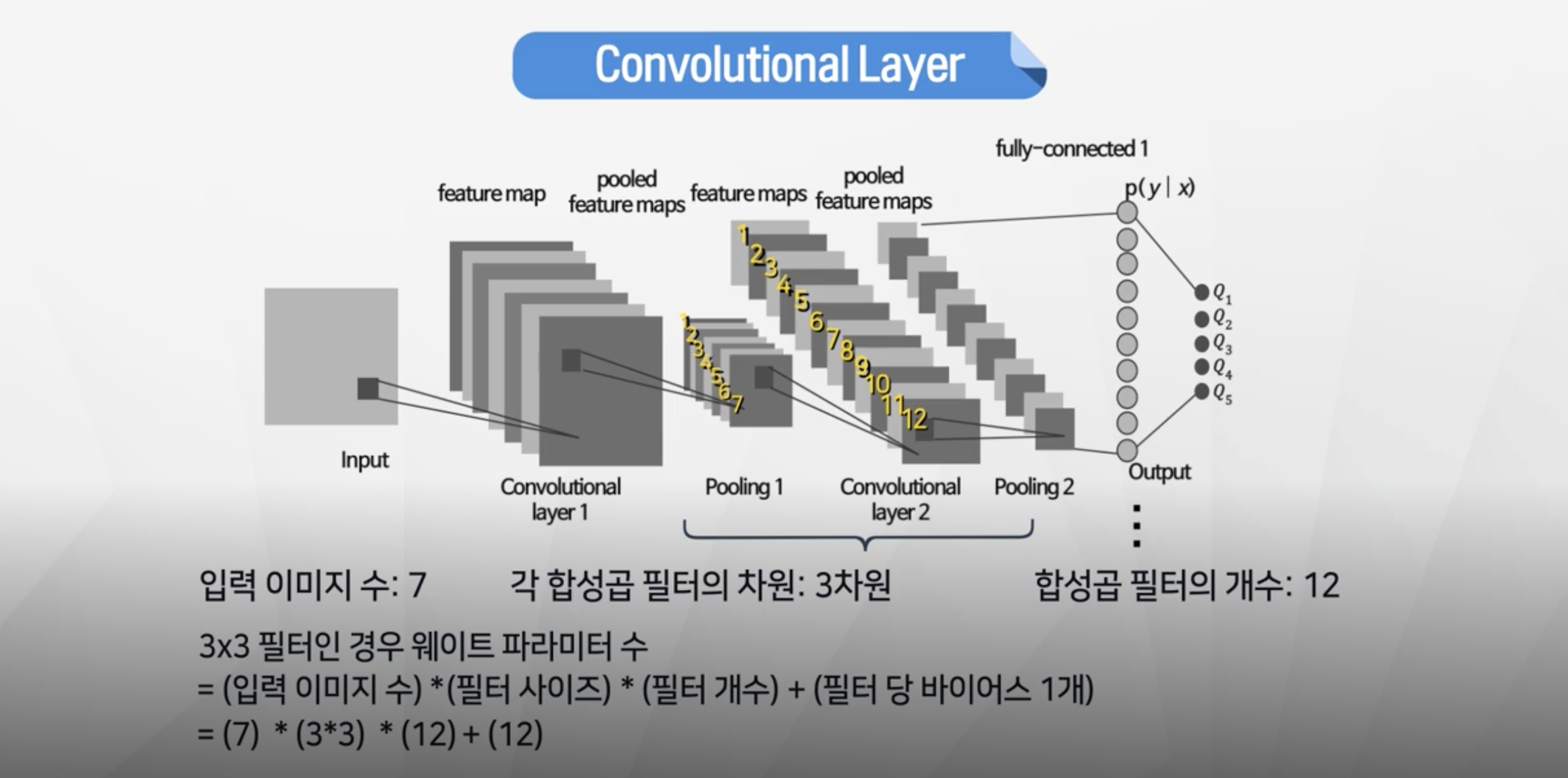
• 이미지 수 : 7개 (1개이미지에 7개 필터 적용 + 풀링된 결과)
• 필터 형태 : 3x3
• 필터 개수 : 12개
• 파라미터 개수 : 7 x 3x3 x 12 +12 = 768개

Falttening

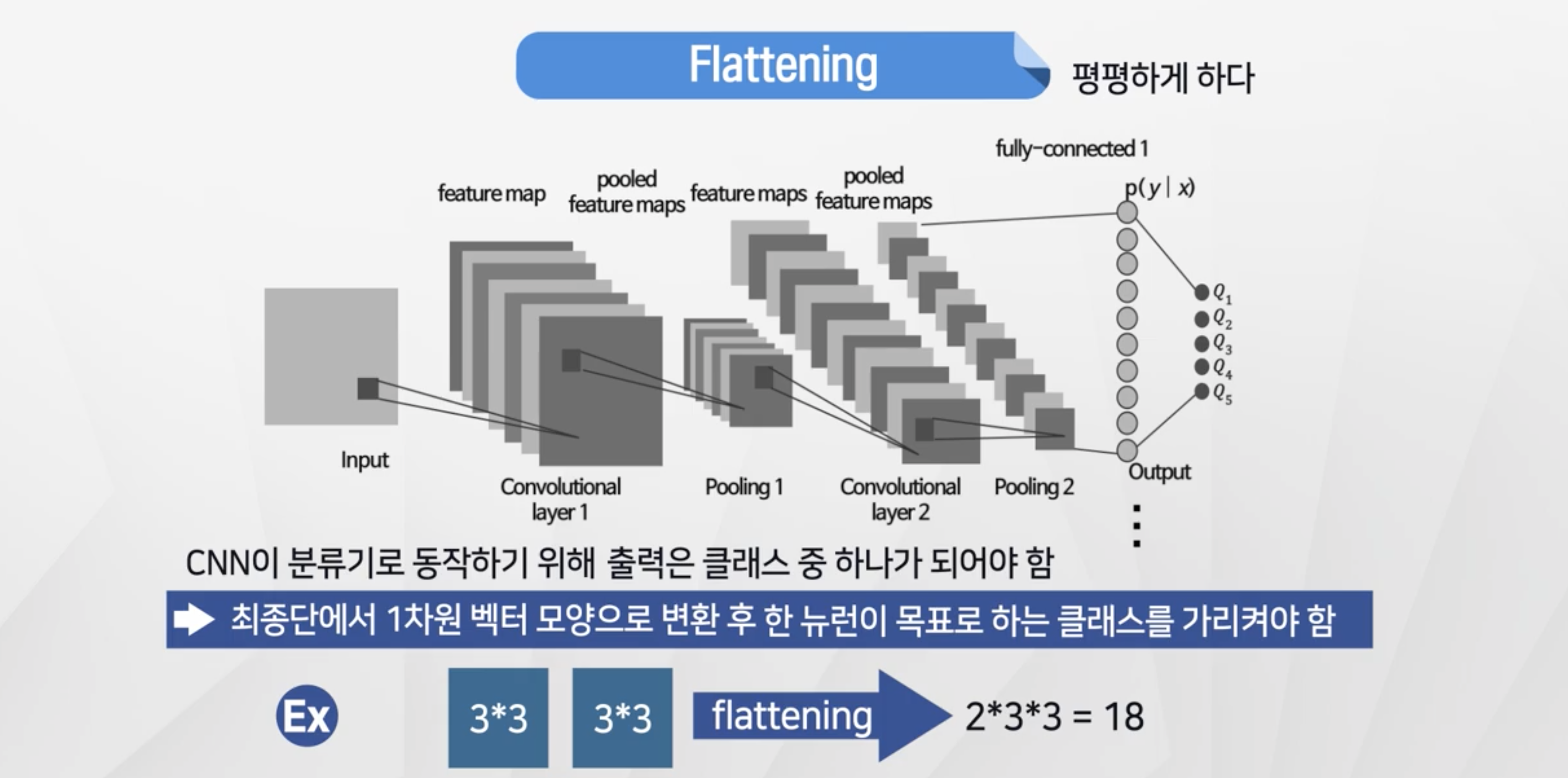
• 현재 상태 : 숫자행렬로 표시된 이미지 형태
• 이미지를 각 클래스로 분류를 하려면 1차원 벡터로 변환 필요
• 3x3, 3x3 → 2x3x3 = 18로 치환

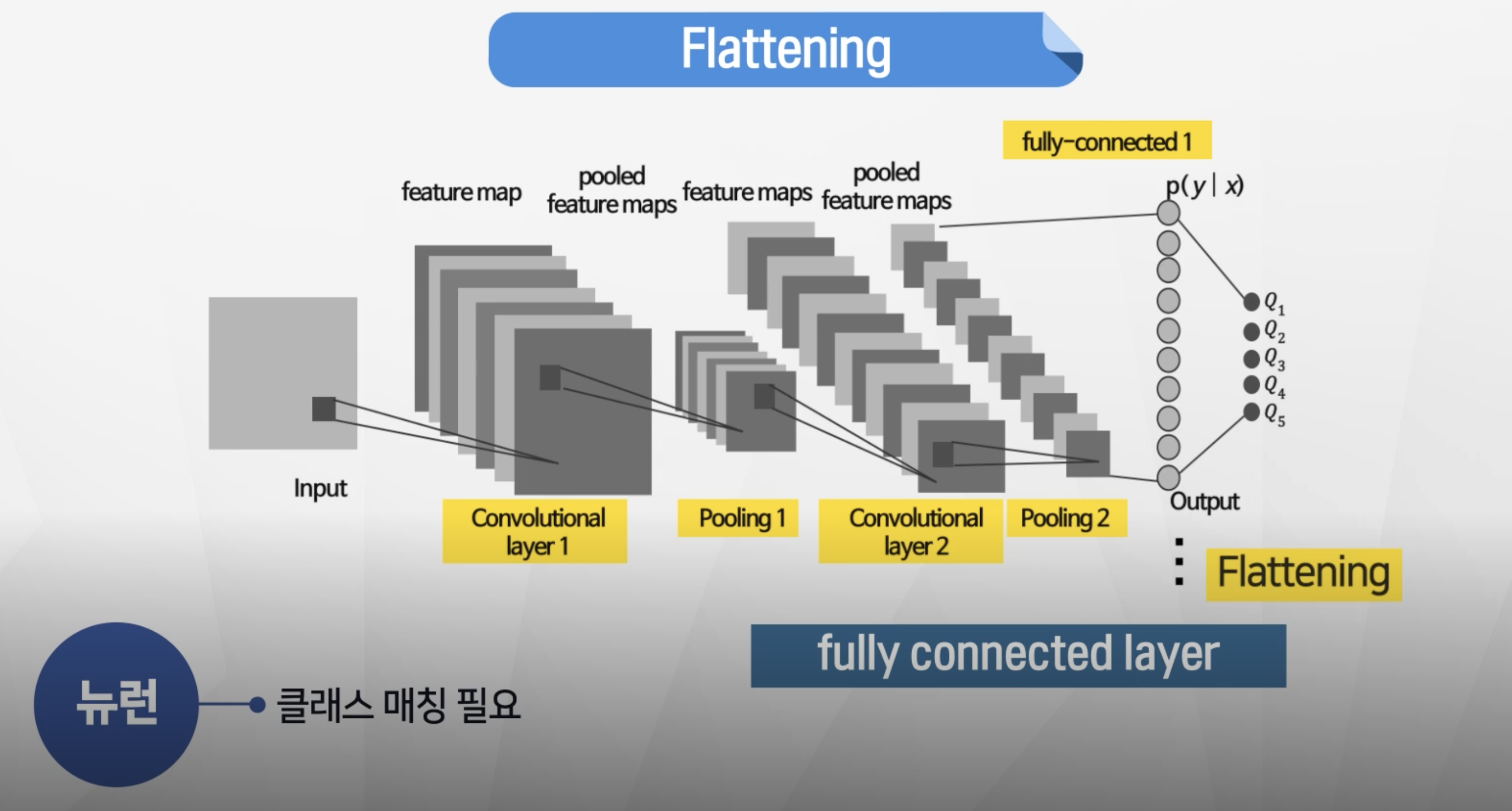
• 치환된 값을 fully-connected-layer에서 출력 반환
• fully-connected-layer가 2개 이상 있을 수 있음.(필요한 만큼)
• 출력 뉴런개수 = 인식하고자 하는 클래스 수!

Softmax

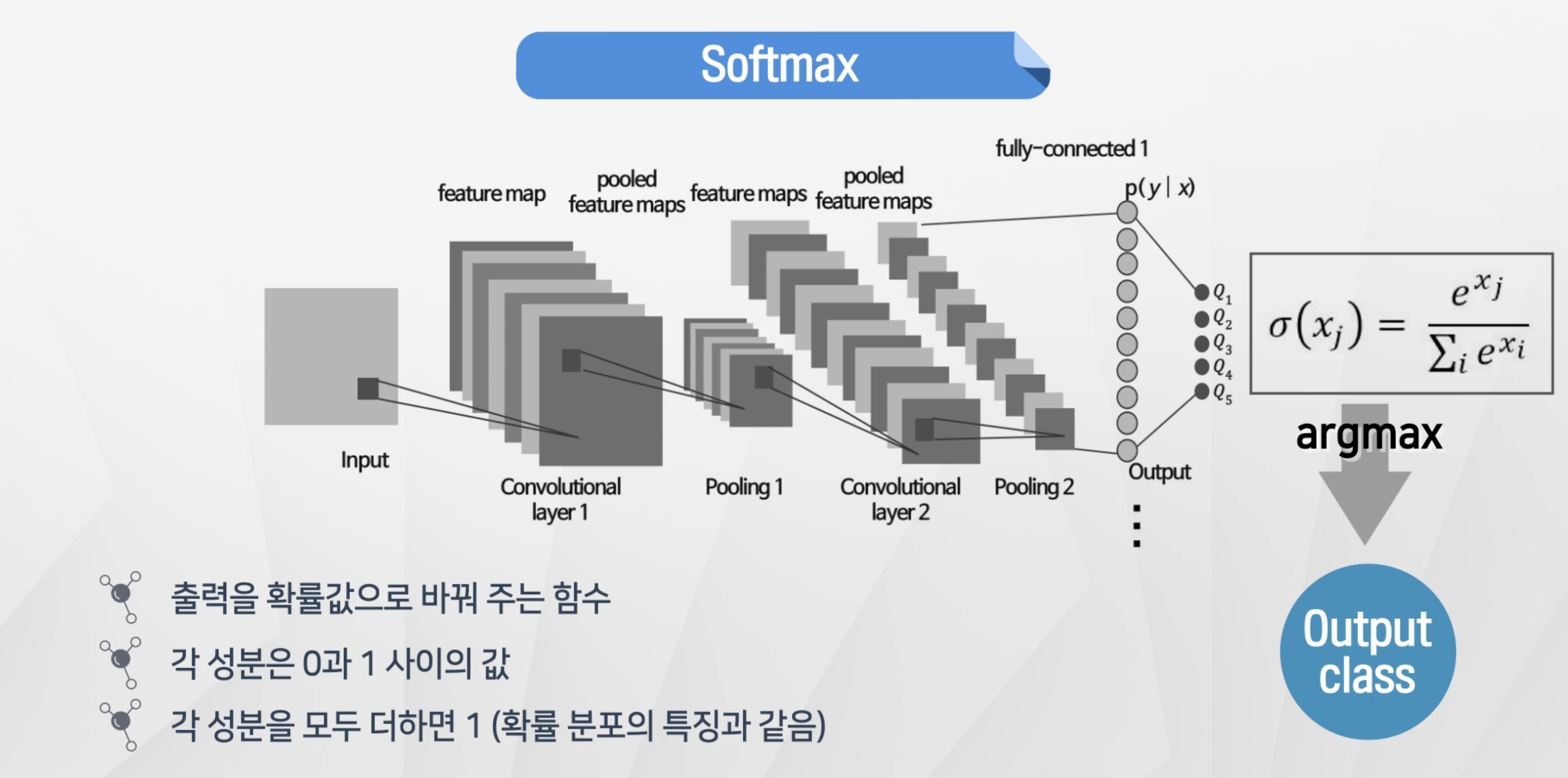
• 출력을 확률값으로 바꿔 주는 함수
• 각 성분은 0~1사이
• 각 성분을 모두 더하면 1
• 나온 결과를 argmax에 적용을 해서 최종 output-class를 판단

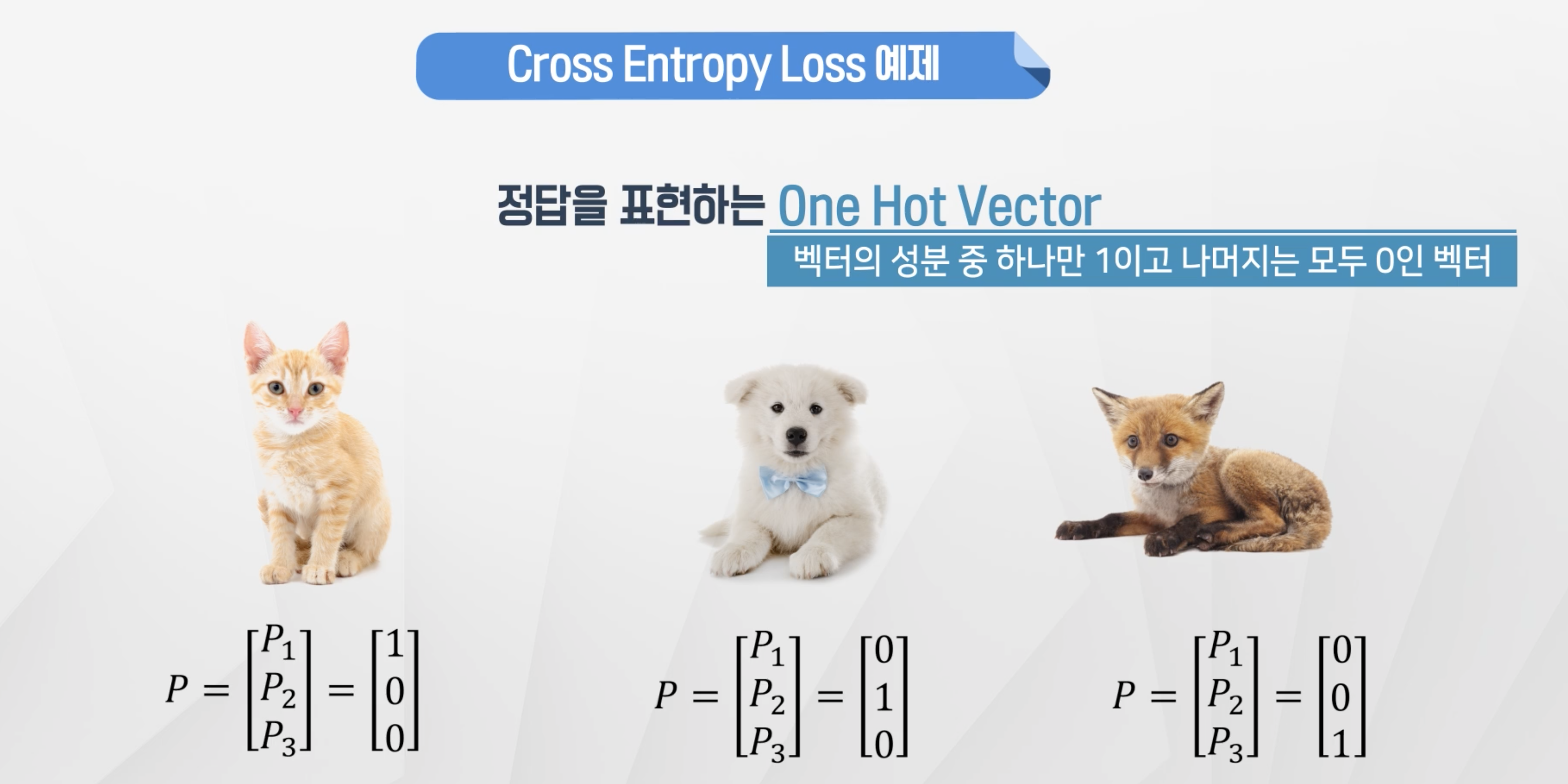
Cross Entrophy & Loss

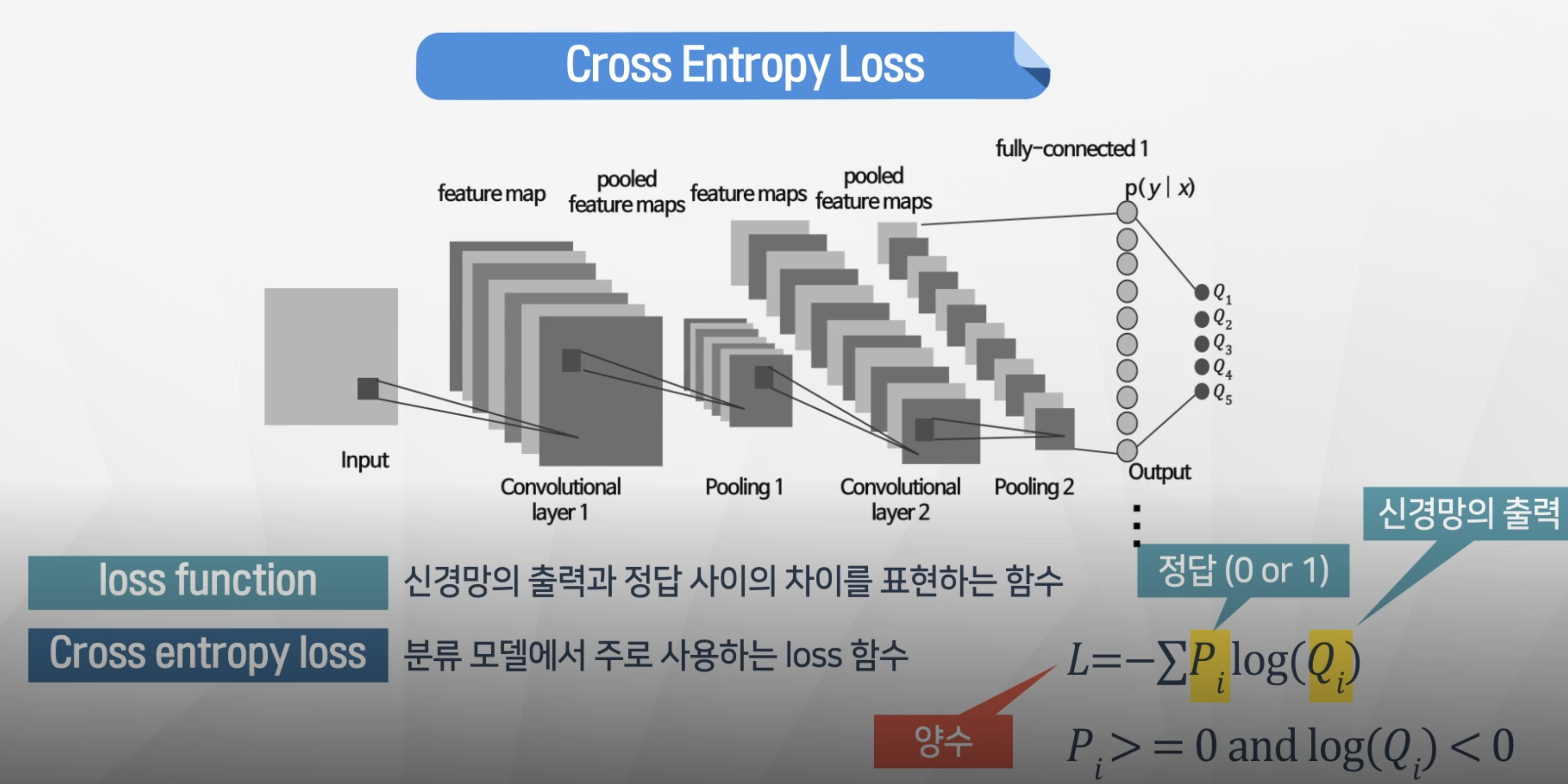
• 분류문제에 경우 cross-entrophy로 성능을 측정
• 정답 (0 or 1)
• log(softmax 출력값) 항상 음수 // 0< softmax출력값 <1
• L = 양수

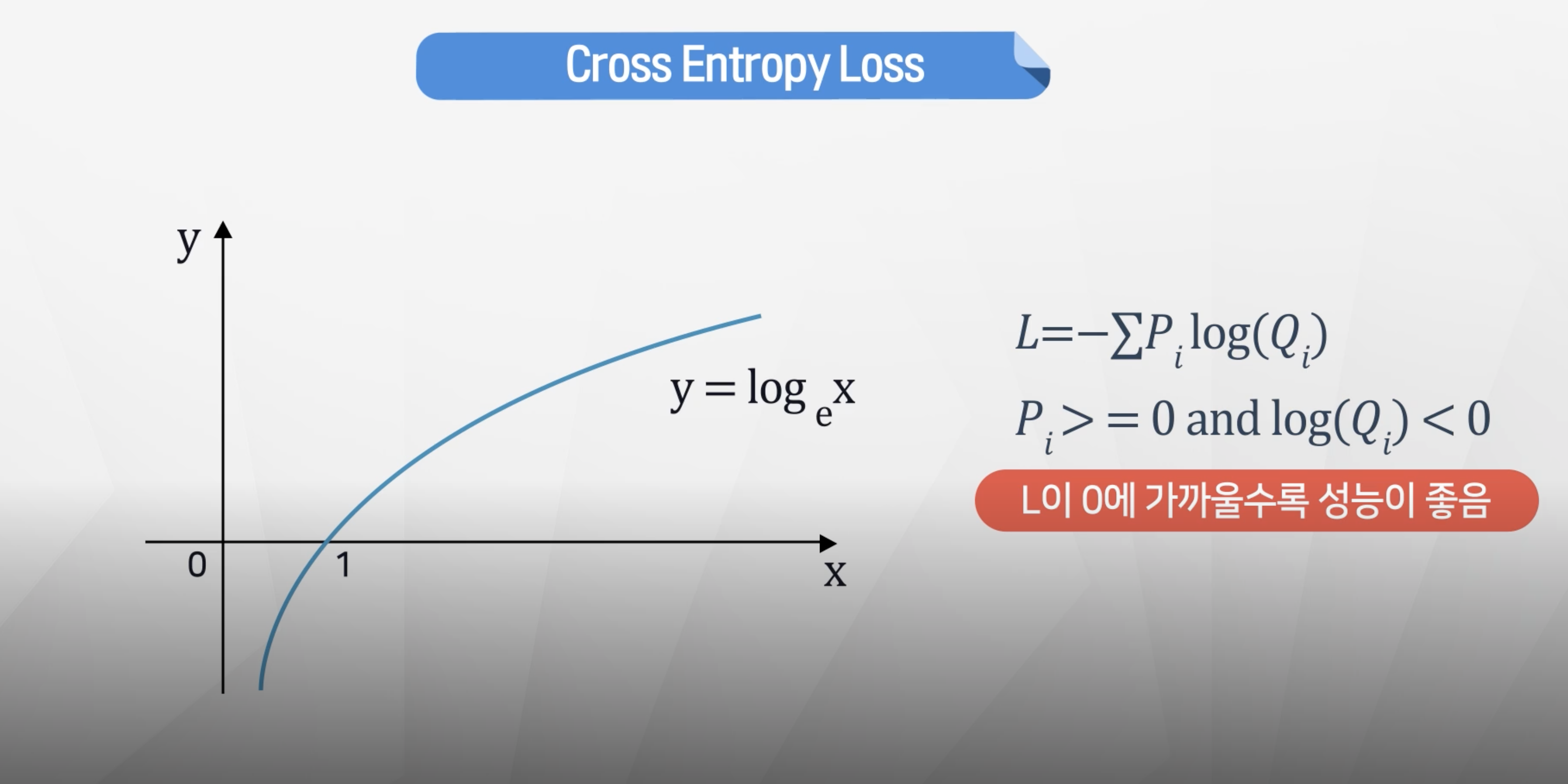
• 만일 대상이 1을 가정했을 때 Q의 값이 1에 가깝다면 log(Q)는 0에 가까워지고 그에 따라 loss도 작아지게 된다.

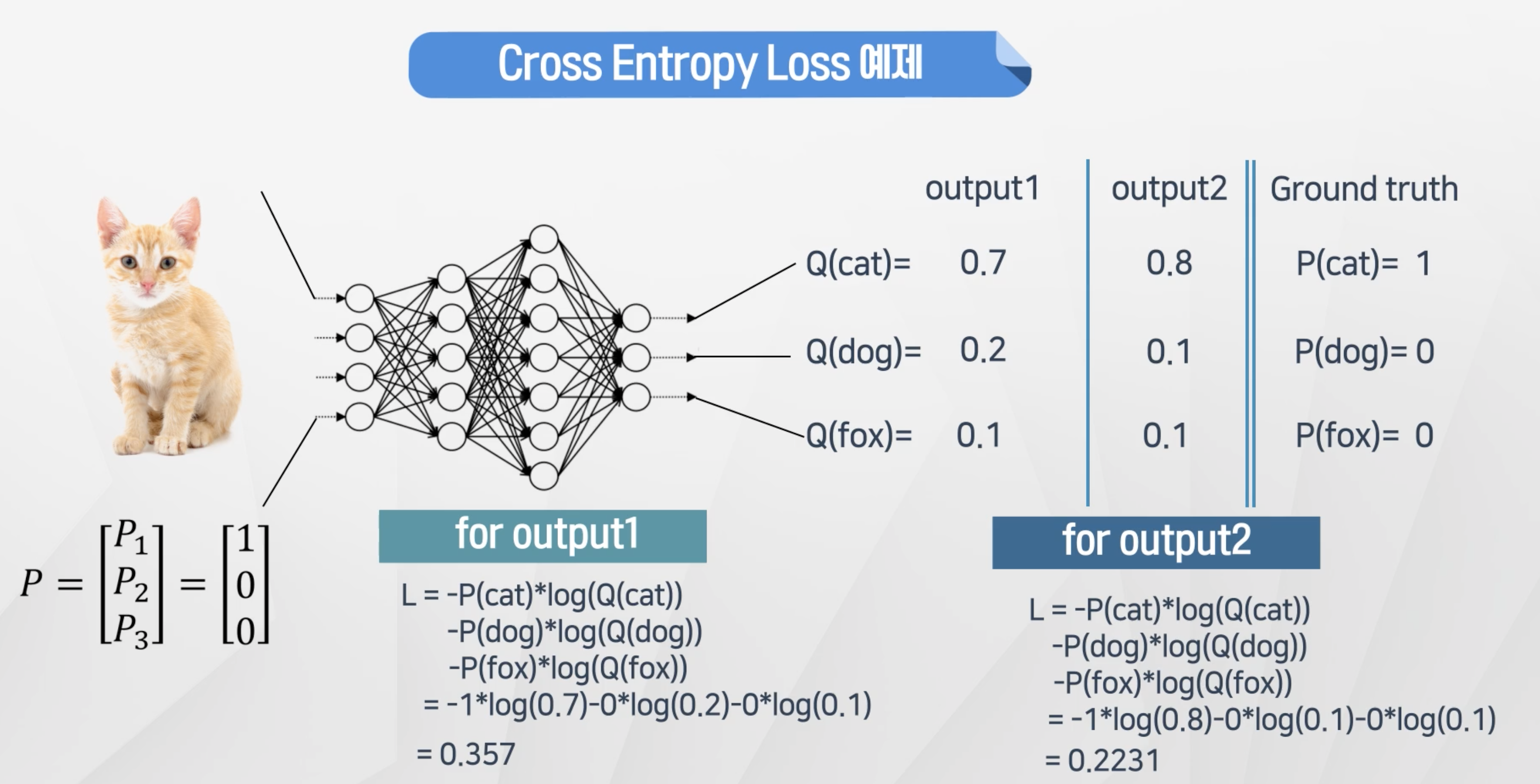
• Output2의 Cross-Entrophy가 낮다 → Output2가 결과를 더 예측 잘 했다는 것을 알 수 있다.

결론

• weight는 backpropagation을 통해서 optimizer가 자동으로 수행을 한다.

• 그러면 성능을 향상시키기 위해서는 레이어 개수, 필터 사이즈, 필터 개수, 풀링 사이즈 등을 최적화하며 모델을 찾아야 한다.