01. 기본 배경 개념

📌 그래프(GRAPH)

• 그래프(graph)의 개념

  • 정점(node)과 간선(edge)으로 이루어진 자료구조의 일종. G = (V, E)

• 그래프 탐색

  • 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것
    ex) 특정 도시에서 다른 도시로 갈 수 있는지 없는지, 전자 회로에서 특정 단자와 단자가 서로 연결되어 있는지

02. DFS

📌 DFS(Depth First Search)의 개념

• 깊이 우선 탐색 방법으로 시작점(루트 노드(혹은 다른 임의의 노드))에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법으로 루트 노드와 같은 거리에 있는 노드를 우선전으로 탐색하는 개념이다.

  ex) 미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가
  	 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서
  	 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사함

📌 DFS의 특징

• 즉 넓게(wide) 탐색하기 전에 깊게(deep) 탐색함
• 모든 노드를 방문하고자 하는 경우에 이 방법을 선택함
• 깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단함
• 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느림

📌 DFS의 장단점

• 장점

  • 현 경로상의 노드들만 기억하면 되므로 저장공간 수요가 비교적 적다.
  • 목표 노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있다.

• 단점

  • 해가 없는 경로가 깊을 경우 탐색시간이 오래 걸릴 수 있다.
  • 얻어진 해가 최단 경로가 된다는 보장이 없다.
  • 깊이가 무한히 깊어지면 스택오버플로우가 발생할 위험이 있다.(깊이 제한을 두는 방법으로 해결가능)

📌 알고리즘 구현

• 스택 활용 시

  1. 스택을 하나 만든다. 빈 스택에 시작할 노드를 넣는다.
  2. 스택에서 노드를 하나 꺼내고(pop), 출력한다.
     그리고 꺼낸 노드로 부터 분기된 노드들을 다 넣는다.
     이때 한 번 스택에 담은 노드는 다시 넣지 않음
  3. 반복한다.

• 재귀 활용시

  1. 노드의 분기를 계속 호출하고 들어간 다음
  2. 더이상 분기가 없으면(마지막 노드라면)
     하나 올라와서 올라온 지점의 다른 경로로부터 탐색을 다시 시작한다.

📌 알고리즘 구현시 유의점

• 자기 자신을 호출하는 순환 알고리즘의 형태를 지님
• 이 알고리즘을 구현할 때 가장 큰 차이점은 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야한다는 것 (이를 검사하지 않을 경우 무한루프에 빠질 위험이 있음)

03. BFS

📌 BFS(Breadth First Search)의 개념

• 너비 우선 탐색 방법으로, 시작점인 루트 노드와 같은 거리에 있는 노드를 우선으로 탐색하는 방법으로,
  시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 탐색한다.

  ex) 지구 상에 존재하는 모든 친구 관계를 그래프로 표현한 후
  	 Ash 와 Vanessa 사이에 존재하는 경로를 찾는 경우

• 깊이 우선 탐색의 경우 - 모든 친구 관계를 다 살펴봐야 할지도 모름
• 너비 우선 탐색의 경우 - Ash과 가까운 관계부터 탐색

📌 BFS의 특징

• 즉 깊게(deep) 탐색하기 전에 넓게(wide) 탐색함
• 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 이 방법을 선택함

📌 BFS의 장단점

• 장점

  • 너비를 우선으로 탐색하므로 답이 되는 경로가 여러 개인 경우에도 최단경로를 얻을 수 있다.
  • 경로가 무한히 깊어져도 최단경로를 반드시 찾을 수 잇다.
  • 노드 수가 적고 깊이가 얕은 해가 존재할 때 유리하다.

• 단점

  • DFS와 달리 큐를 이용하여 다음에 탐색할 정점들을 저장하므로 더 큰 저장공간이 필요하다.

📌 알고리즘 구현

• 큐 활용 시

  1. 빈 큐를 만들고 시작 노드를 넣는다.
  2. 큐에서 노드를 꺼내고(pop), 출력한다.
     꺼낸 노드의 분기들을 큐에 추가한다
     이때 한 번 큐에 담은 노드는 다시 넣지 않음)
  3. 반복한다.

📌 알고리즘 구현시 유의점

• BFS 는 재귀적으로 동작하지 않는다.

• 이 알고리즘을 구현할 때 가장 큰 차이점은 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야한다는 것이다 이를 검사하지 않을 경우 무한 루프에 빠질 위험이 있다.

• BFS 는 방문한 노드들을 차례로 저장한 후 꺼낼 수 있는 자료 구조인 큐(Queue)를 사용함

• 즉 선입선출(FIFO) 원칙으로 탐색

04. 차이점

📌 탐색 순서

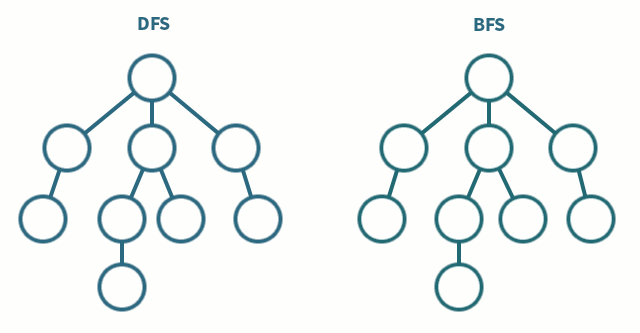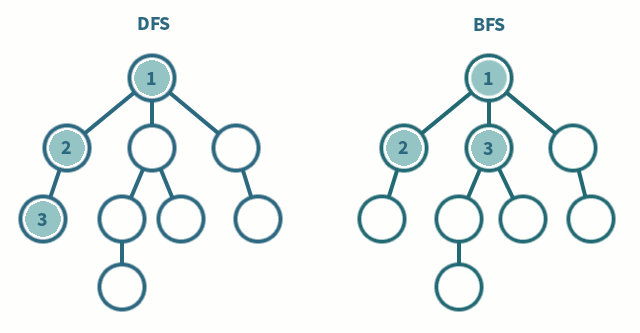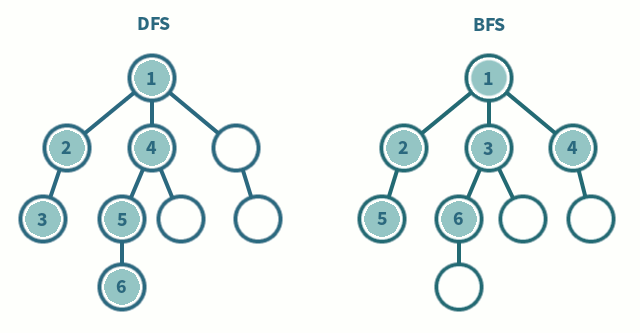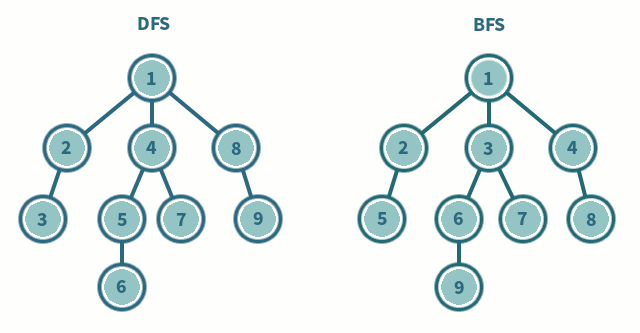
📌 특징

	DFS(깊이우선탐색)	BFS(너비우선탐색)
범위	현재 노드에서 끝까지 분기하여 탐색	현재 노드에서 인접한 노드(1번 분기)들 우선 탐색
시간복잡도(인접행렬)	O(n^2)	O(n^2)
시간복잡도(인접리스트)	O(n+e)	O(n+e)
구현	스택 or 재귀	큐&덱
적합한 문제 유형	경로의 특징 확인 문제, 탐색 범위가 클 때	최단거리 문제, 탐색 범위가 작을 때

- 참고 링크

https://yunyoung1819.tistory.com/86
https://devyuseon.github.io/algorithm/dfs-and-bfs/
https://currygamedev.tistory.com/10
https://velog.io/@lucky-korma/DFS-BFS%EC%9D%98-%EC%84%A4%EB%AA%85-%EC%B0%A8%EC%9D%B4%EC%A0%90
https://cyc1am3n.github.io/2019/04/26/bfs_dfs_with_python.html