00. 고민의 배경?
-
코딩 연습문제를 풀다보면 파이참 환경에서는 출력이 가능하나,
제출 시 시간초과로 인해 오답처리되는 경우가 빈번하다. -
같은 결과를 반환하는 코드도 구성에 따라서 걸리는 시간이 다르게 나타난다.
-
코드에 따른 출력 시간이 어떻게 걸리는지 알아보자.
-
아래 내용은 다음의 블로그 내용을 주로 참고하였다.
출처 : 코딩 팩토리 티스토리
출처 : 인생의 로그캣 티스토리
01. 시간복잡도
특정 알고리즘이 결과를 반환하는데(문제를 푸는데) 걸리는 시간
- 같은 결과를 반환하는 소스라면 최대한 시간이 적게 걸리는 것이 좋은 소스이다. 그렇기에 더 효율적인 알고리즘을 구성하기 위해서 시간 복잡도의 측면을 고려해야한다.
02. 빅-오 표기법(Big - O notation)
빅오 표기법은 알고리즘의 효율성을 표기해주는 시간 복잡도 표기법이다.
-
알고리즘의 효율성은 데이터 개수(n)가 주어졌을 때 덧셈, 뺄셈, 곱셈 같은 기본 연산의 횟수를 의미한다.
-
시간 복잡도에는 여러 개념이 있지만 그중에서 ‘아무리 많이 걸려도 이 시간 안에는 끝날 것‘의 개념이 제일 중요하다.
-
예를 들어 동전을 튕겨서 뒷면이 나올 확률을 이야기해본다면 운이 좋으면 한 번에 뒷면이 나올 수도 있고 운이 좋지 않으면 3번 4번만에 뒷면이 나올수도 있다.
-
이 최악의 경우를 계산하는 방식을 빅-오(Big-O) 표기법이라고 부르며 이 방식을 가장 많이 사용합니다.
03. 빅-오 표기법의 종류 및 처리시간
- 표기법 종류에 따른 구분
| 표기법 | 영문명 | 수식 | 데이터8배 시 처리시간 | 예시 |
|---|---|---|---|---|
| O(1) | Constant | 상수함수 | 1배(변함없음) | push, pop, remove 등 |
| O(log₂n) | Logarithmic | 로그함수 | 3배 | 이진탐색, 순기능 재귀 |
| O(n) | Linear | 선형함수 | 8배 | for 문 |
| O(n log₂n)* | Linear-Logarithmic | 선형로그함수 | 24배 | 퀵 정렬(quick sort), 병합정렬(merge sort), 힙 정렬(heap Sort) |
| O(n²) | quadratic | 다항함수 | 64배 | 이중 for 문, 삽입정렬(insertion sort), 거품정렬(bubble sort), 선택정렬(selection sort) |
| O(2ⁿ) | Exponential | 지수함수 | 256배 | 피보나치 수열, 역기능 재귀 |
-
입력한 데이터 개수에 따른 알고리즘 효율성
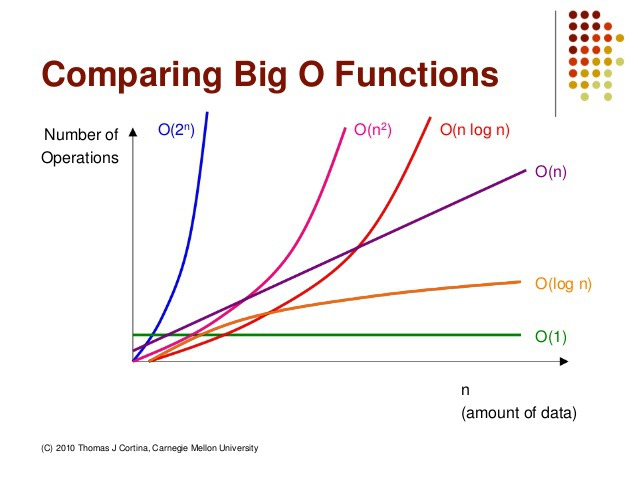
-
시간복잡도(우측으로 갈수록 효율성 하락)
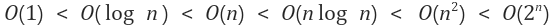
-
실행시간 예측(우측으로 갈수록 데이터양 2배씩 상승)
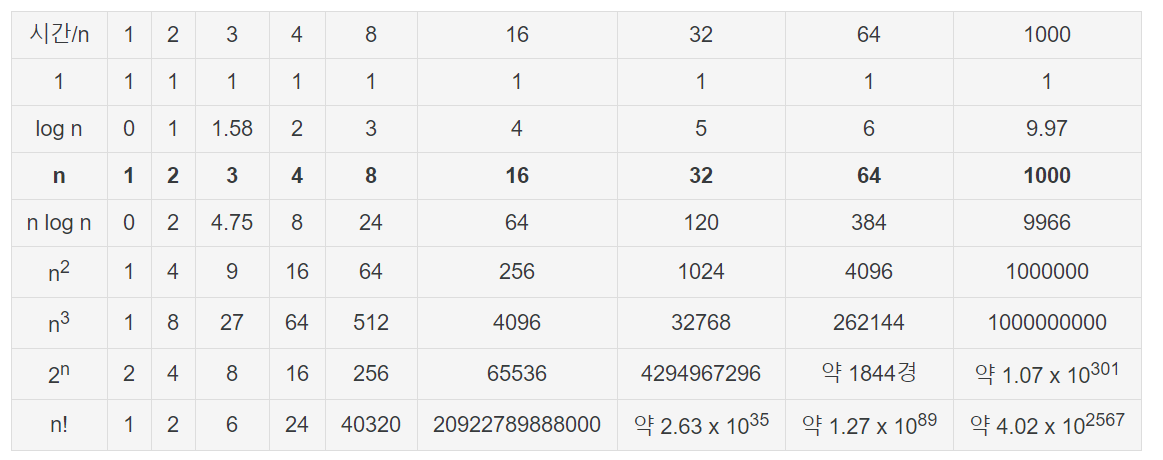
- 파이썬은 1초에 2천만 번의 연산 가능
- 만약 1만번의 입력데이터가 들어온다면?
① O(n) : 0.1초
② O(n²) : 1초(1만 * 1만 = 1억)
_ - 조건부 문제 해결 시(데이터 : 1억 개 / 실행시간 : 1초)
: O(n)이나 O(Log N)의 시간 복잡도로 문제를 풀어야 함
04. 빅-오 표기법 특징
영향력 없는 항 무시
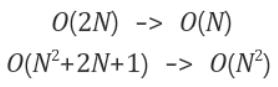
- 위와 같이 가장 크게 영향을 끼치는 최고차항을 제외한 다른 항이나 계수는 무시하고 표기한다
05. 시간 복잡도 줄이기
1) 반복문 없애기
- 반복문을 중첩시킬 경우 시간복잡도가 한 차원 증가
2) 효율적인 자료구조 사용
- 자료 구조에 따른 시간복잡도 표를 활용하여 사용
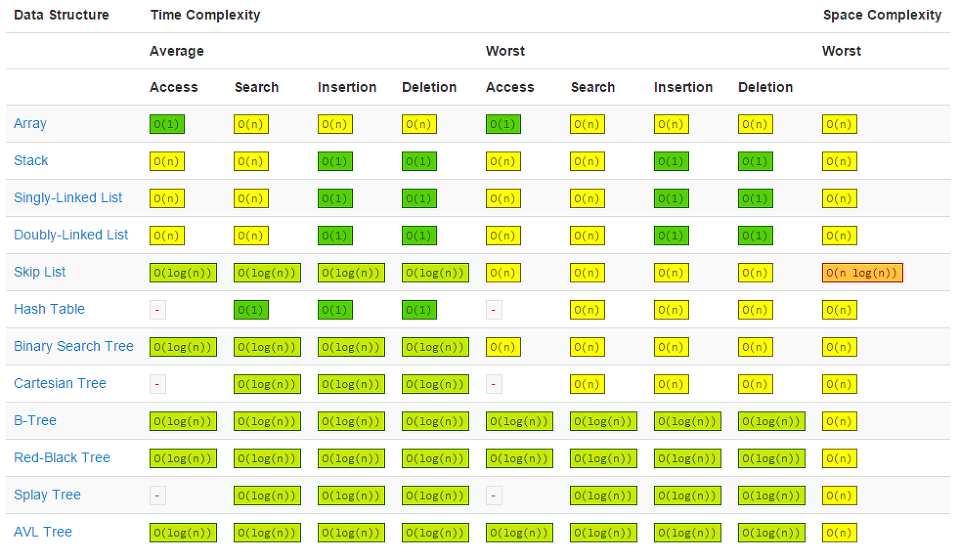
3) 적절한 알고리즘 사용
- 알고리즘에 따른 시간복잡도 표를 활용하여 사용