[99클럽] 백준 2212 센서

문제 링크

문제

• N개의 센서를 도로 위에 설치하고, K개의 집중국을 배치할 때, 각 집중국의 수신 가능 영역 길이의 최소합을 구하여라
  • 센서의 좌표 값은 음수일 수도 있다.
  • 집중국의 개수가 센서의 개수보다 많지는 않다.
  • 일부 센서들의 좌표가 동일할 수도 있다.

최종 코드

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		
		int N = Integer.parseInt(br.readLine());
		int K = Integer.parseInt(br.readLine());
		
		int[] s = new int[N];
		StringTokenizer st = new StringTokenizer(br.readLine());
		for (int i = 0; i < N; i++)
			s[i] = Integer.parseInt(st.nextToken());
		
		Arrays.sort(s);
		
		int[] dd = new int[N - 1];
		for (int i = 1; i < N; i++)
			dd[i - 1] = s[i] - s[i - 1];
		
		Arrays.sort(dd);
		
		int sum = 0;
		for (int i = 0; i < N - K; i++)
			sum += dd[i];
		
		System.out.println(sum);
	}
}

배운점

일단 문제를 이해하는 데 시간이 많이 필요했다.

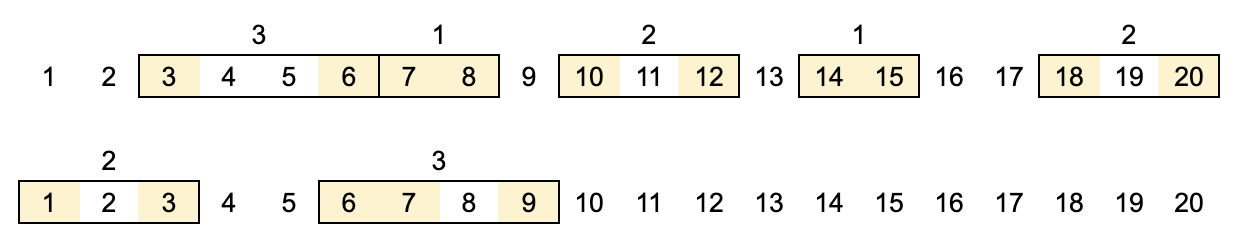
이런식으로 집중국이 커버하는 범위의 합이 가장 작도록 해야한다.

주어지는 숫자들로 여러 시도를 해보다가 규칙을 발견했다.

1. 센서 좌표 배열을 저장한다.
2. 센서 좌표 배열을 정렬한다. (가까운 좌표 ~ 먼 좌표)
3. 센서 간 거리를 배열에 저장한다.
4. 센서 간 거리 배열을 정렬한다. (간격 작음 ~ 간격 큼)
5. 거리 배열에서, 앞에서부터 합을 구한다. 단, N - K - 1번째 인덱스까지만 포함하여 처리한다. (K - 1개의 구간에 대한 합계)

그리디 알고리즘 익숙해지기

최적의 선택 : 가장 큰 거리 K-1개를 제거하여 최소한의 거리 합을 만드는 선택

1. 센서 위치 정렬
   Arrays.sort(s)를 통해 센서 위치를 정렬한다.

2. 센서 간 거리 계산
   인접한 센서 간의 거리를 dd 배열에 저장합니다.

3. 가장 큰 거리들 제거 (그리디)
   K개의 집중국을 설치하려면 총 K개의 구간을 형성해야 하므로, 센서 간 거리 중 가장 큰 K-1개를 제거하여 K개의 구간으로 나눌 수 있다.
   거리 배열 dd를 오름차순으로 정렬한 후, 가장 큰 K-1개의 거리만큼을 제외하고 나머지 작은 거리들만 합한다.

4. 최소 거리 합 계산
   가장 큰 거리 K-1개를 제거한 후 남은 거리 합 sum을 계산한다.

Kotlin code

import java.io.BufferedReader
import java.io.InputStreamReader
import java.util.StringTokenizer

fun main() {
    val br = BufferedReader(InputStreamReader(System.`in`))

    val N = br.readLine().toInt()
    val K = br.readLine().toInt()

    val s = IntArray(N)
    val st = StringTokenizer(br.readLine())
    for (i in 0 until N)
        s[i] = st.nextToken().toInt()
    s.sort()

    val d = IntArray(N - 1)
    for (i in 1 until N)
        d[i - 1] = s[i] - s[i - 1]

    d.sort()

    var sum = 0
    for (i in 0  until N - K)
        sum += d[i]

    println(sum)
}