그래프는 인접행렬과 인접 리스트로 구현될 수 있다.
인접 행렬
그래프에서 어느 노드들이 간선으로 연결되어 있는지를 나타내는 행렬이다. 구현 시에는 이차원 배열로 구현되며 노드 사이에 간선이 있다면 1, 없다면 0으로 표현한다.
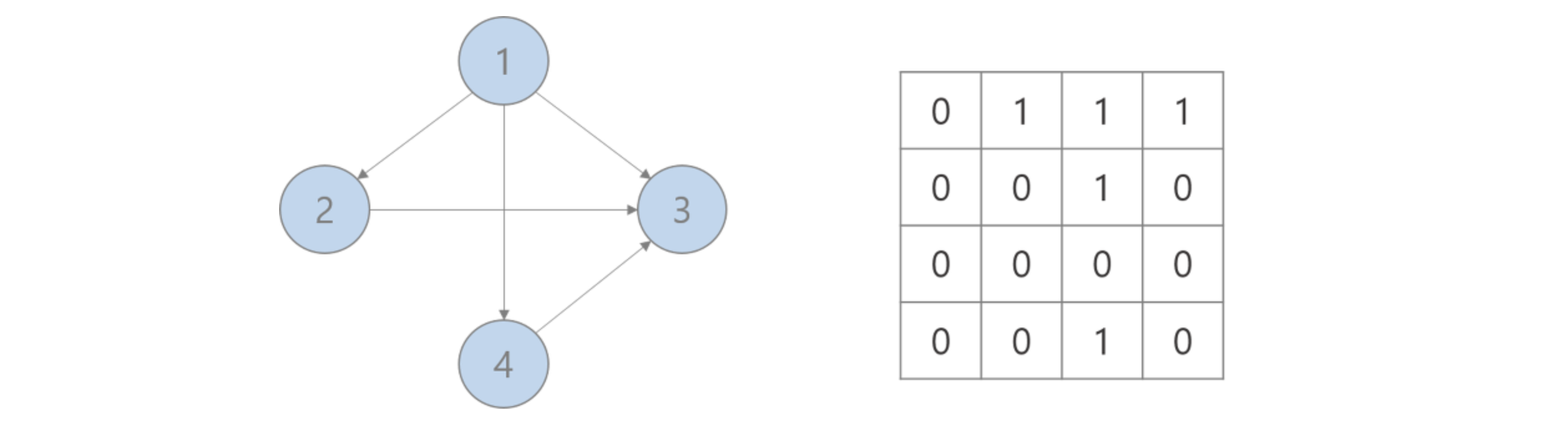
방향 그래프의 경우는 위의 사진과 같이 표현이 된다. 노드 1은 노드 2와 노드 3, 노드4로 가는 경로가 있으므로 [0, 1, 1, 1]로 표현되며 노드 2는 노드 3으로 가는 경로만 있으므로 [0, 0, 1, 0] 으로 표현된다. 위 그래프에는 자기 자신으로 가는 경로는 없으므로 대각선은 모두 0으로 표시된다.
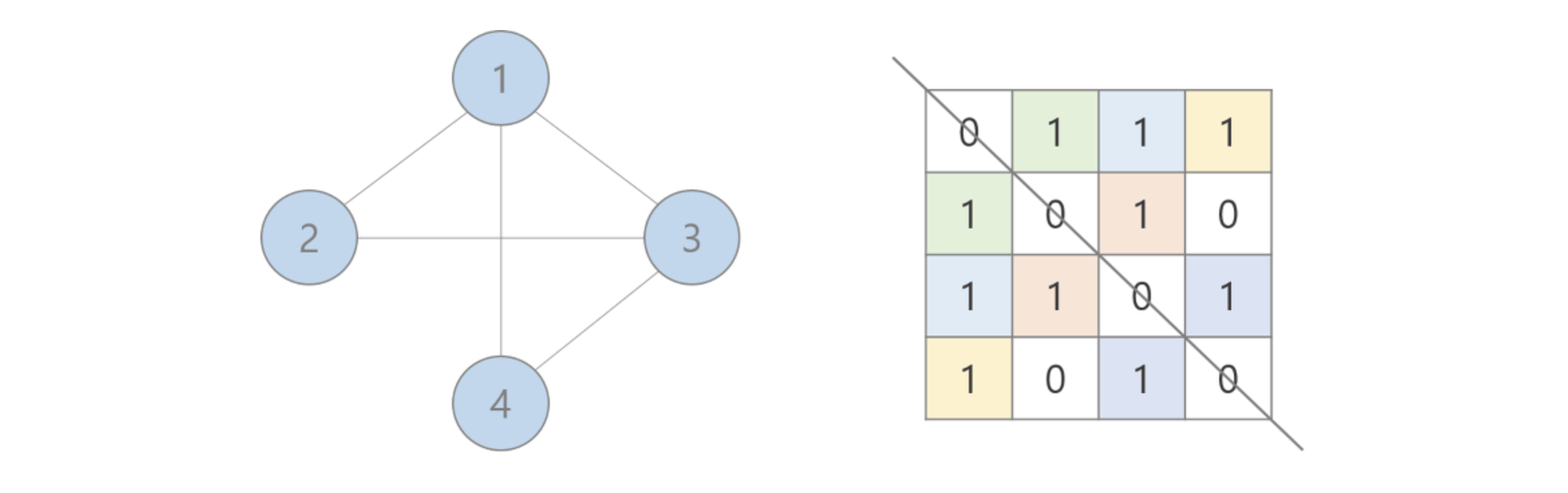
다음은 무방향 그래프이다. 무방향 그래프에서는 노드 A, B 간 경로가 있을 때, (1, 2)와 (2, 1) 은 같은 것으로 취급하므로 인접 행렬에서도 대각선 원소를 기준으로 대칭 모양을 가진다.
1) 장점
그래프 구현 시 인접행렬을 이용하면 구현이 쉽고, 노드 간 연결 유무를 확인할 때 행렬에서 해당 위치의 값이 0인지, 1인지 확인하면 된다. 예를 들어, 인접 행렬 adj가 있을 때 노드 i와 노드 j 연결 유무는 adj[i][j] 원소를 확인하면 알 수 있다. 따라서 시간 복잡도는 O(1)의 시간이 소요된다.
2) 단점
노드의 수가 v개일 때, 노드 i에 연결된 모든 노드를 방문해야한다면 v개의 노드 중 연결된 노드는 단 2개더라도 adj[i][0] 부터 adj[i][v] 까지 모두 연결 관계를 확인해야하기 때문에 O(v) 의 시간이 소요된다.
3) 구현 (무방향 그래프)
import sys
input = sys.stdin.readline
v = int(input())
e = int(input())
adj = [[0 for _ in range(v)] for _ in range(v)]
for _ in range(e):
idx, edge = map(int, input().split())
adj[idx-1][edge-1] = 1
adj[edge-1][idx-1] = 1
print(adj) # [[0, 1, 1, 1], [1, 0, 1, 0], [1, 1, 0, 1], [1, 0, 1, 0]]인접 리스트
인접 리스트란 각 노드에 연결된 노드들을 원소로 갖는 리스트들의 배열을 의미한다. 따라서 인접 리스트 adj가 있다면 adj[i]는 i번 노드에 연결된 노드들을 원소로 갖는 리스트이다.
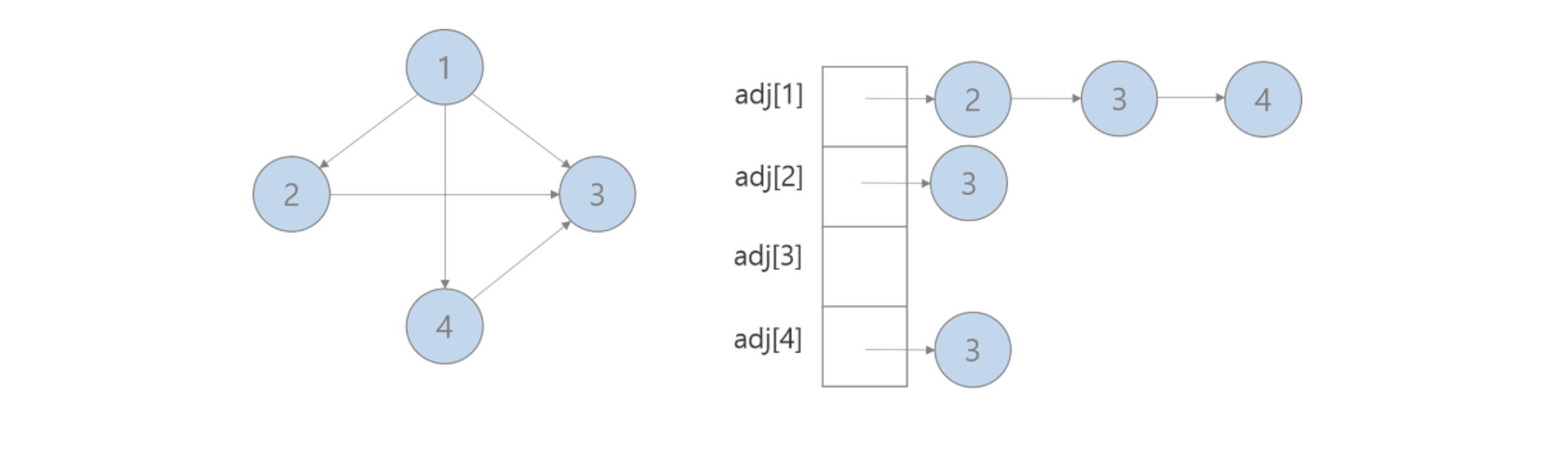
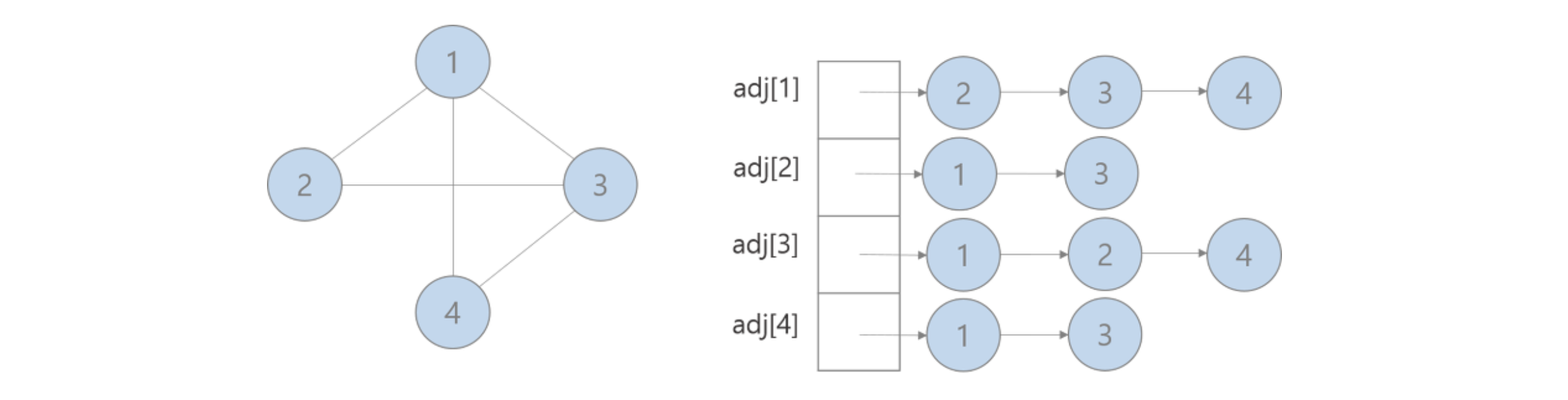
위 예시로 들었던 그래프를 인접 리스트로 나타내면 위 그림과 같이 표현될 수 있다. 1번 노드는 2, 3, 4번 노드로의 간선으로 연결되어있으며 2번 노드는 3번과, 4번 노드는 3번 노드로의 간선으로 연결되어있음을 알 수 있다. 무향 그래프를 인접 리스트로 표현하면 다음과 같이 표현될 수 있다.
1) 장점
인접 행렬은 모든 노드를 표현하고 각 노드의 연결 상태를 나타내는 반면 인접 리스트는 실제로 연결된 노드들만 저장하기 때문에 간선의 개수와 비례하는 만큼만 메모리를 차지한다. 따라서 인접 행렬보다 탐색에서 더 효율을 보인다.
2) 단점
반대로 인접 리스트는 노드 i와 노드 j와의 연결 상태를 확인하려면 adj[i]의 리스트를 순회하며 노드 j가 포함되어 있는지 확인해야한다. 이 경우 인접행렬은 adj[i][j]가 0인지 1인지를 확인하면 되는 반면 인접 리스트는 O(v)의 시간복잡도를 갖는다.
3) 구현 (무방향 그래프)
import sys
input = sys.stdin.readline
v = int(input())
e = int(input())
adj = [[] for _ in range(v)]
for _ in range(e):
a, b = map(int, input().split())
adj[a-1].append(b-1)
adj[b-1].append(a-1)
print(adj) # [[1, 2, 3], [0, 2], [0, 1, 3], [0, 2]]마무리
이렇게 그래프를 구현하는 두 가지 방법에 대해 알아보았다. 각 방법은 경우에 따라 적합한 사용 케이스가 있다. 예를 들어 인접행렬은 노드들의 연결 상태를 확인해야하는 경우나 간선으로 연결된 노드들이 많은 경우에 적합하며, 노드는 많지만 간선의 수는 적은 희소 그래프이거나 연결된 노드를 탐색해야하는 경우에 적합하다. 이렇게 그래프를 어떻게 활용할지에 따라 더 적합한 방법을 선택하면 되겠다.
참고
https://sarah950716.tistory.com/12
https://devuna.tistory.com/32
