문과생이 적어보는 백트래킹(재귀와 DFS 를 곁들인)
들어가기에 앞서서, 해당 글은 기본적인 문법 (for, while, print, 입력받기, 배열)에 대해서 알고 있음을 전제로 합니다.
만약 기본적인 문법을 모르는 상태라면 반복문과 출력, 배열, 입력받기에 대해서 먼저 이해한 후 다시 찾아와주세요. :)
이 글은 백트래킹만 언급하는 것이 아니라 재귀함수부터 백트래킹까지 모든 내용을 차례대로 다룹니다.
그 과정에서 약간의 자료구조(Stack), 명령형 프로그래밍과 선언형 프로그래밍의 차이, DFS 를 재귀로 구현하는 이유 등에 대해서 언급합니다.
예제에서 C언어와 Kotlin 을 섞어서 사용하고 있지만, 최대한 언어적 특징없이 기본적인 문법만 사용합니다.
글은 작성자가 이해한 흐름에 따라 작성되었으며, 의식의 흐름에 따라 작성되어 존대없이 편한 말로 작성되었습니다.
오류 및 오타 지적 감사합니다. :)
작성자 : 뉴원(Newon)
백트래킹, DFS 탐색 중 가지치기 하는 것.
백트래킹은 완전 탐색 방법 중 하나인 깊이 우선 탐색(DFS)을 진행하면서 조건을 확인,
해당 노드가 유망하지 않으면 더 이상 탐색하지 않는 것을 의마한다.
백트래킹은 일반적으로 재귀의 형태로 작성되며, 크게 다음의 3개 내용을 작성해야한다.
- 재귀를 진행하는 동안 사용될 깊이(depth)를 매개변수로 넣기
- 재귀가 종료되는 시점에서 수행해야할 내용
- 재귀가 진행중이면 가지치기(백트래킹)할 내용
여기에 재귀함수를 편하게 돌리고 싶다면 재귀에 필요하지만 변하지 않는 변수들과 재귀에서 사용하는 배열들을 전역변수로 선언하면
재귀함수의 매개변수가 깔끔해져서 편하다.
코드로 확인해보자. 백준 N과 M(1) 문제 를 확인하면
1 ~ N 까지의 숫자 중에서 M개를 중복없이 오름차순으로 출력하는 것이 문제이다.
코드는 C언어로 쓰였지만, 코드만의 특징없이 작성되었다.
// 목표 : 1 ~ N 까지의 숫자에서 M개르 선택하고 중복없이 오름차순으로 출력하기
#include <stdio.h>
#include <stdbool.h>
int arr[10] = {0, }; // 1부터 N까지이니, 마음편하게 10개의 배열을 선언하였다.
bool isusedArr[10] = {false,}; // 해당 숫자의 중복 여부를 위해 사용했는지 안했는지를 파악할 같은 크기의 배열을 하나 더 선언했다.
int N; // 재귀에서 사용하지만 그 숫자가 변하지는 않는 변수를 전역변수로 선언하였다.
int M; // 재귀에서 사용하지만 그 숫자가 변하지는 않는 변수를 전역변수로 선언하였다.
void Solve(int k){ // 재귀함수가 사용되는 동안 사용될 depth 를 여기선 k로 표현하고 있다.
if(k == M){ // 해당 재귀함수는 k가 계속 증가하며, k == M 일때 멈추는 구조를 가지고 있다.
for (int i = 0; i < M; i++){ // 종료될 때, 수행해야할 내용은 "출력"이므로, 출력을 하고 있다.
printf("%d ", arr[i]);
}
printf("\n"); // 엔터를 출력하고 있다.
return; // 마지막에 수행해야할 내용들을 다 수행했으면 return 으로 함수를 종료한다.
}
for (int i = 1; i <= N; i++){ // 재귀함수가 종료시점이 아니라면 for 문을 통해 재귀를 진행한다.
if(!isusedArr[i]){ // 가지치기할 내용을 찾고있다. 이번 같은 경우는 중복을 없애기 위해 다음과 같이 적용하고 있다.
arr[k] = i; // arr[k] 에 i를 사용하고 있다.
isusedArr[i] = true; // 사용하니까, 사용했음을 표시하고 있다.
Solve(k+1); // 여기에서 재귀가 계속 반복되고 있다. k는 자릿수로 계속 증가하다가, k == M일 때 종료돨 것이다.
isusedArr[i] = false; // 다음 DFS 를 위해 다시 사용하지 않았으로 바꿔주고 있다.
}
}
}
int main(){
scanf("%d %d", &N, &M); // 함수의 시작이다. N과 M을 입력받고 있다.
Solve(0); // 재귀함수의 시작이다. 0부터 시작하고 있다.
}코드를 크게크게 확인해보자
- Solve 함수는 DFS 함수로 k를 기준으로 진행되고 있다.
- Solve 의 맨 위에선 재귀가 종료될 시점에 출력을 하고 변경없이 return 으로 함수를 종료하고 있다.
- Solve 의 밑 에서는 for 문을 통해 가지치기할 내용을 확인하고 있다.
if(!isusedArr[i])를 통해 isusedArr이 0, 즉 사용하지 않은 숫자라면 재귀를 진행하고 있다.
세부적으론,arr[k]에 i를 넣고있고, 해당 i를 사용처리 한 후 다음 재귀로 넘어가고 난 후 비사용으로 바꿔주고 있다.
백트래킹은 위의 구조를 기본 골조로 하며, 조건의 추가 & 삭제, 혹은 해당 depth 의 사용, 미사용 등의 조합으로 사용된다.
아 그래서 그게 뭔데 ㄹㅇㅋㅋ

만약 당신이 위의 글만 보고서 아 ! 백트래킹이란 저런거구나 ㅎㅎ 이해했어 라면 이제 뒤로가기를 눌러도 좋다.
이제부터 이 글은 철저하게 아무것도 모르는 문과생의, 문과생에 의한, 문과생을 위한 언어로 설명된다.
우선 우리는 ① 재귀함수가 무엇인지 정확하게 알 필요가 있다.
그 다음으로 ② DFS 함수에 대해서 알아야 하며,
최종적으로 DFS 를 진행할 때 ③ 가지치기(백트래킹)을 어떻게 하는 지 알아볼 것이다.
① 재귀함수가 뭔데
가. 재귀함수란?


재귀함수란 코드 내에서 자기 자신을 호출하는 함수를 의미한다.
내가 나를 부르고, 다시 내가 나를 부르고, 틱X 이나 유튜브숏X에서 자주 보던 그것들이 맞다.
프로그래밍으로 재귀함수는 다음처럼 쓰인다.
fun DFS(N: Int){
print("$N ")
return DFS(N + 1);
}
fun main(){
DFS(0)
}위의 코틀린 함수를 확인해보자.
main 함수에서 DFS라는 함수를, 0을 넣어서 호출하고 있다. 함수 이름에는 우선 신경쓰지 말자
DFS 라는 함수가 뭐하는 녀석인지 확인해보면, 우선 이녀석은 N을 매개변수로 받고 있다.
이후 print("$N ") 을 통해서 N과 스페이스바를 출력하고, 종료할 때 자기 자신에 (N+1)을 넣은 것, DFS(N + 1) 을 호출하고 있다.
그렇다면 이 재귀함수는 어떻게 작동할까?
- DFS(0) 호출 - DFS(0)의 내용 수행 - DFS(0 + 1) 호출
- DFS(1) 호출 - DFS(1)의 내용 수행 - DFS(1 + 1) 호출
- DFS(2) 호출 - DFS(2)의 내용 수행 - DFS(2 + 1) 호출
- 무한반복
...
와 같이 반복하게 된다.
언제 끝날까? 영원히 끝나지 않는다. 왜냐하면 위의 함수는 자기자신을 호출하곤 있지만, 종료 조건이 없기 때문이다.
따라서 위의 컴퓨터의 메모리가 허락할 때 까지
0 1 2 3 4 5 ... 백만스물하나 ... 백만스물둘...
을 출력하고 있을 것이다.

이 터미널 창을 DFS 함수라고 비유한다면, 다음과 같이 1을 받고 1 출력 종료 -> 2를 받고 2 출력 종료 ... 를 무한반복 중인 것이다.
위의 재귀함수를 다음과 같이 바꿔보자.
fun DFS(N: Int){
if(N == 11)
return;
printf("$N ")
return DFS(N + 1)
}
fun main(){
DFS(0)
}위의 코드와 차이점은 N이 11일 때, 아무것도 하지 않고 그냥 종료가 된다는 것이다.
그럼 이 함수는 다음과 같이 작동한다.
- DFS(0) 호출 - N이 11인지 확인 - 11이 아님 - DFS(0)의 내용 수행 - DFS(0 + 1) 호출
- DFS(1) 호출 - N이 11인지 확인 - 11이 아님 - DFS(1)의 내용 수행 - DFS(1 + 1) 호출
- DFS(2) 호출 - N이 11인지 확인 - 11이 아님 - DFS(2)의 내용 수행 - DFS(2 + 1) 호출
... - DFS(11) 호출 - N이 11인지 확인 - N이 11임 - 그냥 종료
if 문에서 N이 11일 때 종료하라는 내용을 통해서, 해당 재귀함수는 무한반복하지 않고 N이 11일 때 바로 종료하게 된다.
따라서 위의 코드는 다음과 같이 출력하고
0 1 2 3 4 5 6 7 8 9 10
이후 함수가 종료된다.
if 문을 통해서 재귀함수가 종료될 조건을 단 것, 이것을 Base Condition 이라고 부른다.
재귀함수는 매개변수를 통해서 Base Condition 에 점차 다가가도록 설계하는 것이 원칙이다.
그래야 재귀함수를 안전하게 종료시킬 수 있기 때문이다.
매개변수는 Base Condition 에 다가갈수만 있다면 증가해도, 감소해도 상관없지만 일반적으로 감소하도록 설계한다.

이 짤방을 다시 한번 살펴보자, 모든 함수는 return을 기준으로 종료하게 되어있다. 그렇다면 기존에 불려진 함수들은 언제 종료가 될까?
정답은 호출된 순서의 역순으로 닫힌다 이다. 짤방으로 표현하자면 이렇게 된다.

그래서 코드를 이렇게 짜면, 역순으로 정렬할 수도 있다.
fun DFS(N: Int){
if(N == 11){
return;
}
DFS(N + 1)
print("$N ")
return;
}
fun main(){
DFS(0)
}위의 코드는 DFS 를 호출한 다음에 N을 print 하고 있다.
따라서 N 이 11까지 이른 다음에야 순차대로 종료되며 N이 10일 때, N이 9일 때, 8..7..
순서대로 출력되고 가장 마지막 == 가장 처음에 호출한 함수가 종료된다.
출력은 요렇게 나온다. -> 10 9 8 7 6 5 4 3 2 1 0
이 의미가 이해되었다면 재귀함수란? 에 가장 먼저 나왔던 2개의 짤 중 밑의 짤방이 전부 이해될 것이다.
이러한 방식을 자료구조 중 `Stack` 이 적용된 것 이라고 한다. `
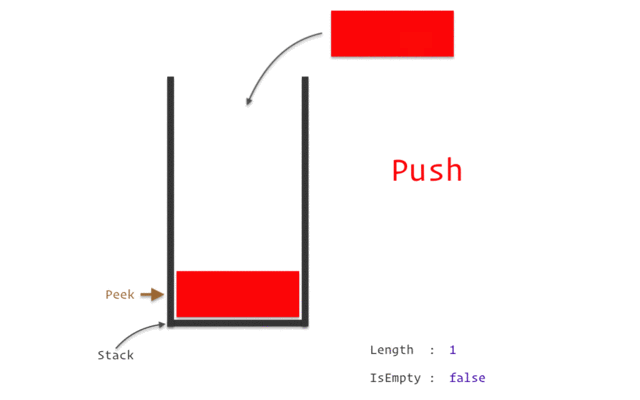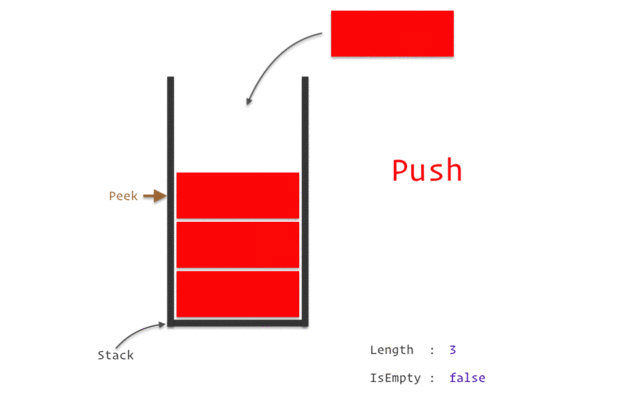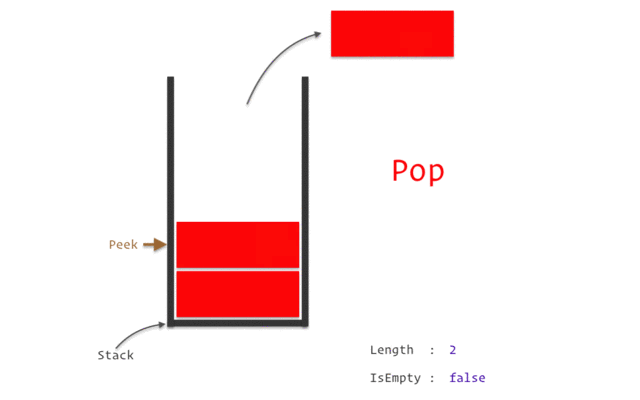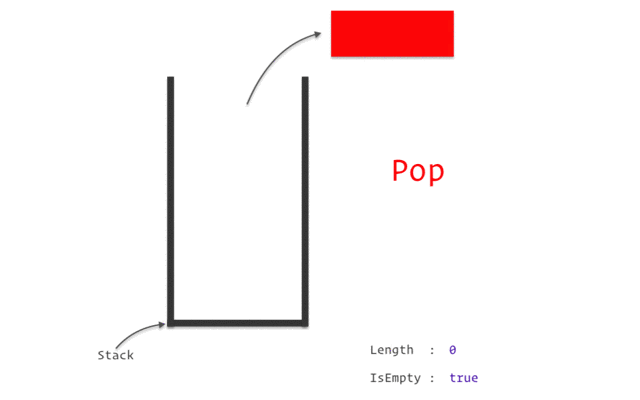
설명에서 push 는 자료 삽입을, pop은 자료를 빼는 것을 의미하며
스택 구조가 적용되면 데이터는 언제나 마지막에 넣은 것부터 빼내게 되고, 처음에 넣은 것 이 가장 마지막에 나오게 된다.
재귀, DFS, 백트래킹이 전부 Stack 이 적용되지만 본 글에서는 이 이상의 Stack 개념은 사용하지 않는다.
궁금하거나 필요하다면 Stack 을 찾아보는 것을 추천한다.
어 음 그런데 말이죠 ..?

사실 위의 출력문들은 굳이 재귀로 하지 않고, for 문으로도 쉽게 만들 수 있다.
for(i in 0..10){
print("$i ")
}
// 역순이면 이렇게
for(i in 10 downTo 0){
print("$i ")
}게다가 하나의 함수를 호출하는 것은 단순한 중복문보다 많은 메모리를 요구하며 속도 역시 압도적인 힘ㅇ.. 느리다.
이러한 이유에도 불구하고 재귀함수를 쓰는 이유를 알아보자.
나. 메모리도 많이 잡아먹고 헷갈리는 재귀함수 왜 씀? (Feat. 선언형 프로그래밍)
코드란 컴퓨팅 효율적으로만 설계하는 것이 아니라
이후 타인에 의한 유지 보수를 고려하여 적어야 한다.
즉 누가 보더라도 코드는 쉽게 읽히며, 코드가 수행하는 내용이 직관적이여서 개발자의 작업시간을 줄이는 것
또한 좋은 코드의 조건 중 하나이다.
이러한 관점에서 재귀함수는 for 문으로 작성했을 때 보다 월등히 가독성이 높아서, 개발자의 시간을 줄여줄 수 있을 때 사용한다.
재귀함수가 직관적이라니, 이게 무슨소리일까?
피보나치의 수열을 예시로 들어보자.
수학에서, 피보나치 수(영어: Fibonacci numbers)는 첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열이다.
1 1 2 3 5 8 13 21 34 55 ...
이걸 For 문과 재귀함수로 구현하면 다음과 같다.
// for 문으로 작성한 피보나치
fun Fibonacci(N: Int): Int{
var one = 1
var two = 1
var result = 0
if(N <= 2){
print("$one ")
return;
}
for (i in 3..N){
result = one + two
one = two
two = result
}
return result
}
// 재귀로 작성한 피보나치
fun Fibonacci(N: Int): Int{
if(N == 0)
return 0
if(N == 1)
return 1
return Fibonacci(N - 1) + Fibonacci(N - 2)
}
fun main(){
print(Fibonacci(10))
}
// 출력은 같은 10이다.잠시 저 두 함수가 피보나치를 출력한다는 것을 모른채로 비교해보자.
For 문으로 적힌 함수를 이해하려면 one 이 어떤 변수인지, two 가 어떤 변수인지, result 는 어떤 변수인지
N 이 왜 2일땐 one만 출력하고 리턴하는지, for문은 왜 3부터 시작하고 그때마다 result 는 one + two 를 받는지 이해하고나야 비로서
이 함수가 피보나치 함수임을 이해할 수 있다.
그에 반면 재귀로 작성된 함수는 간단하다.
계산이 어떻게 되는진 모르겠지만 함수(N) 은 함수(N-1) + 함수(N-2) 이고,
이걸 계속해서 반복하다보면 N 이 0일 땐 0을, N이 1일 땐 1을 리턴하여서 이를 반복한다고 적혀있다.
더 간단하게는, 내부가 어떻게 돌아가는진 모르겠지만 우린 함수(N) = 함수(N-1) + 함수(N-2) 임을 알 수 있다.
이것이 재귀함수를 사용했을 때 가독성이 늘어나는 대표적인 사례이다.
피보나치 수열은 그나마 2개의 항이 만드는 상황만 이해하면 되었지만, 이보다 더 복잡한 사례가 나온다면 For 문으로 작성된 함수는 더더욱 힘들 것이다.
바로 그런 사례가 있다.
재귀함수를 구글링했다면 바로 접해봤을 문제, 하노이의 탑 문제이다.

간략히 요약하면, 3개의 대가 있고 크기가 오름차순인 원반들이 있고, 이걸 한번에 하나씩 옮겨서 다른 대로 옮기되,
큰 원반은 작은 원반 위에 갈 수 없다 는 조건 속에서 수행하라는 것이다.
알고리즘 문제로 치환하자면 원반이 움직일 때 마다 어디서 어디로 옮겼는지 출력하고, 최종적으로 몇번 움직였는지 출력하라 정도로 바꿀 수 있겠다.
For 문으로 도전.. .
도전은 언제나 아름답지만, 이번엔 추천하진 않는다.
For 문으로 만들고 싶다면 우선 원반의 갯수만큼 For 문을 만들어야할 것이며, 한번 옮겨질 때 마다 이전의 For 문들은 어떻게 해야하는지,
횟수는 어디에서 세야할 지도 막막한데, 원반의 갯수가 N으로 입력받아야 한다면 ..

여기서 우리는 재귀함수의 진정한 사용이유를 알 수 있다.
재귀함수의 가장 큰 장점은 For 문과 같은 명령형 프로그래밍이 아니라, 선언형 프로그래밍이라는 점에 있다.
무슨 의미일까?
잠시 하노이의 문제는 접어두고, N 팩토리얼을 한번 출력해보자.
알다시피, 방법은 For 문과 재귀함수 2개가 있다.
팩토리얼이란 N을 기준으로 n부터 1까지의 모든 수를 곱한 값이다. (표기는 n!)
이때 명령형 프로그래밍의 관점에서 10!을 구하려면 다음과 같이 바라보게 된다.
var value = 1
for (i in 1..10){
value *= i
}
----------------
value = 1 * 2
value = (1 * 2) * 3
value = (1 * 2 * 3) * 4
...
value = (1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9) * 10- value 에 대하여 사용자는 모든 i 항들에 대하여 절차적으로 구하고 나서야 팩토리얼 n을 알게되는 것으로
인식한다.
이를 다시 선언형 프로그래밍 관점에서 바라본다면 다음과 같아진다.
fun Factorial(N: Int): Int{
if(N == 1) return 1
return Factorial(N - 1) * N
}
----------------
N == 10 Factorial(9) * 10
N == 9 Factorial(8) * 9
N == 8 Factorial(7) * 8
...
N == 2 Factorial(1) * 2
N == 1 1- 재귀함수 Factorial 은 return 값이 재귀함수와 어떤 관계가 있는지
선언만 하였다. - 그 이후 절차에 관련한 것은 return 을 수행하는 컴퓨터에게
맡겨버리고사용자는선언에 해당하는 결과값을 갖는 것으로인식한다.
같은 결과값이지만 명령형 프로그래밍의 관점은 사용자가 모든 절차를 인지하고 있음을 전제하는 반면
선언형 프로그래밍의 관점은 사용자가 결과와 그 나머지의 관계를 선언만 한다는 점에서 차이가 나타난다.
즉, 재귀함수의 장점 중 하나는 계산에 대한 내용을 컴퓨터에게 맡겨버린다에 있다.
이를 하노이에 적용시켜보자.
문제를 한정시켜서, N개의 원판과 대 A, B, C 가 있을 때 원판들은 최초에 A에 있고, N개의 원판을 C로 옮기는 것을 목표로 한다.
하노이의 탑 문제의 답을 거꾸로 추적해보면 다음과 같은 특성을 지닌다.
- 가장 마지막의 원판을 제외하고, N - 1 개의 원판들을 B에 옮겨놓는다.
- 마지막 원판을 C에 갔다 놓는다.
- B에 옮겨놨던 원판들을 C에 통째로 옮긴다.
이걸 역순으로 반복하면 우리가 게임 에서 진행했던 순서가 된다.
// C로 작성되었다.
// 대의 이름은 각각 A, B, C 이며 N개의 원판이 있는 상황이다.
#include <stdio.h>
int N;
int count;
void Hanoi(int N, int A, int B, int C){
// N 이 0 일때가 Base condition 이지만 이번 경우엔 수행해야할 내용이 없으므로, 적지 않았다.
if(N > 0){ // N 이 0이 아닌동안, 즉 Base Condition 에 도달하지 않는 동안 수행할 내용이다.
Hanoi(N-1,A,C,B); // A에 있는 N - 1개 원판들을 C를 이용해서 B로 옮긴다.
printf("%d 에서 %d 로 가장 맨 위의 원판 이동\n", A,C); // A에 있는 남아있는 원판, 가장 큰 원판을 C로 옮긴다.
Hanoi(N-1,B,A,C); // B에 있는 N - 1개 원판들을 A를 이용해서 C로 옮긴다.
}
}
int main(){
scanf("%d", &N);
Hanoi(N,1,2,3);
}이 함수에서 개발자는 절차마다 그 값이 무엇인지에 대해서 작성한 코드는 단 1개도 없다.
개발자는 그저 N - 1 일 때 어떻게 해야하는지 논리적으로 선언만 하였고, 컴퓨터가 대신 계산한 것이다.
이것이 재귀함수를 이용하는 이유이다.
위의 내용이 이해가 안간다면 다음의 영상을 참고하면 좋을 것 같다.Tower of Hanoi Problem - Made Easy
위의 하노이와 관련된 내용은 참고에 연결된 유튜브 영상의 내용을 요약하여 옮긴 것이다.
컴퓨터에 맡겨버린다 라는 의미가 궁금하다면 다음 블로그를 참고해보자. 반복과 재귀 : DFS 문제를 재귀로 구현하면 편리한 이유
재귀함수편 요약
- 재귀함수란 자기 자신을 호출하는 함수이다.
- 재귀함수는 매개변수를 통해 Base Condition 에 도달하도록 설계한다.
- 모든 재귀함수는 이론적으로 For문이나 While 문으로 구현이 가능하나, 사용자의 편의(가독성)를 위해서 사용된다.
재귀함수는 다이나믹 프로그래밍에서 다시 한번 쓰이게 된다.
② DFS 함수
이제 본론이다. 백트래킹은 뭐길래 DFS와 함께 쓰이는 걸까?
한줄 요약하자면 DFS 를 하는 와중에 더 이상 탐색할 필요가 없는걸 쳐내는 행위를 백트래킹이라고 한다.
DFS(Depth - First - Search) 는 깊이 우선 탐색을 의미한다.
어떠한 내용을 완전 탐색(브루트 포스)해야 할 때, 깊이 먼저 탐색하는 것을 의미한다.
그리고 우린 이 DFS 를 여태 실컷 살펴보았던 재귀를 통해 구현할 것이다.

DFS는 그래프나 트리와 연계되어 사용되지만, 본 글에서는 그래프나 트리의 내용 없이 DFS 그 자체에 대해서만 알아본다.
완전 탐색(브루트 포스)라는 개념이 생소하다면 본 글에서는 모든 걸 다 탐색한다 정도로 인지하면 된다.
DFS는 완전탐색 중 하나이니, 모든걸 탐색해야하는 상황을 가정해보자.
1부터 6까지의 숫자 중에서 3개를 뽑는 모든 경우의 수를 출력해보고자 한다.
여러가지 방법이 있겠지만 우린 다음과 같은 방법을 써보고자 한다.

목표 출력 예제는 다음과 같다.
1 1 1 | 수행 로직
1 1 2 | ① 3개의 빈칸을 만든다.
1 1 3 | ② 첫번째 자리에 1을 넣어본다.
1 1 4 | ③ 두번째 자리에 1를 넣어본다.
1 1 5 | ④ 세번째 자리에 1을 넣어본다
1 1 6 | ⑤ 세번째 자리에 1을 빼고, 2를 넣어본다.
1 2 1 | ⑥ 6까지 반복하고 나면, 두번째 자리를 2으로 바꾼다.
1 2 2 | ⑦ 세번째 자리를 1부터 채워넣는다.
... | ⑧ 6 6 6 가 될때까지 반복한다.
6 6 4 |
6 6 5 |
6 6 6 | 재귀함수로 구성할 것이며, 미리 코드를 보기 전에 고민해보는 것도 좋다.
코드는 다음과 같다.
#include <stdio.h>
int arr[3]; // 빈칸을 전역변수로 선언하여 함수가 호출할 때 마다 넣어주는 번거로움을 줄였다.
int N, M; // 문제에선 6개 중 3개이지만, 언제든 입력값에 따라 바꿀 수 있게 N과 M으로 설정했다.
// 여기서는 각각 6과 3으로 직접 하드코딩하지만 밑의 예제는 N과 M으로 넣는다.
void DFS(int depth){ // 이 재귀함수는 depth 를 기준으로 움직인다. 따라서 Base Condition 도 depth 를 기준으로 작성된다.
if(depth == 3){ // depth == 3일 때가 Base Condition 이다.
for(int i = 0; i < 3; i++){ // 배열에 쌓인 내용을 출력하고 있다.
printf("%d ", arr[i]);
}
printf("\n");
return;
}
for(int i = 1; i <= 6; i++){ // Base Condition 이 아닐때 for문을 돌며 후보군(1 ~ 6)을 찾고 있다.
arr[depth] = i; // 후보군을 찾으면 배열의 빈 칸에 넣고 있다.
DFS(depth + 1); // 다음 깊이로 넘어가고 있다.
}
}
int main(){
scanf("%d %d", &N, &M); // N과 M을 받고 있다.
DFS(0); // DFS를 0의 깊이부터 선언하고 있다.
}DFS 재귀함수는 0부터 시작하고 있으며,
배열의 인덱스 0 1 2 를 하나의 깊이로 인지하고, 0 -> 1 -> 2의 형태를 취하고 있다.
따라서 DFS 가 전달받는 depth 는 배열의 왼쪽부터 순서대로 탐색하게 된다.
그렇게 DFS 는 1부터 6까지 3개의 숫자를 넣는 방법을 중복을 포함해서 전부 넣고있다.

이것이 DFS 다.
깊이를 설정하고, 해당 깊이에 A가 있음을 상정하고, 다음 깊이로 가서 해당 깊이에 있을 수 있는 것을 다시 넣고 !!
하지만 출력문을 보니 좀 불편하다.
모든걸 깊이대로 탐색하는건 좋은데 중복도 없애고 싶고, 오름차순으로 정렬하고 싶은 마음이 들 수도 있다.
그걸 수행하는 것이 바로 백트래킹이다.
③ 백트래킹
위의 문제를 다시 한번 바꿔보자.
이번에는 1부터 6까지의 숫자 중에서 3개를 뽑되,
중복은 허용하지 않으며 오름차순으로 정렬할 것이다.
그림으로 표현하자면 다음과 같아진다.

목표 출력 예제는 다음과 같다.
1 2 3 | 수행로직
1 2 4 | 3개의 빈칸을 만든다.
1 2 5 | 첫번째 자리에 1을 넣어본다.
1 2 6 | 두번째 자리에 2를 넣어본다.
1 3 4 | 세번째 자리에 3을 넣어본다.
1 3 5 | 세번째 자리에 3을 빼고, 4를 넣어본다.
... | 6까지 반복하고 나면, 두번째 자리를 3으로 바꾼다.
3 4 6 | 세번째 자리를 3을 제외한 2~6까지 넣어본다.
3 5 6 | 4 5 6 가 될때까지 반복한다.
4 5 6 | 재귀파트에서 살펴보았던 것과 마찬가지로, 이걸 반복문을 통해서 만들수도 있겠지만 제법 많은 고생을 해야한다.
우리는 계산에 관한건 컴퓨터에 맡기고 선언으로 구현하고자 한다.
또한 조건에 부합하지 않는 것을 이제부터 유망하지 않다라고 표현한다.
#include <stdio.h>
int arr[M]; // 빈칸을 전역변수로 선언하여 함수가 호출할 때 마다 넣어주는 번거로움을 줄였다.
int visit[7] = {0, }; // 마찬가지 이유이다. visit 배열의 용도는 사용한 숫자인지 아닌지를 체크한다. 0 = 미방문, 1 = 방문
int N, M; // 문제에선 6개 중 3개이지만, 언제든 입력값에 따라 바꿀 수 있게 N과 M으로 설정했다.
void DFS(int depth){ // 이 재귀함수는 depth 를 기준으로 움직인다. 따라서 Base Condition 도 depth 를 기준으로 작성된다.
if(depth == M){ // depth == 3일 때가 Base Condition 이다.
for(int i = 0; i < 3; i++){ // 배열에 쌓인 내용을 출력하고 있다.
printf("%d ", arr[i]);
}
printf("\n");
return;
}
for(int i = 1; i <= N; i++){ // Base Condition 이 아닐때 for문을 돌며 후보군을 찾고 있다.
if(!visit[i]){ // 가지치기를 하고 있다, 방문한 곳은 가지 않고 있다.
arr[depth] = i; // 조건에 부합하면 빈 칸에 넣고 있다.
visit[i] = 1; // 가지치기를 위해 조건을 설정하고 있다, 방문한 곳을 방문했다라고 표현하고 있다.
DFS(depth + 1); // 다음 깊이로 넘어가고 있다.
visit[i] = 0; // 다음 단계를 위해 초기화해주고 있다.
}
}
}
int main(){
scanf("%d %d", &N, &M);
DFS(0);
}
//P.s. C언어에서 배열은 변수를 넣어 선언할 수 없어서, stdlib.h 의 동적할당 int* arr = (int*)malloc(sizeof(int) * M)) 을 사용해야하나
// 이해의 편의를 위해서 arr[M]을 넣었다.가장 상단에서 재귀함수에 필요하되, depth 가 아닌 것들을 전부 전역변수로 선언하였다.
DFS 재귀함수는 depth 라는 매개변수를 가지고서, Base Condition 에 도달하도록 조정되고 있다.
여기서는 depth 가 0부터 1씩 증가하며, Base Condition 이 3일 때 배열에 담긴 내용을 출력하고 종료되도록 설계되었다.
DFS 재귀함수에서 for문은 Baes Condition 에 도달하지 못했을 때 for 문에 들어가게 된다.
for 문에서는 후보군을 찾는 것과 동시에, 후보군을 찾더라도 방문하지 않은 곳 이라는 조건에 부합하지 않으면 유망하지 않으니 가지치기하고 있다.
유망하면 배열에 넣고, 방문처리를 한 후에, 다음 depth + 1 을 한 DFS를 호출함으로써 다음 깊이로 넘어가고 있다.
하나의 재귀함수가 Base Condition (depth == 3)에 도달하더라도
for 문에서 불려졌던 재귀함수들은 아직 종료되지 않았다.
DFS를 호출한 그곳으로 다시 돌아가서 방문처리 한 내용을 다시 미방문처리하고 (== 해당 깊이의 끝을 보아서 거슬러 올라가기),
for 문에서 다음 후보군을 찾고 다시 가지치기를 진행하고, 배열에 넣고, 유망한지 확인하고, 다음 깊이로 넘어가는 작업을 반복하고 있다.
또한 for 문은 계속해서 증가하게 되므로, 오름차순으로 자연스럽게 정렬이 된다.
이것이 깊이 우선 탐색에서 사용되는 백트래킹이다.
그래프와 트리의 개념없이 설명되었지만 사실 다음 깊이로 상정한 배열 을, 다음 노드로 바꾼다면 같은 맥락이 된다.
결론


여기까지 따라와주셔서 감사합니다 :) 이제 다시 한번 맨 위의 글을 보면 무슨 내용을 말했는지 완벽하게 이해가 갈 것이다. 여기까지 읽었다면 백트래킹을 좀 더 체화하기 위해서 [백준의 N과 M 시리즈](https://www.acmicpc.net/workbook/view/2052)를 전부 풀어보는 것을 추천한다. 설령 내용이 완벽하게 이해가 안 가더라도, 문제를 풀면서 자연스럽게 체화될 것이다. 그리고 N과 M을 전부 풀었다면, 당신은 그 악명높은 [N-Queen](https://www.acmicpc.net/problem/9663) 문제도 풀 수 있는 실력이 된 것이다. 화이팅 !
안뇽 ~ :)

참고
[자료구조] 스택(Stack)이란?
피보나치 수열
6. Recursion and Dictionaries
Tower of Hanoi Problem - Made Easy
반복과 재귀 : DFS 문제를 재귀로 구현하면 편리한 이유


우왕 .. 너무 어려워서 머리 싸매고 있었는데 읽고 한 번에 정리가 된 느낌이에요! 너무 감사합니다 ㅎㅎ