[백준]1654_랜선자르기.Kotlin

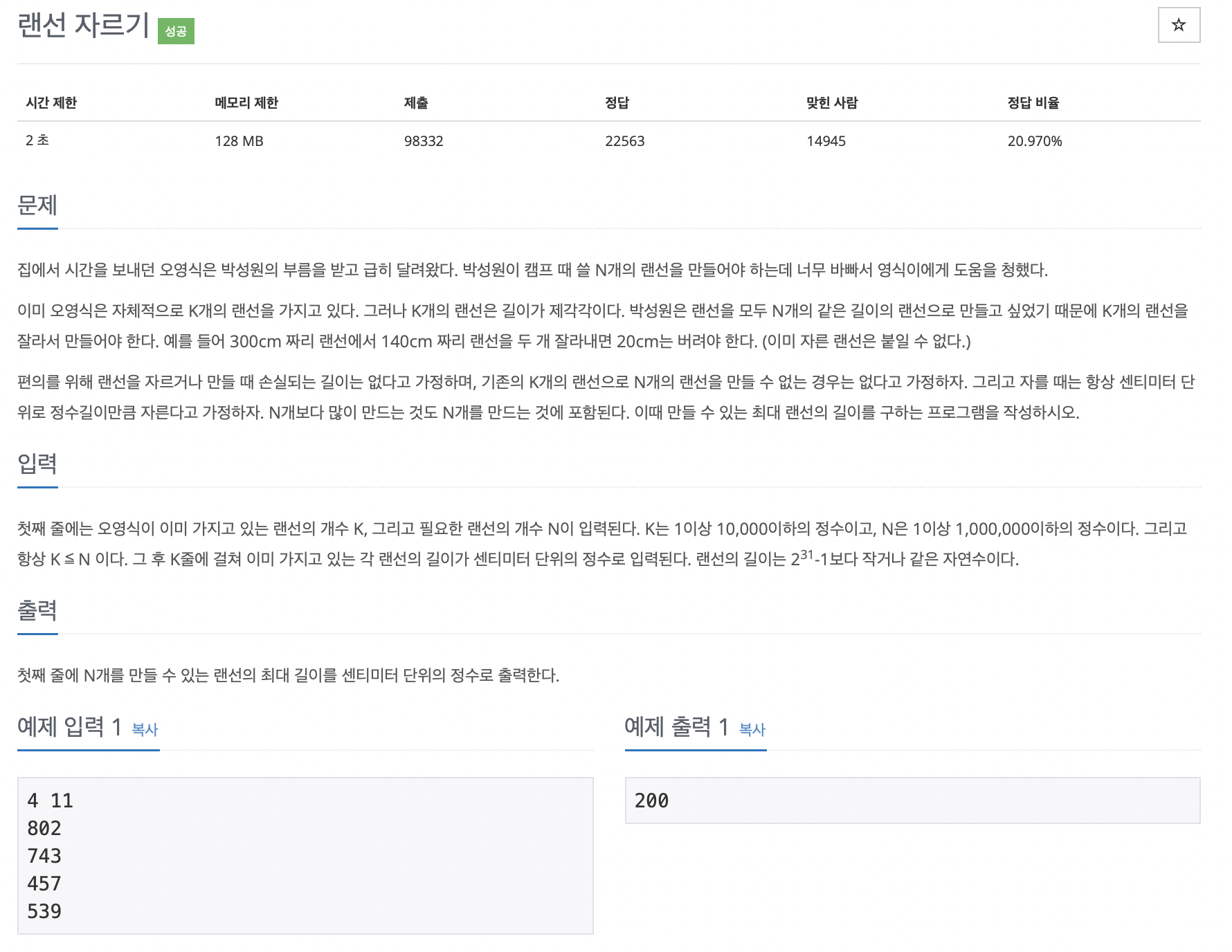
문제

문제로 이동하기

핵심 로직

• 이분 탐색으로 인덱스가 아닌 실제 값을 찾기
• 이분 탐색 중 Upper bound 를 활용하기

코드

lateinit var lanCable: Array<Int>  
  
fun solve(K: Int, N: Int): Long {  
    var minimumLan:Long = 0  
    var maximumLan:Long = lanCable[lanCable.lastIndex] + 1.toLong()  
    var mid: Long  
    var count:Long  
  
    while (minimumLan < maximumLan){  
        mid = (maximumLan + minimumLan) / 2  
        count = 0  
  
        for(i in lanCable.indices){  
            count += (lanCable[i] / mid)  
        }  
  
        if (count < N)  
            maximumLan = mid  
        else  
            minimumLan = mid + 1  
    }  
  
    return minimumLan  
}  
  
fun main() {  
    val br = System.`in`.bufferedReader()  
    val bw = System.`out`.bufferedWriter()  
  
    val (K, N) = br.readLine().split(" ").map {it.toInt()}
    
    lanCable = Array(K) { 0 }  
    
    for (i in lanCable.indices)  
        lanCable[i] = br.readLine().toInt()  
  
    lanCable.sort()  
  
    bw.append("${solve(K, N) - 1}")  
    bw.flush()  
    bw.close()  
}

풀이

랜선 자르기의 핵심은 여러 값들이 주어졌을 때, 문제의 조건을 만족하는 최댓값을 구하는 것이다.

비교를 해야할 여러 값들이 존재하고, 그 값들과 특정 조건이 만족하는 상황을 구하는 것인데 그림으로 표현하자면 다음과 같다.

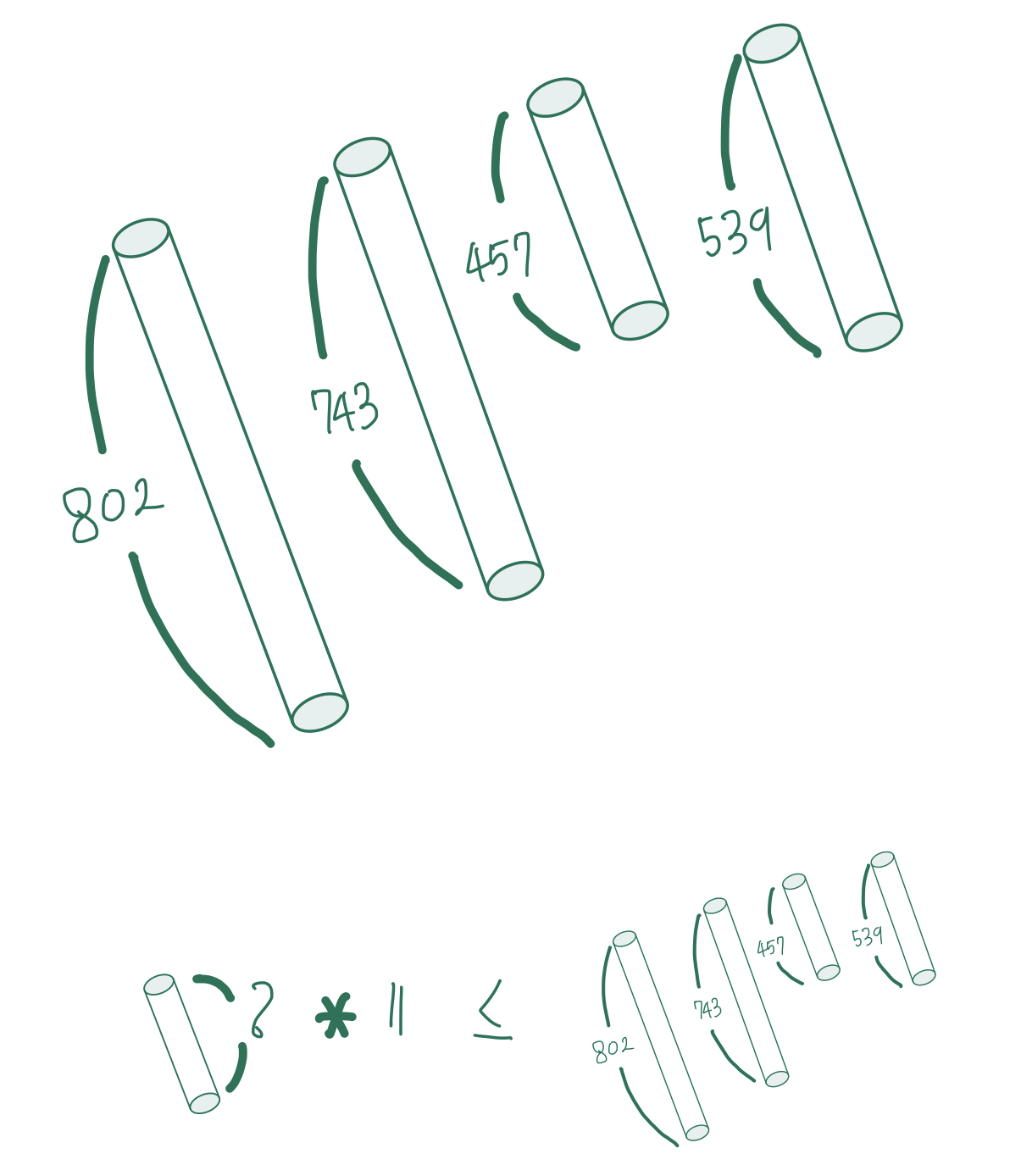
랜선 K (예제 입력 : 4) 개가 각각의 길이로 주어졌을 때,
각각의 랜선을 잘라서 N (예제 입력 : 11)개로 만들고자 하는데,
모든 랜선을 균일하게 자른다고 가정했을 때,
가장 길게 자를 수 있는 값은 무엇인가 ?

로 정리할 수 있다.

이때 일반적인 방법을 사용하면 시간초과를 받게 되고,
이분탐색 중 Upper bound 를 통해 보다 빠르게 찾아낼 수 있다.

원래의 이분탐색 중 Upper bound 는
중복이 있는 배열에서 중복의 가장 마지막 인덱스 값을 찾기 위해 사용된다.

fun binarySearch(arr: IntArray, target: Int): Int {
    var low = 0
    var high = arr.lastIndex
    var mid: Int

    while (low <= high) {
        mid = (low + high) / 2

        when {
            target < arr[mid] -> high = mid - 1
            target >= arr[mid] -> low = mid + 1
            // 찾고자 하는 값이 중앙값보다 크거나, *같다면(!!)*
            // 시작값(low)를 mid + 1 로 올려서
            // 만족하는 최대 인덱스를 찾는다.
        }
    }
    return low
}

하지만 이것을 조금 비틀어서
인덱스 대신 실제 값 으로 Upper bound 를 수행하는 것이 포인트다.

while (minimumLan < maximumLan){  
    mid = (maximumLan + minimumLan) / 2  
    count = 0  
  
    for(i in lanCable.indices){  
        count += (lanCable[i] / mid)  
    }  
  
    if (count < N)  
        maximumLan = mid  
    else  
        minimumLan = mid + 1  
}  
  
return minimumLan

여기서 count 는 랜선의 갯수를 세는 변수로,
조건에 부합한지 확인하는 변수이다.
위 코드의 target 역할을 한다.

주의사항

1. Int 범위를 넘어갈 수 있음.
   mid 를 구하는 방법이 (max + min ) / 2 이며,
   입력 상, max 와 min 을 합칠 때 Int 를 초과할 수 있으므로
   Long 을 써주어야 한다.
   
   
   
   
2. max 는 항상 max + 1 이어야 함.
   Upper bound 를 통해 찾는 값은
   min ~ max 내에서 찾게 된다.
   이는 특정 케이스, 최소와 최대가 0일 때 문제가 생긴다.
   

 min = 0
 max = 0
 mid = (min + max) / 2  // 0
 
 // min < max 가 아니기에, 
 // 이분탐색이 수행되지 않고 종료된다.

일반화 및 후기

해당 문제의 로직은 여러 값들 중에서 조건을 만족하는 최댓값을 구할 때 사용할 수 있다.

어려운 개념은 아닌데, 선뜻 손이 안 갔던 문제였다.