[JAVA/12851번] 숨바꼭질 2

문제

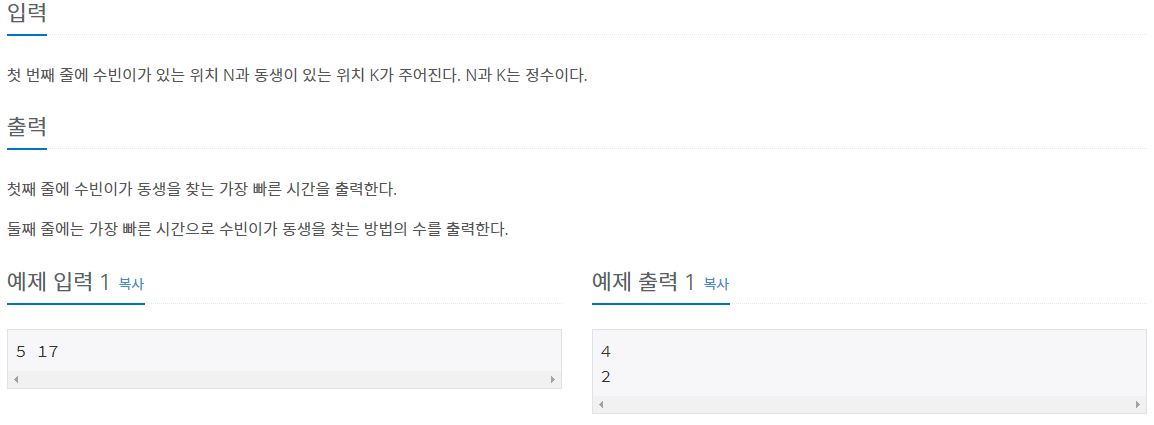
입력 및 출력

풀이

import java.io.*;
import java.util.*;

class Main {
    public static int N;
    public static int K;
    public static int[] map;
    public static boolean[] visited;
    public static int time = Integer.MAX_VALUE;
    public static void main(String args[]) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] temp = br.readLine().split(" ");

        // N, K(수빈이의 위치, 동생의 위치)
        N = Integer.parseInt(temp[0]);
        K = Integer.parseInt(temp[1]);

        // 수빈이와 동생의 위치가 같을경우 바로 리턴
        if (N == K) {
            System.out.println(1);
            return;
        }

        // 지도 데이터, 방문여부
        map = new int[100001];
        visited = new boolean[100001];

        // BFS메소드 호출
        BFS();
    }
    public static void BFS() {
        Queue < Node > queue = new LinkedList < > ();

        // 수빈이의 위치를 큐에 넣고 방문처리를 한다.
        queue.add(new Node(N, 0));
        visited[N] = true;

        // 구할 수 있는 경우의 수
        int count = 0;

        while (!queue.isEmpty()) {
            // 큐의 가장 앞에 있는 원소를 추출
            Node node = queue.poll();
            visited[node.pos] = true;

            // 최소시간보다 현재 노드의 시간이 커질 경우
            if (time < node.time) {
                System.out.println(time);
                System.out.println(count);
                return;
            }

            // 현재 위치가 동생의 위치와 같을 경우
            if (node.pos == K) {
                time = node.time;
                count++;
            }

            // 경우의 수는 총 3가지
            for (int i = 0; i < 3; i++) {
                if (i == 0) {
                    if (node.pos + 1 < 100001 && !visited[node.pos + 1]) {
                        queue.add(new Node(node.pos + 1, node.time + 1));
                    }
                } else if (i == 1) {
                    if (node.pos - 1 > 0 && !visited[node.pos - 1]) {
                        queue.add(new Node(node.pos - 1, node.time + 1));
                    }
                } else {
                    if (node.pos * 2 < 100001 && !visited[node.pos * 2]) {
                        queue.add(new Node(node.pos * 2, node.time + 1));
                    }
                }
            }
        }
    }
}
class Node {
    // 현재 위치와 걸린 시간
    int pos, time;

    // Node 생성자
    public Node(int pos, int time) {
        this.pos = pos;
        this.time = time;
    }
}

결과 및 해결방법

[결과]

[정리]

해결방법
이전에 풀었던 특정 지점에서 특정 지점을 찾아가는 문제와 유사했다. 그때 문제는 이차원 배열을 통해 해결하는 문제였다면, 이번 문제는 일차원 직선에서 해결하는 문제라고 생각하고 풀면 쉽게 풀 수 있다.

이 문제에서 사용할 수 있는 경우의 수는 총 3가지이다. {N + 1, N - 1, N * 2} 해당 조건을 토대로 반복문을 돌며 K지점에 도착하는 최소 시간을 구했다.

하지만 이번 문제에서는 최소 시간뿐만 아니라 다른 방법으로 최소시간에 도달하는 모든 경우의 수를 구해야하는 문제였다. 따라서 큐에 데이터를 넣을때 방문처리를 하는 것이 아닌, 큐에서 데이터를 뽑을 때 방문처리를 하였다.

최소시간이 갱신됨에 따라 현재 노드의 시간이 최소시간보다 클 경우 리턴해주었다. 조건을 걸어줌에도 불구하고 현재 위치가 조건으로 하였던 십만보다 커진다. 이부분에 대해서는 친구들과 이야기를 나누어봐야겠다. ^_^