
문제
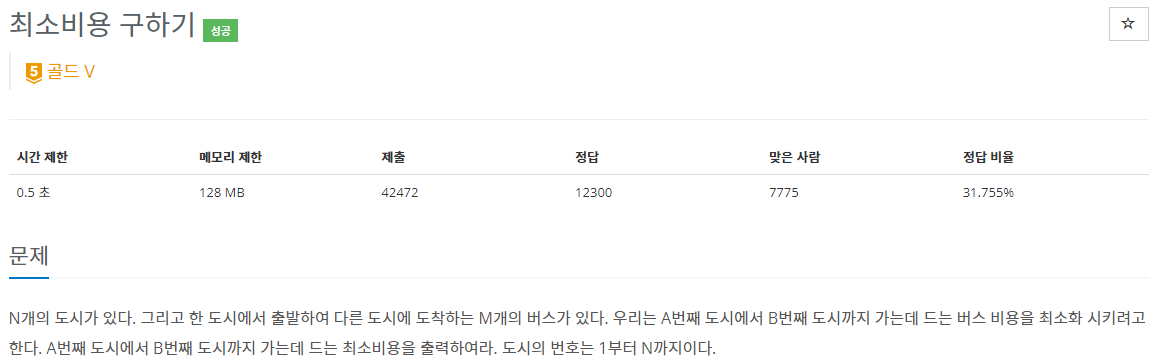
입력 및 출력
풀이
import java.io.*;
import java.util.*;
class Main {
public static int N, M; // N개의 도시, M개의 버스
public static int start, arrive; // 시작 도시, 도착 도시
public static int[] dist; // 최단 거리를 저장하는 배열
public static ArrayList < Node > [] Node; // 버스 정보 확인
public static void main(String args[]) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// N개의 도시, M개의 버스
N = Integer.parseInt(br.readLine());
M = Integer.parseInt(br.readLine());
// 1부터 시작하기 때문에 N + 1만큼 배열 공간 할당
dist = new int[N + 1];
// 최단 거리를 저장하는 배열에 가장 큰 값 저장
Arrays.fill(dist, Integer.MAX_VALUE);
// 노드 초기화
Node = new ArrayList[N + 1];
for (int i = 1; i <= N; i++) {
Node[i] = new ArrayList < > ();
}
for (int i = 0; i < M; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
// 노드의 출발 지점 인덱스에 새로운 노드 객체를 저장(도착 지점, 가중치)
Node[from].add(new Node(to, weight));
}
// 출발 지점, 도착지점을 각 변수에 저장
StringTokenizer st = new StringTokenizer(br.readLine());
start = Integer.parseInt(st.nextToken());
arrive = Integer.parseInt(st.nextToken());
// 다익스트라 함수 호출
System.out.println(dijkstra(start));
}
private static int dijkstra(int start) {
// 다익스트라 알고리즘을 풀기 위한 우선순위 큐
PriorityQueue < Node > pq = new PriorityQueue < > ();
// 우선순위 큐에 출발지와 0을 넣은 객체 노드를 넣는다.
pq.offer(new Node(start, 0));
// 출발지에 거리는 자기 자신의 위치이므로 0을 넣는다.
dist[start] = 0;
// 큐가 비어있지 않을 경우
while (!pq.isEmpty()) {
// 큐의 가장 앞에 있는 값을 반환
Node node = pq.poll();
// dist[도시]값이 가중치를 넣을 당시 경로보다 더 작은 경우
if (dist[node.end] < node.weight) {
continue;
}
// 노드의 각 인덱스는 리스트로 되어있므로 그 사이즈만큼 반복수행
for (int i = 0; i < Node[node.end].size(); i++) {
Node temp = Node[node.end].get(i);
// dist[temp.end]의 값이 dist[node.end] + temp.weight값보다 클 경우
if (dist[temp.end] > dist[node.end] + temp.weight) {
dist[temp.end] = dist[node.end] + temp.weight;
pq.add(new Node(temp.end, temp.weight));
}
}
}
// 결과 값 리턴
return dist[arrive];
}
}
class Node implements Comparable < Node > {
int end, weight;
public Node(int end, int weight) {
this.end = end;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
return Integer.compare(this.weight, o.weight);
}
}결과 및 해결방법
[결과]

[정리]
우선순위 큐
일반적으로 큐는 스택과 다르게 FIFO(First In First Out)의 구조를 갖는다. 우선순위큐는 먼저 들어온 순서대로 데이터가 나가는 것이 아닌 우선순위를 먼저 결정하고 그 우선순위가 높은 엘리먼트가 먼저 나가는 자료구조이다.
우선순위큐는 힙을 이용하는 것이 일반적이고, 데이터를 삽입할 때 우선순위를 기준으로 최대 힙 또는 최소 힙을 구성하고 데이터를 꺼낼 때 루트 노드를 얻어낸 뒤 루트 노드를 삭제할 때는 빈 루트 노드 위치에 맨 마지막 노드를 삽입한 후 아래로 내려가면서 적절한 자리를 찾아서 옮기는 방식으로 진행된다.
[특징]
1. 높은 우선순위 요소를 먼저 꺼내서 처리하는 구조
2. 내부 요소는 힙으로 구성되어 이진트리 구조로 이루어져있다.
3. 내부 구조가 힙으로 구성되어 있기 때문에 시간 복잡도는 O(NLogN)
4. 응급실과 같이 우선순위를 중시해야하는 상황에 쓰인다.
참고 페이지: https://coding-factory.tistory.com/603
해결방법
배우면 배울수록 알쏭달쏭한게 더 많아지는 것 같다.
ArrayList나 배열은 단독으로 사용한 적은 있어도, 위와 같이 함께 사용한 적은 처음이였고 이러한 표기 방식도 생소했던 것 같다. ArrayList타입을 갖는 배열을 만듦으로써, 인접행렬을 표현할 수 있게 되었다.
참고 페이지: https://sarah950716.tistory.com/12
M만큼 반복문을 수행하며 Node배열의 from인덱스에 새로운 노드 객체를 추가하였다. 이때 노드객체는 도착지와 가중치의 값을 갖는다.
가장 중요한 다익스트라 함수를 구현하기 위해 우선순위 큐를 선언하였다. 우선순위 큐는 위의 설명과 같은 특징을 갖는다. 추선순위 큐에 출발지와 0을 넣은 객체 노드를 넣는다. dist배열은 최단거리 정보를 저장하는 배열로서 처음 위치는 자기 자신의 위치이므로 0을 넣는다.
다음으로 BFS함수와 비슷하게 구현된다. 우선순위의 큐가 비어있지 않을 경우 가장 앞의 원소를 꺼내고 해당 정보를 Node변수에 저장한다. 기존의 최소거리보다 현재의 가중치가 큰 경우 다음 반복문을 수행한다. 그 외의 경우라면, 현재 인덱스와 연결된 모든 지점을 확인하며 최단거리를 갱신한다.
결과적으로 dist배열에는 최단거리만 남을 것이고, 도착지점에 대한 결과값을 리턴한다.