[JAVA/1929번] 소수 구하기

---

문제

---

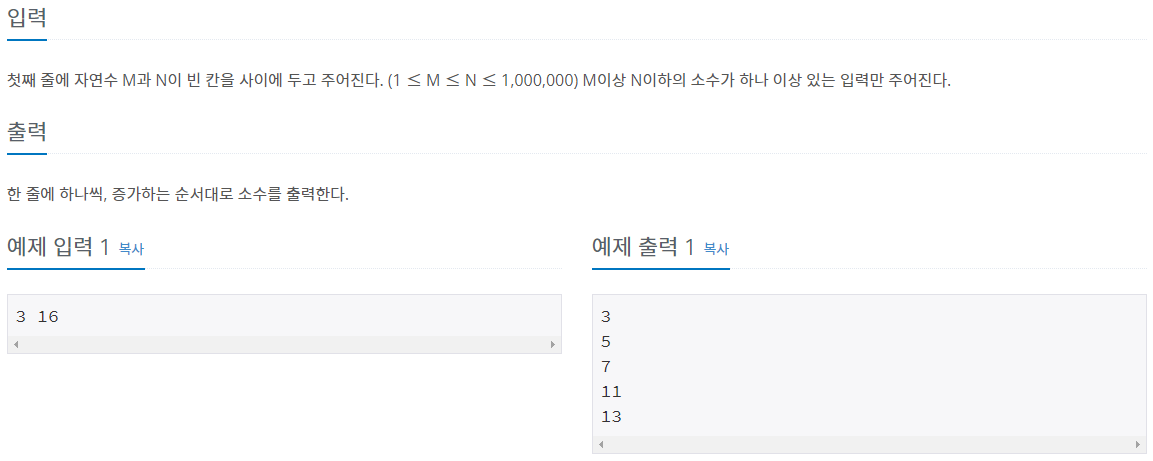
입력 및 출력

---

풀이

import java.io.*;
import java.util.*;

class Main {
    // 소수를 판별하기 위한 메서드
    public static boolean PrimeNumber(int number) {
        // number가 1인경우 소수가 아니기 때문에 false
        if (number < 2) {
            return false;
        }

        // 2부터 i의 제곱이 넘어온 number변수보다 작을 경우 반복문을 수행
        for (int i = 2; i * i <= number; i++) {
            // 나머지가 0일 경우 소수가 아니므로 false
            if (number % i == 0) {
                return false;
            }
        }

        // 그 외의 경우 number는 소수이기 때문에 true 
        return true;
    }

    public static void main(String args[]) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        // 사용자로부터 숫자 두 개를 입력받고 M과 N에 변환을 한 후 대입
        String[] strArray = br.readLine().split(" ");

        int M = Integer.parseInt(strArray[0]);
        int N = Integer.parseInt(strArray[1]);

        // M부터 N까지 반복문 수행
        for (int i = M; i <= N; i++) {
            // true일 경우, 소수이기 때문에 출력
            if (PrimeNumber(i) == true) {
                System.out.println(i);
            }
        }
    }
}

---

결과 및 해결방법

[결과]

[정리]

소수(Prime Number)
소수는 자신보다 작은 두 개의 자연수를 곱하여 만들 수 없는 1보다 큰 자연수이다.
예를들어, 3은 3*1 또는 1*3으로 곱한 결과를 적는 유일한 방법이 자신을 포함하기 때문에 3은 소수이다.

해결방법
소수를 판별하기위한 방법 중 가장 기초가 되는 방법은, 2부터 파라미터로 넘어온 값까지 반복문을 수행하며 0으로 나누어 떨어지지 않는 수가 소수임을 착안해서 문제를 해결하였다.

[기본적인 방법]
가장 기본적인 방법을 사용하면 아래와 같이 구현할 수 있다.

public static boolean PrimeNumber(int number) {
    // number가 1인경우 소수가 아니기 때문에 false
    if (number < 2) {
        return false;
    }

    // 2부터 i의 제곱이 넘어온 number변수보다 작을 경우 반복문을 수행
    for(int i = 2; i < number; i++) {
    	if(num % i == 0){
        	return false;
        }
    }
    // 그 외의 경우 number는 소수이기 때문에 true 
    return true;
}

2부터 파라미터로 넘어 온 number까지 나누어보고, 나머지가 0이 안나온다면 소수로 정의한다. 위 방식은 파라미터로 넘어 온 숫자까지 반복문을 수행하기 때문에 O(N)의 시간복잡도를 갖는다.

[시간을 줄이는 방법]
√number까지 확인하는 방법으로, 원리는 약수의 중심을 구하는 방법이다.
예를 들어 20의 약수는 (1, 2, 4, 5, 10, 20)으로 구성되어 있다. 20을 만들기 위한 쌍을 구분할 수 있는데, [1, 20], [2, 10], [4, 5]로 구분을 지을 수 있다.

√20의 값은 대략 4.xxx의 값임을 알 수 있다. 이를 통해 루트를 씌운 값이 곧 중간값임을 파악할 수 있다.

이 원리를 이용하여, 2부터 √number까지 반복문을 수행한다면 이후의 값은 확인할 필요가 없게되고 O(√N)의 시간 복잡도를 갖게 될 것이다. 아래의 코드는 루트 함수를 이용하지않고, i의 제곱값으로 표기하여 문제를 해결하였다.

public static boolean PrimeNumber(int number) {
    // number가 1인경우 소수가 아니기 때문에 false
    if (number < 2) {
        return false;
    }

    // 2부터 i의 제곱이 넘어온 number변수보다 작을 경우 반복문을 수행
    for (int i = 2; i * i <= number; i++) {
        // 나머지가 0일 경우 소수가 아니므로 false
        if (number % i == 0) {
            return false;
        }
    }

    // 그 외의 경우 number는 소수이기 때문에 true 
    return true;
}