Floating Point

예시

-118.625

1. 먼저 음수이므로 최상위 비트를 1로 설정합니다. (양수일 경우 0)

2. 절댓값 118.625를 이진법으로 변환합니다.
   118.625 -> 1110 110.101

3. 소수점을 왼쪽으로 이동시켜 정수부가 한자리가 되도록 합니다.
   1110 110.101 -> 1.1101 1010 1

4. 3번에서 이동시킨 자릿수(6)만큼을 2의 지수로 사용하여 곱해주고, 이 수를 정규화된 부동 소수점이라고 합니다.
   1.1101 1010 1 x 2^6

5. 4번의 소수점 아래 부분(1101 1010 1)이 가수부(23bit)가 되도록 나머지 비트를 0으로 채웁니다.
   1101 1010 1000 0000 0000 000 x 2^6

6. 위 23비트를 가수부로 설정합니다.

7. 32bit IEEE 754 형식엔 "Bias" 라는 고정된 값이 있습니다. 이는 127이며, bias를 2의 지수인 6에 더하고 이진수로 변환합니다.
   6 + 127 = 133 -> 1000 0101 (8bit 지수부)

8. 위 8비트를 지수부로 설정합니다.

Floating Point 에러

컴퓨터는 부동소수점(floating-point) 숫자를 정확하게 표현할 수 없을 때가 있어, 더하기나 빼기 같은 연산 결과가 우리가 기대한 것과 미세하게 다를 수 있습니다.

이유:
2진법 표현의 한계:
대부분의 실수(예: 0.1, 0.2)는 2진법으로 정확히 표현할 수 없습니다.

예를 들어, 0.1은 2진법으로 무한히 반복되는 값(0.000110011...)이 되어 근사값으로 저장됩니다.
근사값 연산:
이런 근사값들로 계산하다 보니 결과에 오차가 생깁니다.

예: 0.1 + 0.2는 우리가 기대하는 0.3 대신 0.30000000000000004가 나올 수 있습니다.

파이썬에서 부동소수점 덧셈 오류를 잘 보여주는 간단한 예시를 살펴보겠습니다. 부동소수점 연산은 항상 정확한 결과를 보장하지 않기 때문에, 덧셈 연산 후 기대한 값과 실제 값이 약간 다를 수 있습니다.

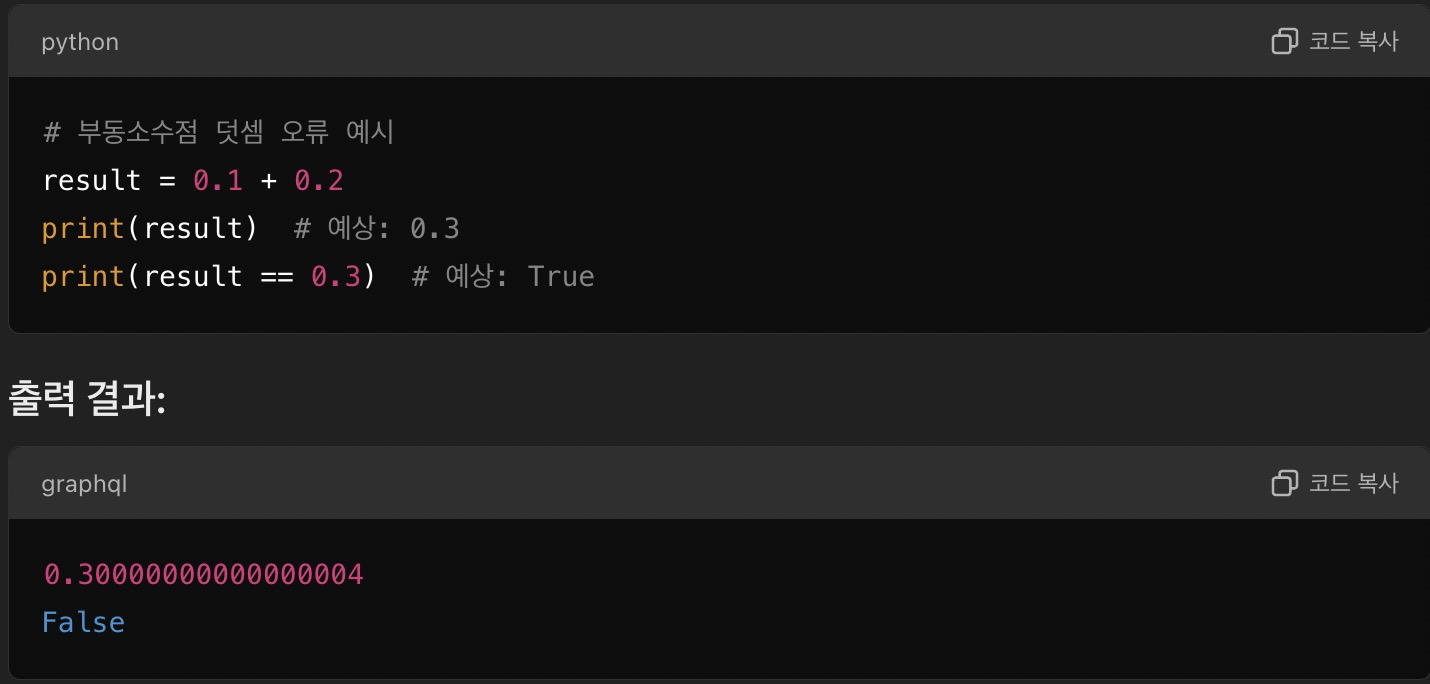
뭐 이런 식으로 해결할 수 있다.