시간 복잡도 (time complexity)
정의
- 입력값과 문제를 해결하는데 걸리는
시간의 상관관계 - 입력값이 늘어나도
시간이 덜 늘어나는알고리즘이 좋은 알고리즘 - 각 줄이 실행되는 것을
한 번의 연산으로 생각
예시 1
- 아래의 코드를 예시로 시간 복잡도를 구해보자.
def find_max_num(array):
for num in array: # array 의 길이만큼 아래 연산이 실행
for compare_num in array: # array 의 길이만큼 아래 연산이 실행
if num < compare_num: # 비교 연산 1번 실행
break
else:
return num
input = [3, 5, 6, 1, 2, 4]
result = find_max_num(input)- 위의 함수는 각 숫자마다
모든 다른 숫자와 비교해서 최대값인지 확인하고 있다. 만약 다른 모든 값보다크다면 반복문을 중단하도록 짜여있다. - 위 함수의 시간 복잡도를 계산해보자.
- 현재 함수는 input 값으로 들어온 배열을 활용하고 있다.
- 또한 이중 for 문을 사용해
num을 array에 있는 다른compare_num과모두 비교하고 있다. - 배열의 길이는 n이므로 한 번의 for 문을 실행할 때 걸리는 시간은
N이다. 비교 연산의 경우,1만큼의 시간이 걸리게 된다. - 따라서 for 문을 2 번 돌리면서 비교연산을 하는데 걸리는 시간은
N × N × 1 = 𝑶(𝑵²)으로 계산할 수 있다.
예시 2
def find_max_num(array):
max_num = array[0] # 연산 1번 실행
for num in array: # array의 길이만큼 아래 연산이 실행
if num > max_num: # 비교 연산 1번 실행
max_num = num # 대입 연산 1번 실행
return max_num
input = [3, 5, 6, 1, 2, 4]
result = find_max_num(input)- 위의 코드는 아래와 같이 아래와 같은 연산이 필요하다.
- max_num 대입 연산 1번
- array의 길이 X (비교 연산 1번 + 대입 연산 1번)
- 이를 수식으로 표현하면
1 + 2 × 𝑵이므로2𝑵 + 1로 표현할 수 있지만, 시간 복잡도가 입력값에 따라 계속 커지게 되면 상수들은 큰 의미가 없게 된다. - 따라서 시간 복잡도는
𝑶(𝑵)이다.
비교
-
위에서 비교한 두 예시의 시간 복잡도를 입력값을 늘려감에 따라 어떻게 변하는지 비교해보도록 하겠다.
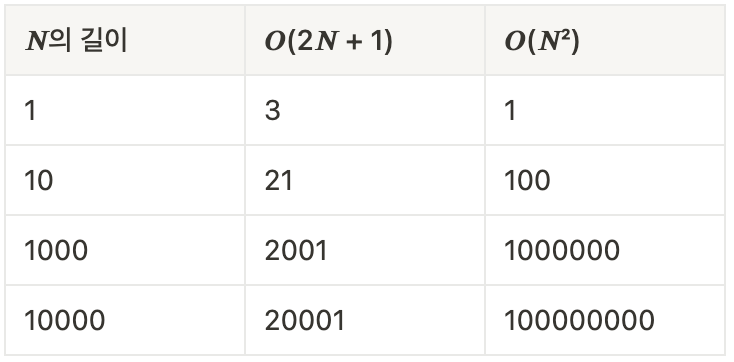
-
예시 2에서 상수값들은 큰 의미가 없다고 이야기하면서 전부 제거했었다. 위의 표를 보면 상수값은 시간 복잡도 비교에 별다른 영향을 주지 않는 것을 볼 수 있다.
-
따라서 상수값들을 제거한 값들로 다시 비교해보도록 하겠다.
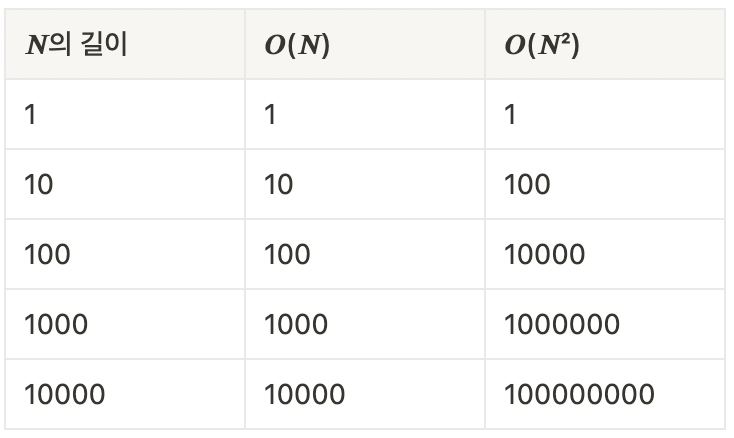
-
입력값에 따라 시간 복잡도가 복잡할 수록 소요되는 시간이 엄청나게 커지는 것을 볼 수 있다. 이 표를 보면서 무심코 이중 for 문을 사용했던 것을 돌이켜 보게 되는 것 같다.
- 만약 상수의 연산량이 필요하다면, 만큼의 연산량이 필요하다고 말하면 된다.
공간 복잡도 (space complexity)
정의
- 입력값과 문제를 해결하는 데 걸리는
공간과의 상관관계 - 입력값이 늘어나도 걸리는
공간이 덜 늘어나는 알고리즘이 좋은 알고리즘
예시 1
def find_max_occurred_alphabet(string):
# 26개의 공간
alphabet_array = ["a", "b", "c", "d", "e", "f", "g", "h", "i", "j", "k", "l", "m", "n", "o", "p", "q", "r", "s", "t", "u", "v", "x", "y", "z"]
max_occurrence = 0 # 1개의 공간
max_alphabet = alphabet_array[0] # 1개의 공간
for alphabet in alphabet_array:
occurrence = 0 # 1개의 공간
for char in string:
if char == alphabet:
occurrence += 1
if occurrence > max_occurrence:
max_alphabet = alphabet
max_occurrence = occurrence
return max_alphabet
result = find_max_occurred_alphabet-
위의 함수가 사용하는 공간은
26 + 1 + 1 + 1이므로 공간 복잡도는29이다. -
시간 복잡도
for alphabet in alphabet_array: # alphabet_array 의 길이(26)만큼 아래 연산이 실행 occurrence = 0 # 대입 연산 1번 실행 for char in string: # string 의 길이만큼 아래 연산이 실행 if char == alphabet: # 비교 연산 1번 실행 occurrence += 1 # 대입 연산 1번 실행 if occurrence > max_occurrence: # 비교 연산 1번 실행 max_alphabet = alphabet # 대입 연산 1번 실행 max_occurrence = number # 대입 연산 1번 실행- alphabet_array 의 길이 × 대입 연산 1번
- alphabet_array 의 길이 × string의 길이 × (비교 연산 1번 + 대입 연산 1번)
- alphabet_array 의 길이 × (비교 연산 1번 + 대입 연산 2번)
- string 의 길이는 보통
𝑵으로 표현한다. - 따라서
26 × (1 + 2×𝑵 + 3) = 52𝑵 + 104이므로 시간 복잡도는𝑶(𝑵)이다.
예시 2
def find_max_occurred_alphabet(string):
alphabet_occurrence_list = [0] * 26 # 26개의 공간
for char in string:
if not char.isalpha():
continue
arr_index = ord(char) - ord('a') # 1개의 공간
alphabet_occurrence_list[arr_index] += 1
max_occurrence = 0 # 1개의 공간
max_alphabet_index = 0 # 1개의 공간
for index in range(len(alphabet_occurrence_list)):
alphabet_occurrence = alphabet_occurrence_list[index] # 1개의 공간
if alphabet_occurrence > max_occurrence:
max_occurrence = alphabet_occurrence
max_alphabet_index = index
return chr(max_alphabet_index + ord('a'))
result = find_max_occurred_alphabet-
위의 함수가 사용하는 공간은
26 + 1 + 1 + 1 + 1이므로 공간 복잡도는30이다. -
시간 복잡도
for char in string: # string 의 길이만큼 아래 연산이 실행 if not char.isalpha(): # 비교 연산 1번 실행 continue arr_index = ord(char) - ord('a') # 대입 연산 1번 실행 alphabet_occurrence_list[arr_index] += 1 # 대입 연산 1번 실행 max_occurrence = 0 # 대입 연산 1번 실행 max_alphabet_index = 0 # 대입 연산 1번 실행 for index in range(len(alphabet_occurrence_list)): # alphabet_array 의 길이(26)만큼 아래 연산이 실행 alphabet_occurrence = alphabet_occurrence_list[index] # 대입 연산 1번 실행 if alphabet_occurrence > max_occurrence: # 비교 연산 1번 실행 max_occurrence = alphabet_occurrence # 대입 연산 1번 실행 max_alphabet_index = index # 대입 연산 1번 실행- string의 길이 X (비교 연산 1번 + 대입 연산 2번)
- 대입 연산 2번
- alphabet_array 의 길이 X (비교 연산 1번 + 대입 연산 3번)
𝑵 × (1 + 2) + 2 + 26 × (1 + 3) = 3𝑵 + 106이므로3𝑵 + 106만큼의 시간이 걸리고, 시간 복잡도는 상수를 모두 버리게 되므로𝑶(𝑵)이다.
비교
- 위의 두 예시의 공간 복잡도는 29 와 30이다.
- 즉, 공간의 차이도 별로 나지 않을 뿐더러
상수이기 때문에 크게 신경쓸 것이 없다. - 이처럼
대부분의 문제에서는 알고리즘의 성능이 공간에 의해서 결정되지 않는다. - 따라서 위에서 구했던 시간 복잡도를 비교해보자.
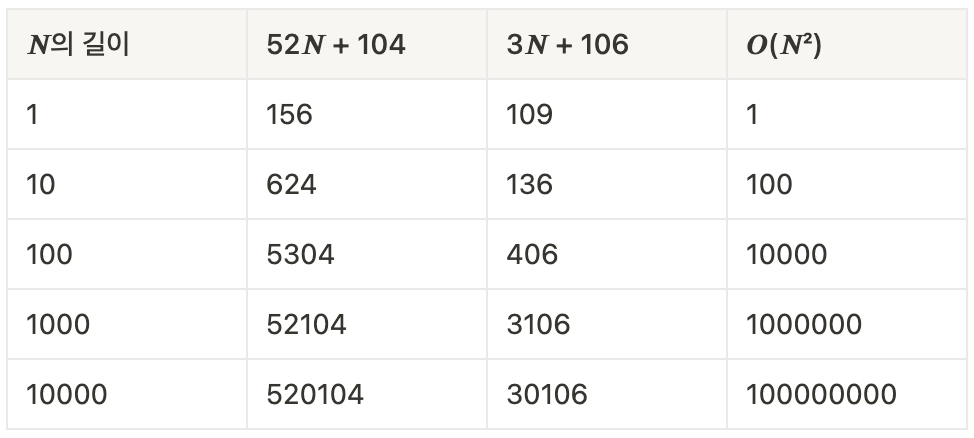
- 두 예시는 둘 다 시간 복잡도가
𝑶(𝑵)이므로 비교할 것이 없으므로, 상수값도 전부 붙여𝑶(𝑵²)과 얼마나 차이가 나는지 확인해보도록 하겠다.