알고리즘 문제
알고리즘
: 문제 해결 최선의 선택
: 문제를 이해하고 어떻게 풀 것인지 전략을 세우는 것
-> 자료구조, 알고리즘
-> 특정 방법을 이용해 풀어보라는 의도가 있는 문제가 많이 나온다 [수학적 사고, 컴퓨팅 사고]
풀이 단계
1)어떤 개념을 요구하는지 파악
2)개념에 맞는 해결 방법 분석
주요 수학적 개념
- GCD/LCM (최대공약수, 최소공배수)
- 순열/조합
- 멱집합
1.순열과 조합
문제 : 카드 뽑기
5장 중 3장 선택+나열
1. 순서 생각 : 1장씩 나열하면서 나열된 카드가 3장에 도달하면 나열 중지
- 첫번째 카드 선택 방법 : 5가지
- 두번째 카드 선택 방법 : 4가지
- 세번째 카드 선택 방법 : 3가지
순열 : n개 중에서 일부만을 선택하여 나열하는 것
->순서가 다르면 다른 경우로 파악한다
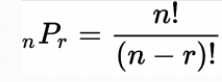

2. 순서 생각X
5장에서 3장 선택할 때 하나의 그룹으로 선택
- 순열로 구할 수 있는 경우 찾기
- 순열로 구할 수 있는 경우에서 중복된 경우의 수를 나눈다
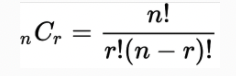
5장에서 3장을 무작위로 선택하는 조합에서 모든 경우의 수
문제 : 소수 찾기
한 자리 숫자가 적힌 종잇조각이 흩어져 있다
흩어진 종잇조각을 붙여 소수 몇 개
종잇조각으로 만들 수 있는 소수 몇 개
- n개의 숫자 중에 1~k개를 뽑아서 순열 생성
- 각 순열을 정수로 변환하고 해당 정수가 중복되지 않으면서 동시에 소수인지 검사
- 소수이면 개수를 센다
순서에 의해 전혀 다른 값이 될 수 있다
123 321은 전혀 다른 숫자니까
문제 : 일곱 난장이
9명의 난쟁이 중 진짜 7명을 가려내야 한다
7명의 합은 100
9명 각각의 키가 주어질 때 원래 7명을 찾는 방법은?
난쟁이의 순서를 생각하지 않고 키를 합했을 때 100이 되는 경우를 찾는다 =조합
순열과 조합을 활용하는 문제는 문제를 먼저 이해하고 지문 속에서 힌트를 얻어 활용
2.GCD/LCM
약수 : 어떤 수를 나누어떨어지게 하는 수
배수 : 어떤 수의 1,2,3,...n배하여 얻는 수
공약수 : 둘 이상의 수의 공통인 약수
공배수 : 둘 이상의 수의 공통인 배수
최대 공약수(GCD) : 둘 이상의 공약수 중에서 최대인 수
최소 공배수 : 둘 이상의 공배수 중에서 최소인 수
3. 멱집합
어떤 집합이 있을 때, 이 집합의 모든 부분집합을 멱집합
모든 부분집합을 나열하는 방법
: 가장 앞 원소(임의의 집합 원소)가 있는지, 없는지에 따라 단계 나눔
Step A: 1을 제외한 {2, 3}의 부분집합을 나열합니다.
Step B: 2를 제외한 {3}의 부분집합을 나열합니다.
Step C: 3을 제외한 {}의 부분집합을 나열합니다. → {}
Step C: {}의 모든 부분집합에 {3}을 추가한 집합들을 나열합니다. → {3}
Step B: {3}의 모든 부분집합에 {2}를 추가한 집합들을 나열합니다.
Step C: {3}의 모든 부분집합에 {2}를 추가한 집합들을 나열하려면,
{}의 모든 부분집합에 {2}를 추가한 집합들을 나열한 다음
{}의 모든 부분집합에 {2, 3}을 추가한 집합들을 나열합니다. → {2}, {2, 3}
Step A: {2, 3}의 모든 부분집합에 {1}을 추가한 집합들을 나열합니다.
Step B: {2, 3}의 모든 부분집합에 {1}을 추가한 집합들을 나열하려면,
{3}의 모든 부분집합에 {1}을 추가한 집합들을 나열한 다음
{3}의 모든 부분집합에 {1, 2}를 추가한 집합들을 나열합니다.
Step C: {3}의 모든 부분집합에 {1}을 추가한 집합을 나열하려면,
{}의 모든 부분집합에 {1}을 추가한 집합들을 나열한 다음
{}의 모든 부분집합에 {1, 3}을 추가한 집합들을 나열합니다. → {1}, {1, 3}
Step C: {3}의 모든 부분집합에 {1, 2}를 추가한 집합을 나열하려면,
{}의 모든 부분집합에 {1, 2}를 추가한 집합들을 나열한 다음 {}의 모든 부분집합에
{1, 2, 3}을 추가한 집합들을 나열합니다. → {1, 2}, {1, 2, 3}
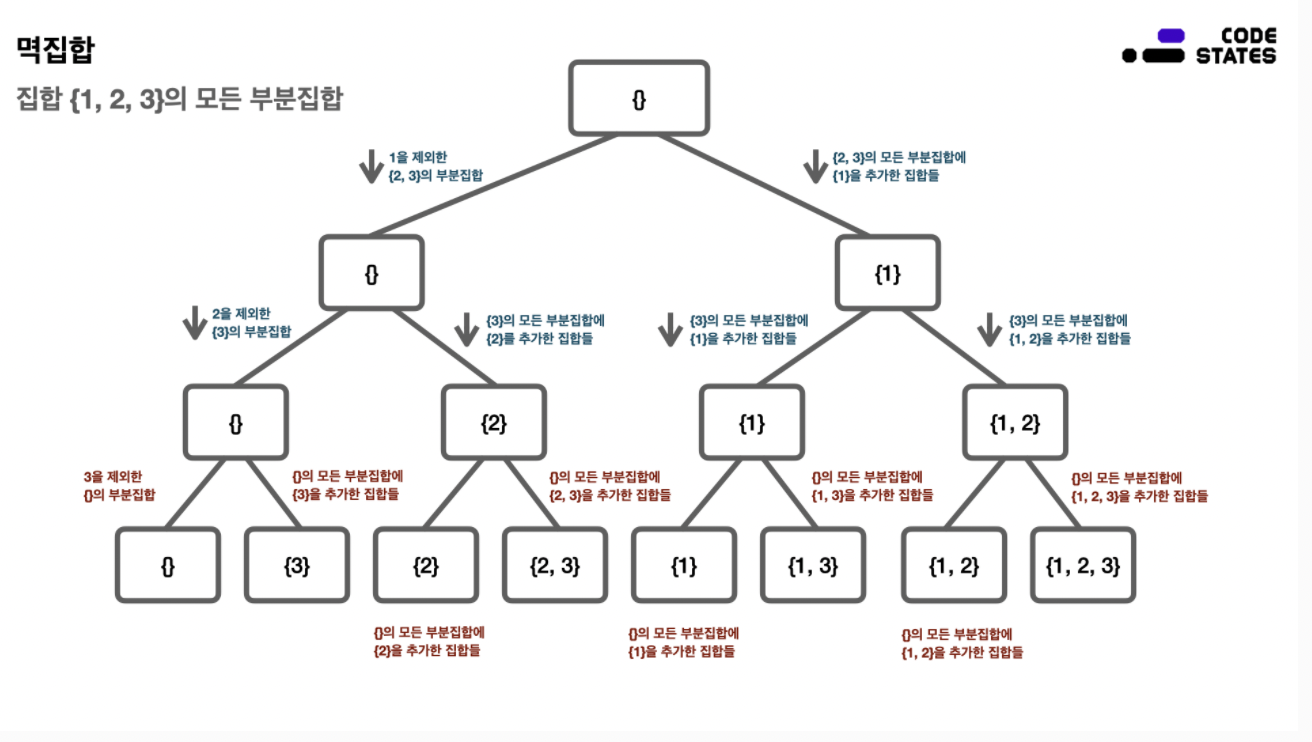
트리 문제는 아님. 그냥 이해 위해
순환구조를 띤다
-> 임의의 원소를 제외하면서 집합을 작은 단위로 줄여나가는 방법
작은 단위로 줄여나가는 재귀를 응용할 수 있다
PowerSet이라는 멱집합의 개수 리턴하는 함수
자기 자신 호출, 더 작은 문제로 문제의 크기 줄여 해결
가장 작은 단위로 줄어들고 함수가 리턴될 때 카운트를 올리는 방식으로