c++/ 자료구조&알고리즘 개념 복습하기 - 21 / 세그먼트 트리

< 세그먼트 트리>

• 각 노드는 특정 구간을 대표하다

• 이진 트리 구조 (완전)

• 부모 노드가 대표하는 구간은 자식 노드 두 개가 대표하는 구간의 합집합이다

• 부모 노드가 담당하는 구간을 반씩 나누어 왼쪽 자식, 오른쪽 자식 탐색

• 구간의 길이가 1이라면 리프노드! (구간 시작 번호와 마지막 번호가 같다) -> 입력으로 주어진 배열에서 시작 번호의 순서에 해당하는 원소의 값을 할당해주면 된다
  
  

• 값 변경 시 갱신 쿼리 : 이 값을 포함하는 O(logN)개의 노드에 대해 갱신

• 구간 합 쿼리 : 구간을 표현하는 O(longN)개의 노드들을 탐색 후 총합 구하기

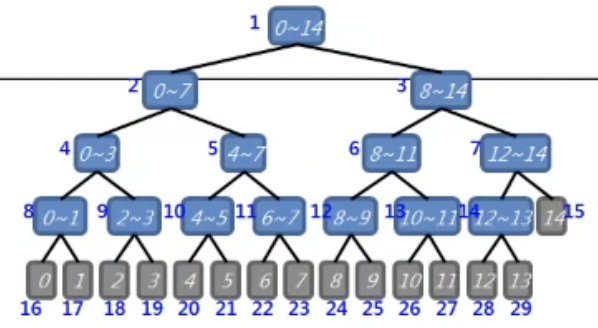
(이미지 출처 : https://www.youtube.com/watch?v=ahFB9eCnI6c)

• 위 사진에서 1번 노드는 배열의 0~14 인덱스 즉, 전체 구간의 합을 나타낸다

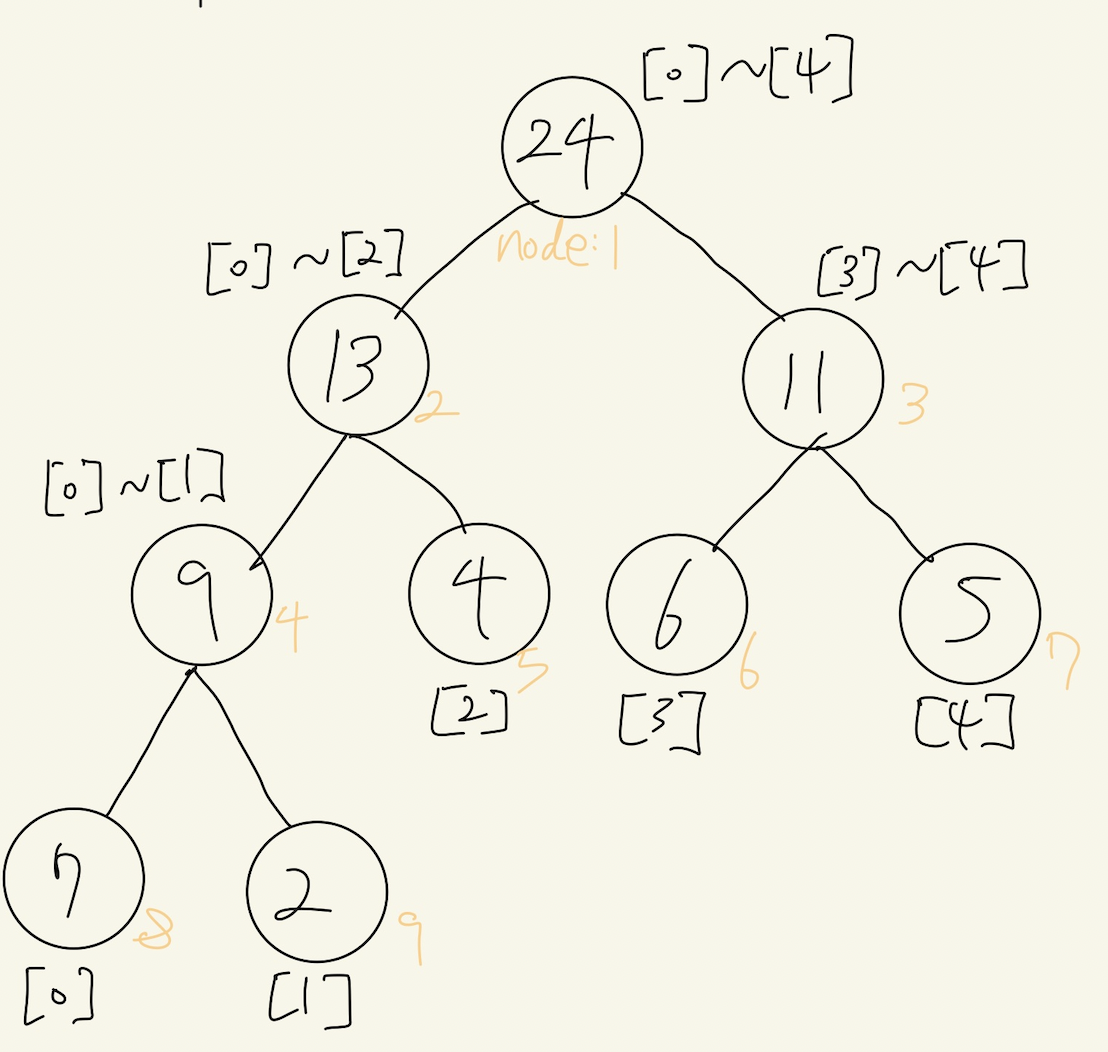
< 세그먼트 트리 채우기 >

int arr[5] = {7, 2, 4, 6, 5};
int segmentTree[20] = {0};

int init(int start, int end, int node) {
    if(start == end) { // 리프노드 도달, 담당하는 구간의 길이 = 1
        segmentTree[node] = arr[start];
        return segmentTree[node];
    }
    int mid = (start + end) / 2; 
    // start + end 에서 long 범위가 넘어가는 경우도 있으니 문제 조건 잘 확인하기!
    // 세그먼트 트리문제에서는 사실 int 범위를 넘어가는 경우는 거의 없겠지만 알아두기, 이분탐색 대비
    
    segmentTree[node] = init(start, mid, node * 2) + init(mid + 1, end, node * 2 + 1);
    // start ~ end를 반복적으로 반씩 나눈다 -> 부모노드가 담당하는 구간을 반으로 나누는 것

    return segmentTree[node];
}


int main()
{
    int sum = init(0, 3, 1);
    // 자식 노드 계산을 위해 노드 번호 시작은 1부터 !!
    cout << sum << "\n";

    return 0;
}

< 특정 구간의 합 구하기 >

// start ~ end = 현재 검사 대상인 구간
// left ~ right = 답을 위해 탐색할 구간
int sum(int start, int end, int node, int left, int right) { 
    if(start > right || end < left) return 0; // 찾으려는 구간 외 범위
    if(start >= left && end <= right) return segmentTree[node];
    // 현재 구간이 구하려는 구간에 포함된다

    int mid = (start + end) / 2;
    return sum(start, mid, node * 2, left, right) 
        + sum(mid + 1, end, node * 2 + 1, left, right);
}

< 특정 인덱스 갱신하기 >

• 입력 배열에서 특정 인덱스를 갱신 -> 이 인덱스가 포함된 모든 구간의 합을 갱신
• 기존 값에서 새로 변경할 값의 차를 구해서 각 구간에 더해주는 방식

// value : 기존의 값 - 새로 할당할 값 -> 업데이트 대상 노드가 포함된 구간 합에 value 값을 더해주면 된다
// index : 입력 배열에서 변경시킬 값의 index
void update(int start, int end, int node, int index, int value) {
    if(start > index || end < index) return;
    // 현재 구간에 변경시킬 index 포함되지 않음

    segmentTree[node] += value; // 구간합 갱신, 리프노드라면 해당 인덱스 값 갱신
    if(start == end) return; // 리프노드 도달

    int mid = (start + end) / 2;
    update(start, mid, node * 2, index, value);
    update(mid + 1, end, node * 2 + 1, index, value);
}

---

• < 참고 링크 >
• https://yeonyeon.tistory.com/155