<연결 리스트>
- 원소들을 저장할 때 그 다음 원소가 있는 위치를 포함하는 방식의 자료구조
< 연결 리스트 성질 >
-
k번째 원소를 확인/변경하기 위해 O(k)가 필요하다
-
배열과 다르게 O(1) 접근이 불가
-
임의의 위치에 원소를 추가/삭제 = O(1)
-
원소들이 메모리 상에 연속해있지 않아 Cache hit rate가 낮지만 할당이 다소 쉽다
< 연결 리스트 종류 >
- 단일 연결 리스트 : 다음 원소의 주소 포함
- 이중 연결 리스트 : 이전 원소, 다음 원소의 주소 포함 -> 단, 원소가 가지고 있는 정보가 1개 늘어났기 때문에 메모리를 더 사용한다
- 원형 연결 리스트 : 마지막 원소와 첫 원소가 연결
< 배열 vs 연결리스트 >
| 배열 | 연결리스트 | |
|---|---|---|
| k번째 원소 접근 | O(1) | O(k) |
| 임의 위치 원소 추가/제거 | O(N) | O(1) |
| 메모리 상의 배치 | 연속 | 불연속 |
| 추가적으로 필요한 공간(Overhead) | - | O(N) |
-
연결리스트에서 임의 위치 원소에서 추가/제거 를 하는 것은 O(1) 이지만 해당 위치까지 이동을 처음부터 해야하므로 결국 O(N) + O(1) -> O(N)이 된다
-
배열은 추가적으로 필요한 공간이 없다, 굳이 필요하면 배열의 길이 정보를 저장할 int 변수 1개 정도가 있다
-
연결리스트는 이전, 다음 원소의 주소값을 가지고 있어야 한다
-> ex> 64비트 컴퓨터라면 주소값이64비트(8바이트) 단위이므로 8N 바이트가 추가로 필요하게 된다
-> N에 비례하는 만큼의 메모리를 추가로 사용하게 된다
<연결리스트 구현>
struct NODE{
struct NODE *prev, *next;
int data;
}연결리스트의 구현은 위와 같이 노드 구조체 혹은 클래스를 만들어서 원소가 생성될 때 동적할당을 하는 방식이다
but 시간이 중요한 코딩테스트에서는 STL list를 사용해보도록 하자
< STL list >
- STL list는 doubly linked list 구조를 가지고 있다!
- 인덱스 접근은 불가
#include <bits/stdc++.h>
using namespace std;
int main(void) {
list<int> L = {1,2}; // 1 2
cout << L.size() << '\n';
list<int>::iterator t = L.begin(); // t는 1을 가리키는 중
L.push_front(10); // 10 1 2
cout << *t << '\n'; // t가 가리키는 값 = 1을 출력
L.push_back(5); // 10 1 2 5
L.insert(t, 6); // t가 가리키는 곳 앞에 6을 삽입, 10 6 1 2 5
t++; // t를 1칸 앞으로 전진, 현재 t가 가리키는 값은 2
t = L.erase(t); // t가 가리키는 값을 제거, 그 다음 원소인 5의 위치를 반환
// 10 6 1 5, t가 가리키는 값은 5
cout << *t << '\n'; // 5
for(auto i : L) cout << i << ' ';
cout << '\n';
// c++ 11 미만이라면 아래와 같이 순회 구현
for(list<int>::iterator it = L.begin(); it != L.end(); it++)
cout << *it << ' ';
}- c++ 11 이상인 경우
list< int >::iterator t = L.begin() 를
auto t = L.begin()로 작성이 가능하다
#include <string>
#include <vector>
#include <list>
#include <iostream>
using namespace std;
int main() {
list<int> l;
list<int>::iterator iter;
iter = l.begin();
l.push_back(1);
l.push_back(2);
l.push_back(3);
l.push_back(2);
for(iter = l.begin(); iter != l.end(); iter++) {
if(*iter == 3)
break;
}
l.erase(iter); // iter은 현재 3 가리키고 있음
for (iter = l.begin(); iter != l.end(); iter++)
{
cout << *iter << "\n";
}
cout << "/////\n";
cout << l.front() << "\n"; // 맨 앞, 뒤 원소
cout << l.back() << "\n";
return 0;
}
// 출력
1
2
2
/////
1
2< 생각해보기 >
- 원형 연결 리스트 내의 임의의 노드 하나가 주어졌을 때 해당 List의 길이를 효율적으로 구하는 방법은?
-> 동일한 노드가 나올 때 까지 계속 다음 노드로 이동한다
공간복잡도 O(1), 시간복잡도 O(N)
시작점을 어딘가에 따로 하나 저장해두고 계속 다음 노드로 이동하면 된다!
-
중간에 만나는 두 연결리스트의 시작점들이 주어졌을 때 만나는 지점을 구하는 방법은?
-> 두 시작점 각각에 대해 끝까지 이동을 시켜 각 길이를 구한다
다시 두 시작점으로 돌아와 긴쪽은 둘의 차이만큼 먼저 이동을 시켜놓은 다음 두 시작점이 만날 때 까지 한 칸씩 이동을 시킨다.
공간복잡도 O(1), 시간복잡도 O(A+B)
-
연결리스트 안에 사이클이 있는지 판단하기
-> Floyd's cycle-finding algorithm
한 칸씩 이동하는 커서, 두 칸씩 이동하는 커서를 동일 시작점에서 이동을 시작하면 사이클이 있는 경우 반드시 두 커서가 만나게된다
사이클이 없는 경우는 두 커서가 만나지 못하고 연결리스트의 끝에 도달한다
위 방식 사용 시 거치는 노드를 모두 저장할 필요가 없다!
공간복잡도 O(1), 시간복잡도 O(N)
< iterator >
list를 사용하며 탐색, 삽입, 삭제 시 iterator를 유용하게 사용할 수 있다
list <int> L;
if (L.begin() == L.end())
printf("equal\n"); // here
else
printf("differ\n");
list<int>::iterator beg = L.begin();
list<int>::iterator en = L.end();
if (beg == en)
printf("beg == en\n"); // here
else
printf("beg != en\n");
L.insert(L.end(), 1);
if (beg == en)
printf("beg == en\n"); // here
else
printf("beg != en\n");
if (en == L.begin())
printf("en == L.begin()\n");
else
printf("en != L.begin()\n"); // here
if (beg == L.begin())
printf("beg == L.begin()\n");
else
printf("beg != L.begin()\n"); // here
if(en == L.end())
printf("en == L.end()\n"); // here
else
printf("en != L.end()\n");
if (beg == L.end())
printf("beg == L.end()\n"); // here
else
printf("beg != L.end()\n");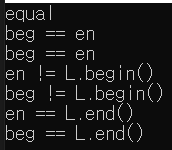
- list에 비어있는 상태에서는 begin과 end가 같은 곳을 가리킨다
- 원소가 하나 추가되면 비어있는 상태에서의 begin과 end가 둘 모두 추가된 상태에서의 end의 값을 가지게 된다

iterator를 활용하여 list.insert, erase를 하는 경우를 그림으로 나타낸 것이다
-
insert의 2번 예제의 경우 iterator가 b를 가리키고 있는 상태이다
-
이때 list.insert(iterator, 'c')를 하면 기존 b의 위치에 c가 삽입이 된다
-
위 iterator는 변하지 않고 b를 가리키는 값이 유지된다!
-
erase의 경우 현재 iterator가 가리키고 있는 위치의 값을 삭제한다
-
erase 2번 예제에서 b를 가리키고 있으므로 b가 삭제가 되며 iterator가 결과적으로 end값이 된다
-
기존에 b 다음에 다른 원소가 있었다면 iterator가 b를 가리키다가 b가 삭제되면서 b 다음에 있던 원소를 가리키게 된다
-
!! 1번 예제에서 처럼 iterator가 현재 end를 가리키고 있는 상태에서 erase를 하면 에러가 발생하므로 주의하자!!!
