<기초 그래프 알고리즘>
- 최단경로 알고리즘
- Strongly Connected Component(그래프 덩어리 몇개?)
- 최소 신장 트리(그래프에서 간선을 제거하여 트리형태로(간선들 합은 최소값을 유지하며))
<최단 경로 알고리즘>

-> A에서 B까지 가는 최단 경로는???
-
다익스트라 알고리즘 : 하나의 정점에서 모든 정점까지의 최단거리를 알 수 있다
-
플로이드 알고리즘 : 모든 정점에서 모든 정점까지의 최단거리를 다 알 수 있다
-
벨만포드 알고리즘 : 하나의 정점에서 모든 정점까지의 최단거리 구한다
벨만포드는 가중치에 음수값 있어도 사용 가능
다익스트라 = 가중치가 모두 양수값이어야 가능
<다익스트라 알고리즘>
-> 정점 X까지 최단거리로 가기 위해서는 그 직전 지점까지도 최단거리로 가야한다!!!

-> x랑 인접한 지점 y1, y2, y3 까지 각각 최단 거리를 구하고
그 다음 x까지의 가중치를 더한 후 각각 비교해서 답을 찾는다
한 점에서 모든 점 까지의 최단거리
= 최단경로 트리
-->> 트리 = 사이클이 없는 그래프
최단경로 트리를 어떻게 만들 것인가?

T(i) = i까지 도달하는 최단거리 (1에서 출발)

1에서 시작하면 우선 1의 간선 중 가중치 낮은 것 먼저 선택
-> 정점6 까지 거리는 1 (출발 정점 1 기준)
-> 정점1 은 자신이 출발점이므로 최단거리 = 0
2까지 최단 거리는 2의 인접한 정점 중 최단거리가 정해진 1,6까지 거리에 각각 2까지의 거리를 더한 것들 중 최소값이다
0 + 3 > 1 + 1 이므로 6에서 오는게 최단거리
-> 정점2까지 최단거리는 1 + 1 = 2
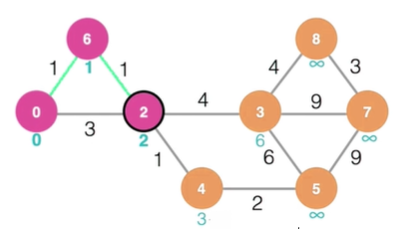
정점 4 기준 인접 정점 중 최단거리가 정해진 정점은 정점2 밖에 없으므로 정점2까지 최단거리에 2-4 가중치를 더한다
-> 정점 4 까지 거리는 2 + 1 = 3 업데이트
정점 3 까지 거리도 2 + 4 = 6으로 우선 업데이트

현재 색칠 안된 것들 중 최소는 3값을 가지는 정점 4이므로 정점 4 확정
정점 4 기준 인접 정점 2를 보면 3 + 1 = 4, 하지만 이미 정점2는 값2를 가지고 있으므로 업데이트x
정점5는 3 + 2 = 5로 업데이트 / 정점5 확정
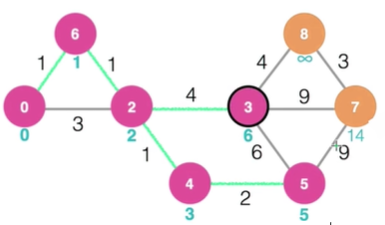
정점5 기준 확정x 중 최소값을 가지는 것은 3
3이 가지고 있던 값6 과 (5까지의 값 + 6)을 비교
6 < 5+ 6
-> 3까지 거리 6으로 확정
나머지 확정x 인 7 까지 거리 우선 5+9 = 14 로 업데이트
이제 정점3이 기준
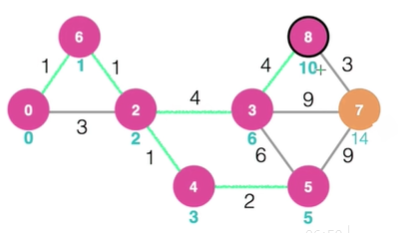
정점3 확정이고
정점 8 -> 6 + 4 = 10으로 업데이트
색칠 안된 것들 중 최소 값을 가지는 8로 이동해서 확정
8에서 7 = 10 + 3과 기존 7 값 14를 비교
정점7 -> 13업데이트
(1) 색칠 x 중 최소값 찾기
(2) 색칠하기
(3) 그 다음 뻗어 나가기
<다익스트라 알고리즘 구현>
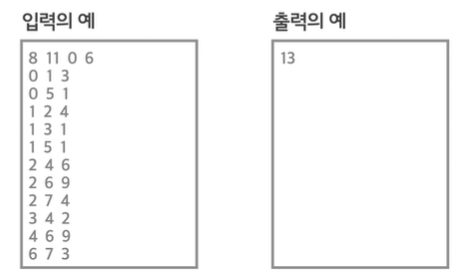
8 = 정점 개수
11 = 간선 개수
0 = 시작점
6 = 끝점
-> 0에서 6까지의 최단 거리를 알고 싶다!
0 1 3 = 0과 1 이 연결되어 있고 그 가중치는 3 이다
#include <stdio.h>
#include <vector>
#include <algorithm>
using namespace std;
// T[i] = 정점 i 에 도달하는데 걸리는 최단 거리
// (1) T[i] 중 최솟값을 정한다. 단, 지금까지 최솟값으로 뽑히지 않았던 값들 중
// (2) 한 index를 최단거리 확정하면 여기서 부터 뻗어나간다
// index 의 인접 정점 들 중 index 를 거쳐가는 게 더 최단이면 그들의 값을 업데이트 한다
const int MAX = 100;
vector<int> graph[MAX]; // 그래프
vector<int> cost[MAX]; // 간선 가중치
int n, m, start, End; // 정점 개수, 간선 개수, 시작점, 끝점
int Table[MAX];
bool Check[MAX]; // true면 해당 정점은 최단거리 확정
// false면 해당 정점은 아직 최단거리 확정되지 않음
int main() {
scanf("%d %d %d %d", &n, &m, &start, &End);
for(int i = 0; i < m; i++){
int a, b, c;
scanf("%d %d %d", &a, &b, &c);
graph[a].push_back(b);
graph[b].push_back(a);
cost[a].push_back(c);
cost[b].push_back(c);
}
//graph[1] : 2 6 8 9 1이 2,6,8,9와 연결
// cost[1] : 1 1 3 9 1에서 2,6,8,9 까지의 가중치가 각각 1 1 3 9
for(int i = 0; i<n; i++) Table[i] = 999999999;
// 테이블 초기에는 매우 큰 값으로 초기화
Table[start] = 0; // 시작점은 자기자신이므로 최단거리 = 0
for(int i = 0; i<n; i++){ // 정점 전체 개수 만큼 반복
// (1) 최솟값을 구한다 / 단, 지금까지 최단거리로 확정되지 않은 정점에 대해서
// (2) 그 최솟값을 갖는 노드로부터 뻗어나간다
int minValue = 999999999;
int minIndex = -1;
for(int j = 0; j<n; j++){
if(!Check[j] && minValue > Table[j]){
// 확정되지 않았으면서
minValue = Table[j];
minIndex = j;
}
}
Check[minIndex] = true; // minIndex 노드는 이제 확정 가능
// 이제 minIndex와 인접한 정점들 값 업데이트 여부 체크
for(int k = 0; k < graph[minIndex].size(); k++ ){
int Node2 = graph[minIndex][k]; // minIndex와 인접한 정점
int Cost2 = cost[minIndex][k];
// minIndex---(cost2)---Node2
if(Table[Node2] > Table[minIndex] + Cost2){
Table[Node2] = Table[minIndex] + Cost2;
} // minIndex를 거치는게 더 최단거리면 업데이트 해준다
}
}
printf("%d\n", Table[End]); // 도착점까지의 최단거리
return 0;
}