정수론
- 정수의 성질을 연구하는 분야
- 약수와 배수
- 소수 판별
- 에라토스테네스의 체
- 소인수 분해
- 유클리드 호제법
- 파스칼 삼각형
<약수 구하기 구현>
#include <stdio.h>
int main() {
int n;
scanf("%d", &n);
for(int i = 1; i <= n; i++){
if(n%i ==0)
printf("%d ", i);
}
return 0;
}<소수> -> 약수가 자기 자신과 1만 존재하는 정수
소수 판별 구현
#include <stdio.h>
int main() {
int n;
scanf("%d", &n);
bool isPrime = true;
for(int i = 2; i < n; i++){
if(n % i == 0){
isPrime = false;
break;
}
}
if(isPrime)
printf("소수입니다");
else
printf("소수가 아닙니다");
return 0;
} < 에라토스테네스의 체 >
-> 소수를 구하는 알고리즘
배수들을 제거하는 과정을 반복해서 소수를 구한다
시간복잡도 : O(nlogn)
1~N 범위에서 소수를 구해라 -> 에라토스테네스의 체를 사용하면 빠르다
N인 소수냐? / 특정 수가 소수인지 판별하는 것은 1부터 루트N 까지 나누는 것이 더 빠르다
<소인수 분해>
-> 숫자 N을 소수의 곱으로 나타낸다
코드 구현 시 소수의 리스트를 미리 알지 않아도 소인수 분해 가능
2부터 차례대로 계속 나눠도 가능하다
ex > 60의 경우 우선 2로 가능할 때 까지 나눈다
60 / 2 = 30
30 / 2 = 15
2로 더이상 나눌 수 없으므로 그 다음 수인 3으로 나눈다
15 / 3 = 5
3으로 더이상 나눌 수 없으므로 그 다음 수인 4로 나눈다
2로 나눌 수 있을만큼 최대한으로 시도했기에 절대 나눠질 수 없다
소인수 분해 구현
#include <stdio.h>
int main() {
int n;
scanf("%d", &n);
for(int i = 2; n > 1; ){ // for문에서 i 자동 증가 방지
if(n % i == 0){
printf("%d ", i);
n /= i; // i로 나누는 것 반복
}
else{
i ++; // i로 더이상 나눠지지 않으므로 하나 증가 시켜 다음 수로 시도한다
}
}
return 0;
}<유클리드 호제법>
-> 최대공약수 를 구하기 위한 알고리즘
두 수 a, b 가 있다고 하자
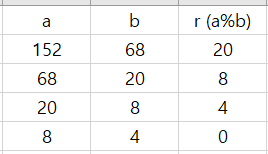
위와 같이 a를 b로 나눈 나머지를 새로운 b로 바꾼다
a는 이전의 b 값을 가져온다
이 과정을 반복해서 나머지가 0이 되는 순간 b 값이 처음 두 수의 최대공약수가 된다
유클리드 호제법 구현
#include <stdio.h>
int main() {
int a, b;
int GCD; // a와 b의 최대공약수
scanf("%d %d", &a, &b);
while(1){
int r = a % b;
if(r == 0){
GCD = b;
break;
}
a = b;
b = r;
}
printf("%d\n", GCD);
return 0;
}최소공배수는 최대공약수를 사용하여 구할 수 있다
최소공배수 x 최대공약수 = a x b
<파스칼의 삼각형>

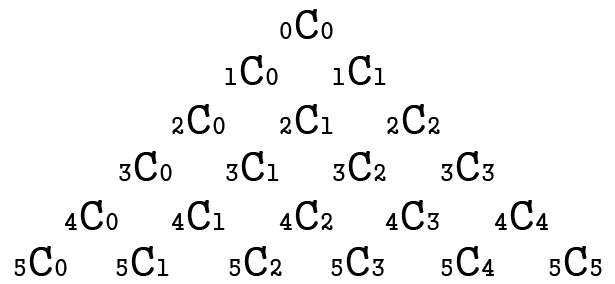
위 두 사진을 보면 파스칼의 삼각형은 행 별로 조합과 연관되어 있음을 알 수 있다
조합 문제에서 (ex> 20C11) 수가 커지는 경우 직접 나눠서 계산하는 것은 어려울 수 있다
파스칼의 삼각형을 사용해서 해결해보자
이미지출처
https://ko.wikipedia.org/wiki/%ED%8C%8C%EC%8A%A4%EC%B9%BC%EC%9D%98_%EC%82%BC%EA%B0%81%ED%98%95
https://5stralia.tistory.com/7
