큰 수의 법칙

정의

큰 수의 법칙(Law of large numbers, LLN)은 표본집단의 크기가 커지면 커질수록, 그 표본평균이 모평균에 가까워짐을 나타내는 법칙이다.

평균이 $\mu$, 분산이 $\sigma^2$이고 i.i.d.(독립항등분포)를 따르는 확률변수 $X_1, X_2, \cdots, X_n$가 있을 때, 그 표본평균 $\bar{X_n}$을 $(X_1 + X_2 + \cdots X_n)/n$이라고 했을 때, 큰 수의 법칙은 다음 두 가지로 설명할 수 있다.

• (약한 큰 수의 법칙) 임의의 $\epsilon > 0$이 존재하여,

  $\lim_{n \to \infty} P \left( |\bar{X}_n - \mu| > \epsilon \right) = 0$

  즉, $n$이 커지면 커질수록, 표본평균과 모평균은 한없이 가까워진다.

• (강한 큰 수의 법칙)

  $P\left(\lim_{n \to \infty}\bar{X}_n = \mu \right) = 1$

  약한 법칙과 거의 비슷하지만, 약간의 수학적인 차이가 존재한다.

---

증명

여기서는 약한 법칙에 대해서만 증명한다. 먼저, 체비쇼프 부등식에 의해, 임의의 확률변수 $X$와 그 확률변수의 평균 $\mu$, 임의의 상수 $\alpha$에 대하여

가 성립함을 알고 있다. 그리고, 중심극한정리의 유도과정에서, 표본평균 $\bar{X}_n$의 평균은 $\mu$, 분산은 $\frac{\sigma^2}{n}$의 형태로 계산됨을 보았다. 즉, 위 체비쇼프 부등식에서 확률변수 $X$를 표본평균 $\bar{X}_n$로 치환하면, 다음을 얻는다.

여기서 $n \to \infty$일 때, 위 식의 우변은 0으로 수렴한다. 즉,

이 된다. 이로서 우리가 보이고자 하는 약한 큰 수의 법칙이 보여졌다.

---

의의

큰 수의 법칙은 시행 횟수가 늘어날수록, 시행으로 인해 실제 측정된 확률과 수학적으로 예측된 확률이 점점 같아짐을 이론적으로 보증해준다. 이는 나아가서 통계학 전반에 대한 귀납적인 추론에 대한 이론적인 기반이 된다.

---

예시

예를 들어, 앞뒤면이 나올 확률이 같은 동전을 던진다고 생각해보자. 이 때 동전을 던져서 앞면이 나올 확률은 당연히 $1/2$이지만, 시행 회수가 적으면 $1/2$에서 다소 떨어진 확률 측정값이 나올 수도 있다. 하지만 시행을 충분히 많이 반복하면 큰 수의 법칙에 의해 반드시 그 확률은 $1/2$로 수렴한다. 다음은 해당 예제를 python 코드로 구현한 예제이다.

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt

for i in range(5):
    prob = []
    count = 0
    for i in range(1, 1001):
        num = np.random.randint(2)
        if num == 1:
            count += 1
        prob.append(count / i)
    
    prob_df = pd.DataFrame(prob)
    
    plt.plot(prob_df)

plt.title('LLN Test')
plt.xlabel('Flip count')
plt.ylabel('Probability')
plt.ylim(0, 1)
plt.show()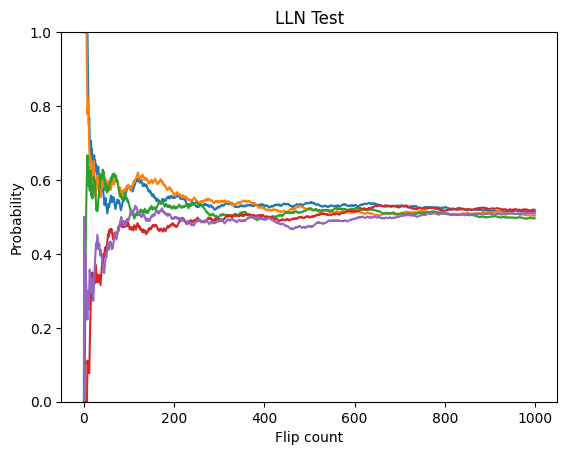

동전을 1000번 던져서 그 확률을 구하는 시행을 5회 반복하였다. 그래프에서 알 수 있듯이, 처음에는 앞면이 나올 확률에 다소 오차가 있지만 시행을 충분히 많이 함에 따라 그 값은 $0.5$에 수렴하는 것을 볼 수 있다.

---

중심극한정리와의 차이

모집단에 대한 직접적인 정보 없이 표본평균에 대한 정보를 준다는 점에서 중심극한정리와 닮아있지만, 큰 수의 법칙은 표본평균의 값에 대해 직접적인 정보를 줄 뿐이지만, 중심극한정리는 표본평균에 대한 분포 정보를 준다는 차이점이 있다.