[algorithm] Union Find

sinbom·2021년 3월 14일

Union Find

각 노드 간 연결성을 파악하는 dynamic connectivity 문제를 해결하기 위한 알고리즘이다. 복잡하게 얽힌 네트워크 속에서 특정 노드들 간의 연결 여부를 확인해야할 때, 효과적으로 문제를 해결할 수 있다. 노드의 연결 여부를 확인하는 것에만 중점을 두며, 거리 또는 최단 거리 등 연결 여부 외 다른 정보에는 관심을 갖지 않는다.

구현 연산은 다음과 같다.

union command: 두 노드를 연결한다.
find/connected query: 두 노드의 연결 여부를 확인한다.

여기서 "연결"은 다음의 등가 관계를 가정한다.

reflexive: A는 B와 연결되어 있다.
symmetric: A가 B와 연결되어 있다면 B도 A와 연결되어 있다.
transitive: A가 B와 연결되어 있고 B가 C와 연결되어 있다면 A와 C도 연결되어 있다.

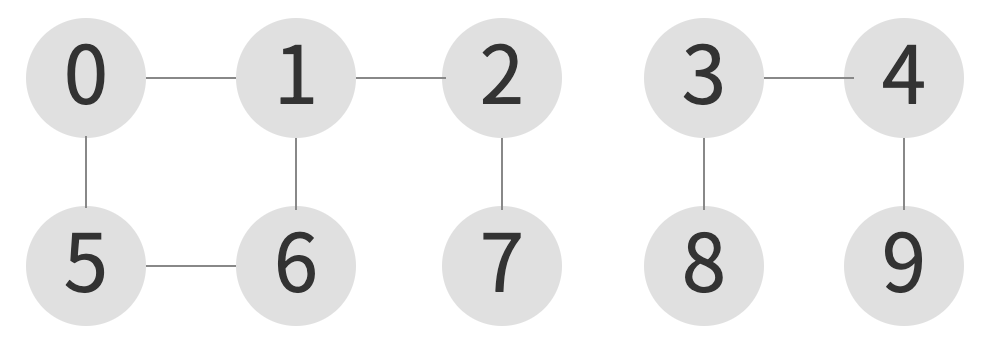
위 그림을 union, connected 연산을 통해 나타내면 다음과 같다.

union(3, 4)
union(3, 8)
union(5, 6)
union(4, 9)
union(1, 2)
union(0, 5)
union(2, 7)
union(1, 6)
union(0, 1)

connected(8, 1) => false
connected(8, 9) => true
connected(0, 7) => true

{0, 1, 2, 5, 6, 7} {3, 4, 8, 9} => connected components

array, tree 등을 사용해서 구현할 수 있는 disjoint set 자료구조를 사용한다. array를 통해 구현하는 경우 index는 노드를 의미하고, element는 노드와 연결된 노드를 의미한다.

disjoint set은 서로 중복되는 공통 원소가 없는 상호 배타적인 부분 집합들로 나눠진 원소들을 표현할 수 있는 자료구조이다.

알고리즘을 구현하기 위한 API 설계는 다음과 같다.

void init(int n): N개의 노드를 초기화한다.
int root(int i): 노드가 속한 트리의 루트 노드를 반환한다.
void union(int a, int b): 두 노드를 연결한다.
boolean connected(int a, int b): 두 노드의 연결 여부를 확인한다.

Quick Find

union find를 구현한 가장 간단한 알고리즘이다. 노드가 연결될 때마다 모든 노드를 순회하면서 연결된 노드를 변경한다.

init(10)

index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	3	4	5	6	7	8	9

union(1, 0)

index	0	1	2	3	4	5	6	7	8	9
element	0	0	2	3	4	5	6	7	8	9

union(4, 3)

index	0	1	2	3	4	5	6	7	8	9
element	0	0	2	3	3	5	6	7	8	9

union(2, 4)

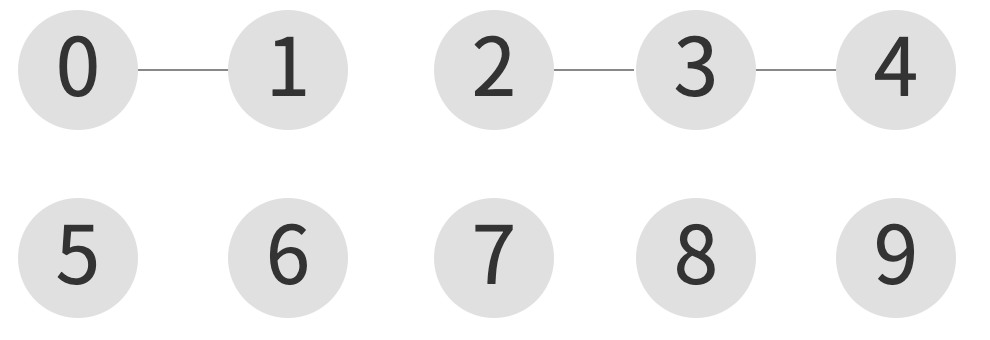
index	0	1	2	3	4	5	6	7	8	9
element	0	0	3	3	3	5	6	7	8	9

union(7, 3)

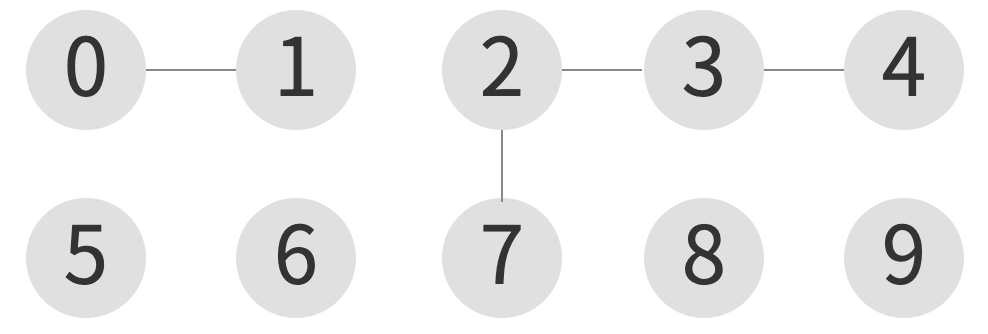
index	0	1	2	3	4	5	6	7	8	9
element	0	0	3	3	3	5	6	3	8	9

union(7, 0)

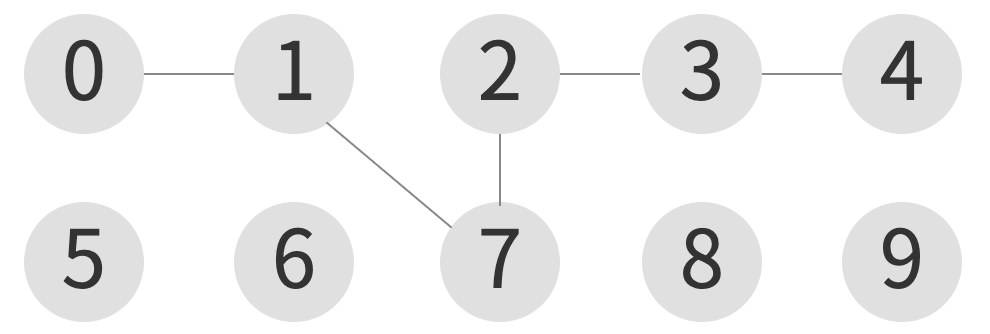
index	0	1	2	3	4	5	6	7	8	9
element	0	0	0	0	0	5	6	0	8	9

코드 구현

public class QuickFind {

    private int[] nodes;

    public QuickFind(int n) {
        init(n);
    }

    public void init(int n) {
        nodes = new int[n];
        for (int i = 0; i < n; i++) {
            nodes[i] = i;
        }
    }

    public boolean connected(int a, int b) {
        return nodes[a] == nodes[b];
    }

    public void union(int a, int b) {
        int aNode = nodes[a];
        int bNode = nodes[b];
        for (int i = 0; i < nodes.length; i++) {
            if (nodes[i] == aNode) {
                nodes[i] = bNode;
            }
        }
    }

}

init: 모든 노드를 순회하면서 초기화하고, N개의 데이터를 저장할 수 있는 메모리가 필요하다. 시간 복잡도는 O(N)이다.
union: 모든 노드를 순회하면서 연결된 노드를 변경한다. 시간 복잡도는 O(N)이다.
connected: 두 노드의 연결 여부를 확인한다. 시간 복잡도는 O(1)이다.
union 연산이 모든 노드를 순회하기 때문에 비효율적이다.

Quick Union

quick find 알고리즘의 union 연산을 개선하기 위한 알고리즘이다. 노드가 속한 집합을 트리 구조로 형성하고, 노드가 속한 트리의 루트 노드와 연결된 노드만 변경한다.

init(10)

index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	3	4	5	6	7	8	9

union(7, 2)

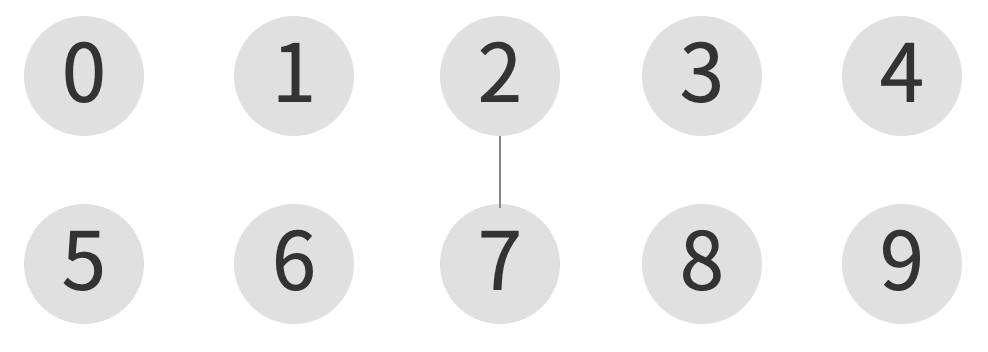
index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	3	4	5	6	2	8	9

union(3, 8)

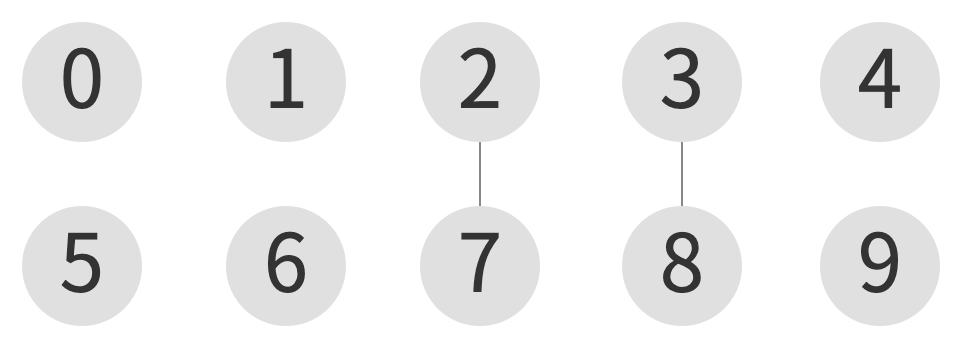
index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	8	4	5	6	2	8	9

union(9, 4)

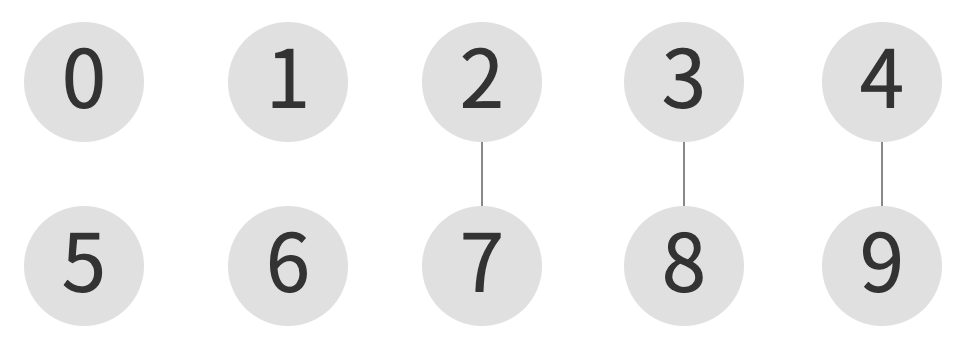
index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	8	4	5	6	2	8	4

union(3, 7)

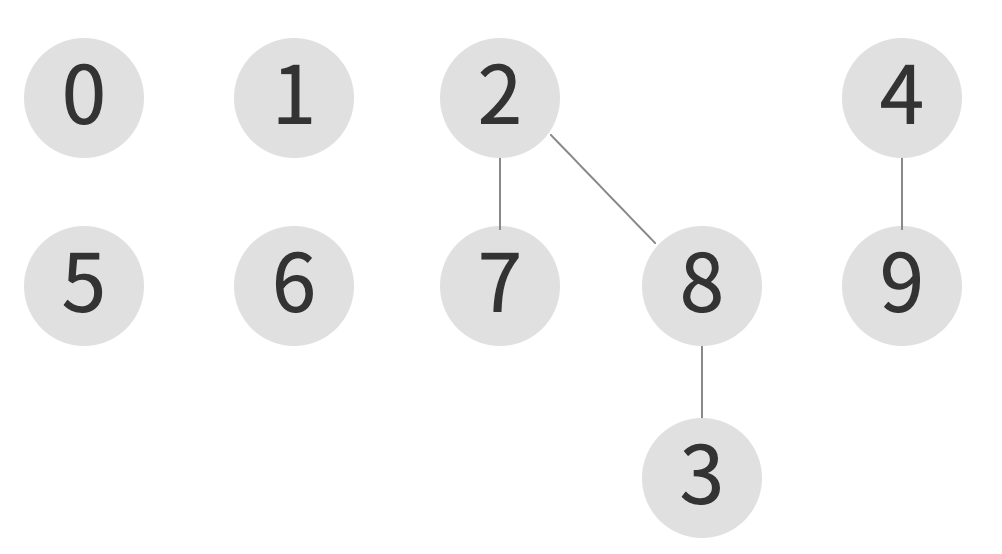
index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	8	4	5	6	2	2	4

union(9, 3)

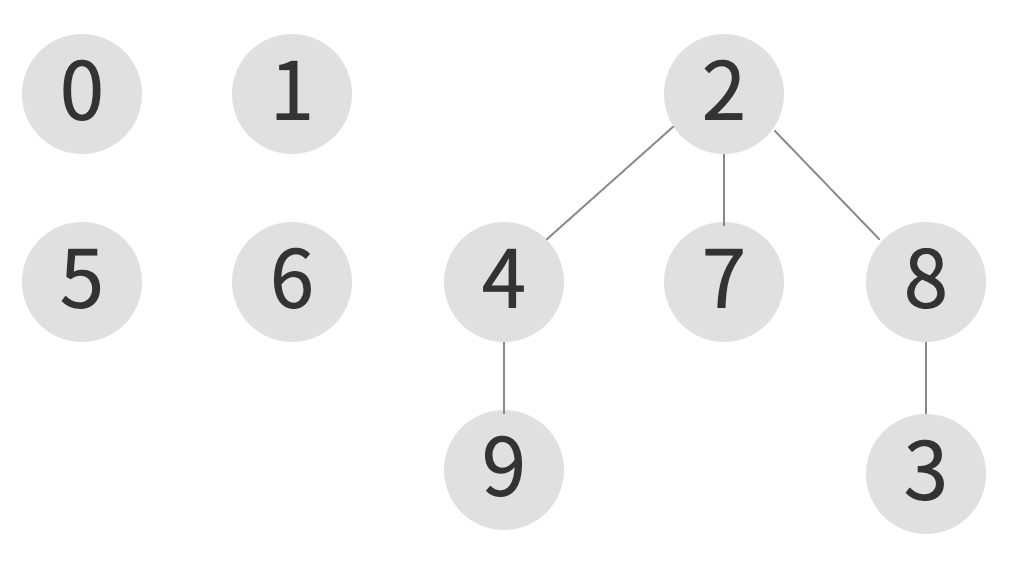
index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	8	2	5	6	2	2	4

union(0, 5) -> union(6, 5) -> union(1, 2) -> union(0, 1)

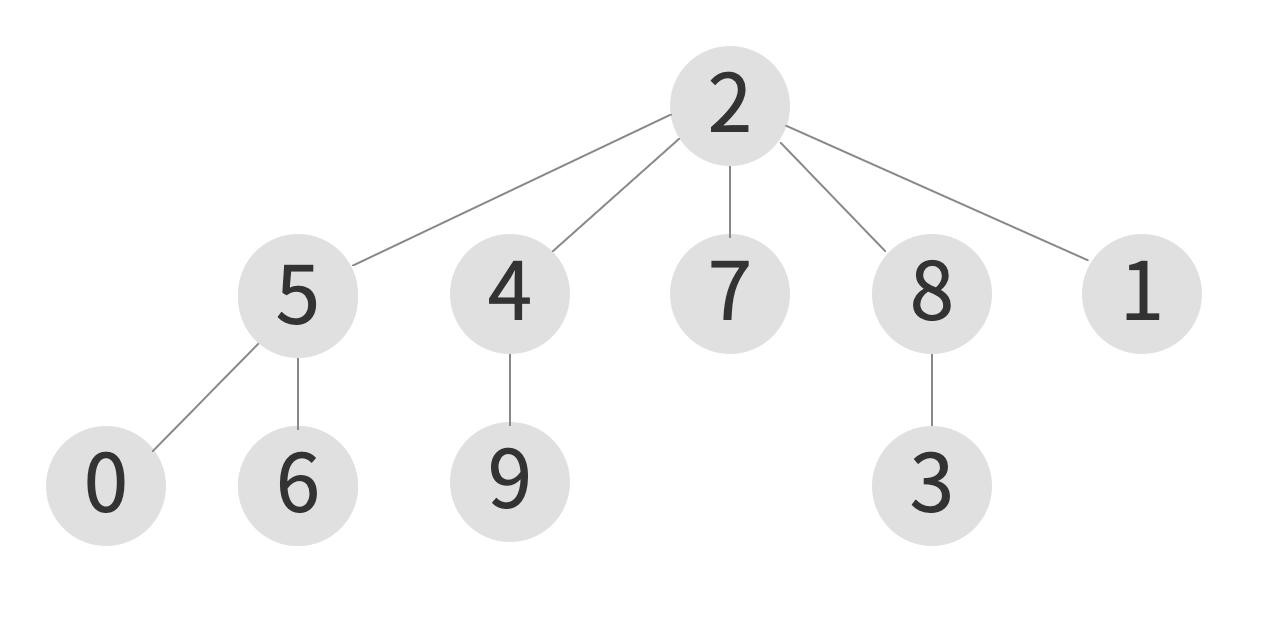
index	0	1	2	3	4	5	6	7	8	9
element	5	2	2	8	2	2	5	2	2	4

코드 구현

public class QuickUnion {

    private int[] nodes;
    
    public QuickUnion(int n) {
        init(n);
    }

    public void init(int n) {
        nodes = new int[n];
        for (int i = 0; i < n; i++) {
            nodes[i] = i;
        }
    }

    private int root(int i) {
        while (i != nodes[i]) {
            i = nodes[i];
        }
        return i;
    }

    public boolean connected(int a, int b) {
        return root(a) == root(b);
    }

    public void union(int a, int b) {
        int i = root(a);
        int j = root(b);
        nodes[i] = j;
    }

}

init: 모든 노드를 순회하면서 초기화하고, N개의 데이터를 저장할 수 있는 메모리가 필요하다. 시간 복잡도는 O(N)이다.
root: 노드가 속한 트리의 루트 노드를 반환한다. 시간 복잡도는 O(N)이다.
union: 노드가 속한 트리의 루트 노드와 연결된 노드만을 변경한다. 시간 복잡도는 O(N)이다.
connected: 두 노드의 연결 여부를 확인한다. 시간 복잡도는 O(N)이다.
connected 연산의 시간 복잡도는 증가하였으나, union 연산이 모든 노드들을 순회하지 않고 변경이 필요한 노드만 변경한다.

균형이 무너진 선형 구조의 트리

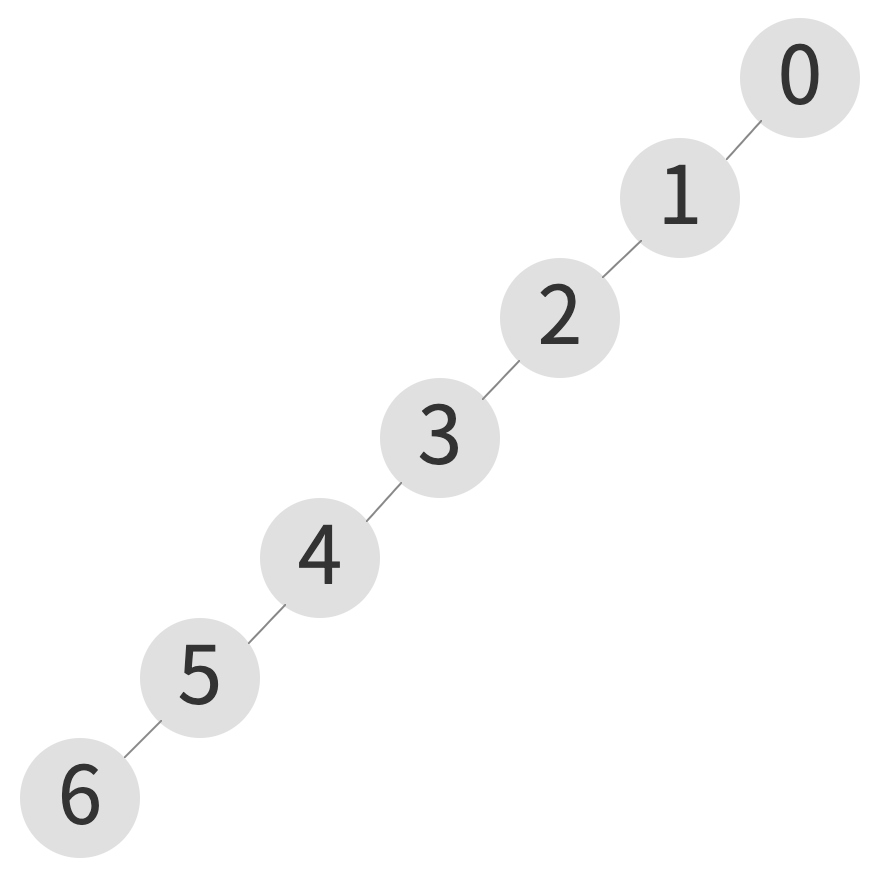
index	0	1	2	3	4	5	6
element	0	0	1	2	3	4	5

노드를 연결하는 과정에서 형성되는 트리가 균형이 무너진 선형 구조로 형성될 수 있다.
루트 노트까지 이동하려면 최악의 경우 선형 시간만큼 소모되기 때문에 union, connected 연산의 시간 복잡도는 O(N)이다.

Weighted Quick Union

quick union 알고리즘의 union 연산을 개선하기 위한 알고리즘이다. 크기가 작은 트리를 크기가 큰 트리로 병합해서 트리의 전체 높이가 증가하는 것을 최소화하여 균형이 무너지는 것을 방지할 수 있다.

init(10)

index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	3	4	5	6	7	8	9

union(2, 7)

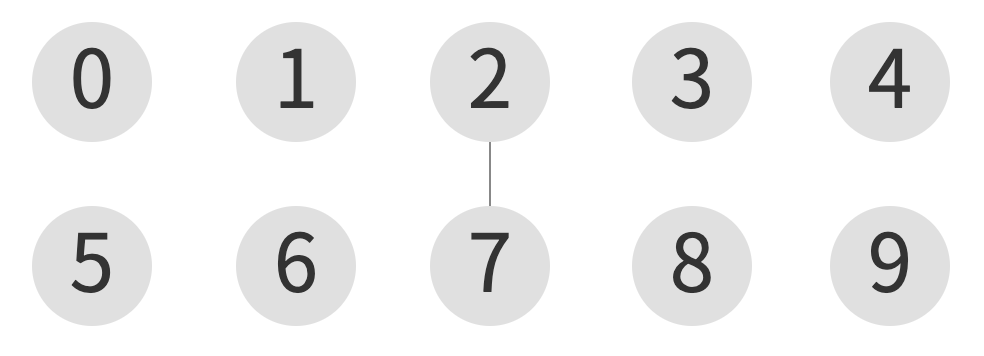
index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	3	4	5	6	2	8	9

union(3, 8)

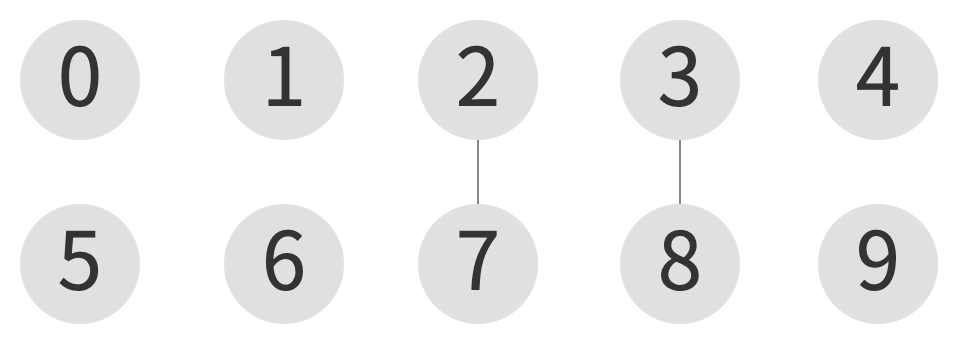
index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	3	4	5	6	2	3	9

union(4, 9)

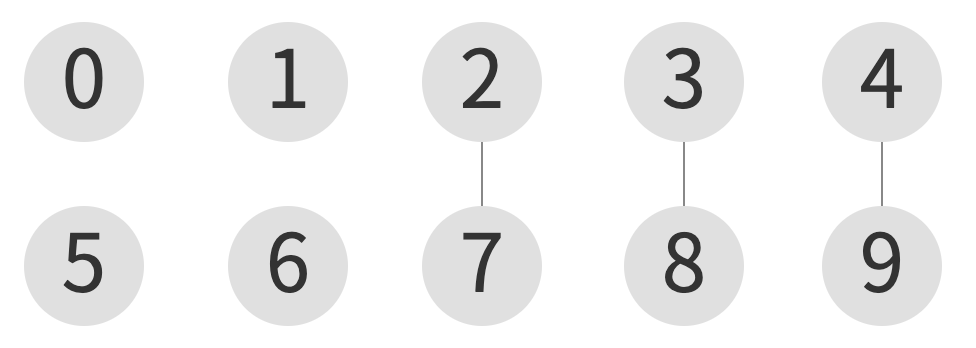
index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	3	4	5	6	2	3	4

union(6, 7)

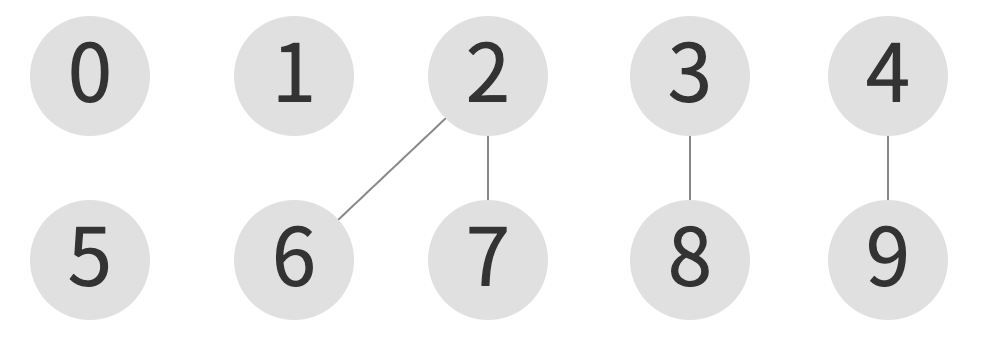
index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	3	4	5	2	2	3	4

union(7, 3)

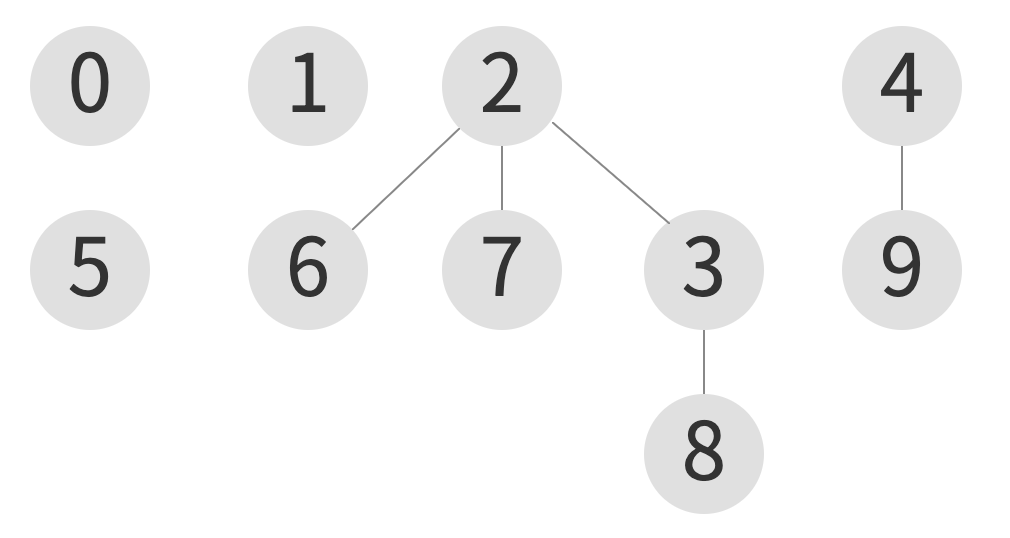
index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	2	4	5	2	2	3	4

union(9, 8)

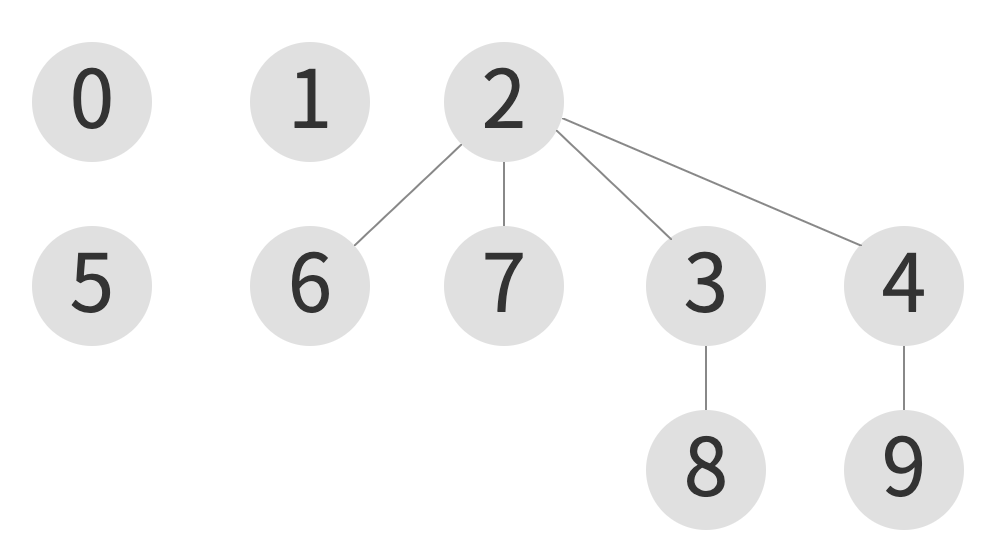
index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	2	2	5	2	2	3	4

union(0, 1) -> union(5, 0) -> union(6, 0)

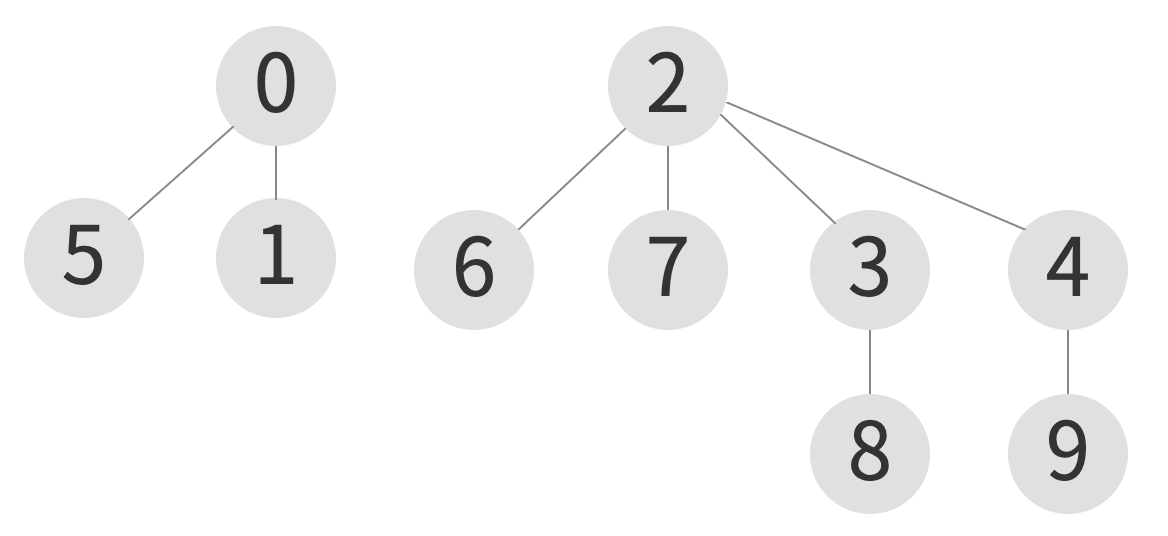
index	0	1	2	3	4	5	6	7	8	9
element	0	0	2	2	2	0	2	2	3	4

union(9, 5) - case: weighted quick union

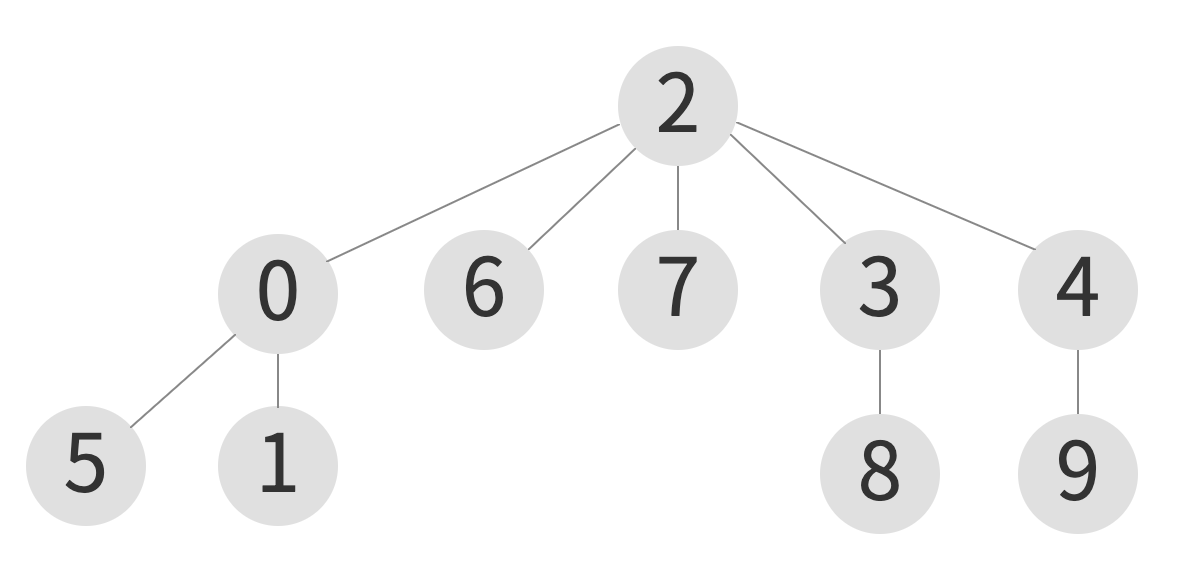
index	0	1	2	3	4	5	6	7	8	9
element	2	0	2	2	2	0	2	2	3	4

union(9, 5) - case: quick union

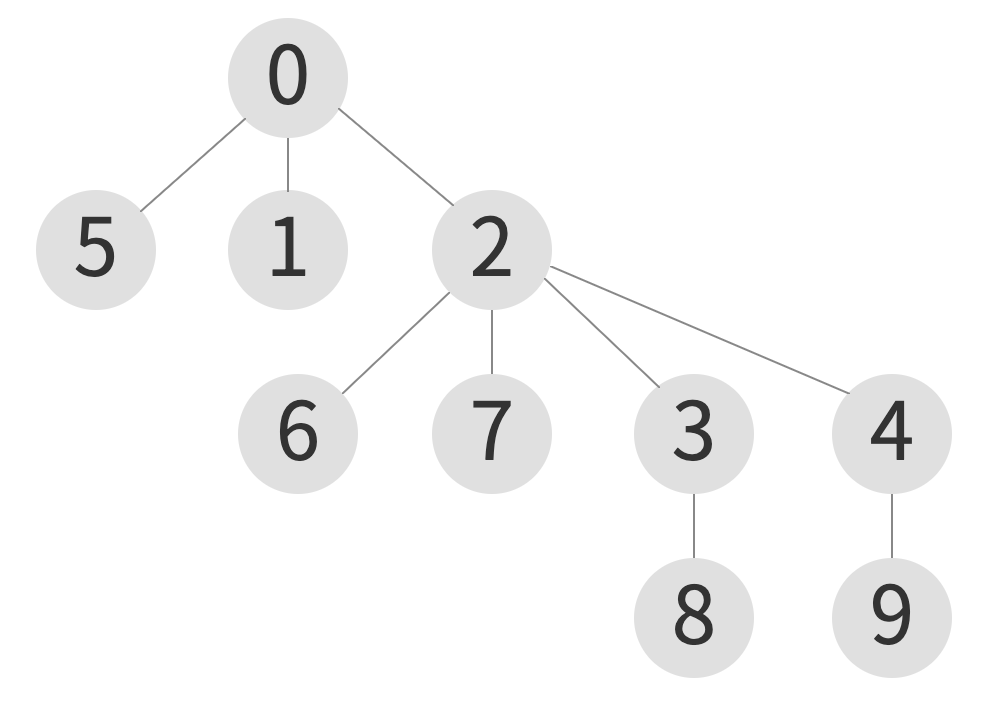
index	0	1	2	3	4	5	6	7	8	9
element	0	0	0	2	2	0	2	2	3	4

코드 구현

public class WeightedQuickUnion {

    private int[] nodes;

    private int[] sizes;

    public WeightedQuickUnion(int n) {
        init(n);
    }

    public void init(int n) {
        this.nodes = new int[n];
        for (int i = 0; i < n; i++) {
            nodes[i] = i;
            sizes[i] = 1;
        }
    }

    private int root(int i) {
        while (i != nodes[i]) {
            i = nodes[i];
        }
        return i;
    }

    public boolean connected(int a, int b) {
        return root(a) == root(b);
    }

    public void union(int a, int b) {
        int i = root(a);
        int j = root(b);
        if (i == j) {
            return;
        }
        if (sizes[i] < sizes[j]) {
            nodes[i] = j;
            sizes[j] += sizes[i];
        } else {
            nodes[j] = i;
            sizes[i] += sizes[j];
        }
    }

}

init: 모든 노드를 순회하면서 초기화하고, 2N개의 데이터를 저장할 수 있는 메모리가 필요하다. 시간 복잡도는 O(N)이다.
root: 노드가 속한 트리의 루트 노드를 반환한다. 시간 복잡도는 O(log ${_2}^{N}$ )이다.
union: 노드가 속한 트리 중 크기가 작은 트리를 크기가 큰 트리로 병합한다. 시간 복잡도는 O(log ${_2}^{N}$ )이다.
connected: 두 노드의 연결 여부를 확인한다. 시간 복잡도는 O(log ${_2}^{N}$ )이다.
각 노드가 속한 트리의 크기를 저장하는 메모리가 추가적으로 필요하다.

시간 복잡도 O(log ${_2}^{N}$ )에 대한 증명

트리의 높이	0	1	2	3	4	5	...	log ${_2}^{N}$
트리의 크기	1	2	4	8	16	32	...	N

union 연산시 병합되는 트리의 높이가 1만큼 증가하는데, 이것은 트리의 노드들이 루트 노드까지의 이동 거리가 1씩 증가하는 것과 같다.
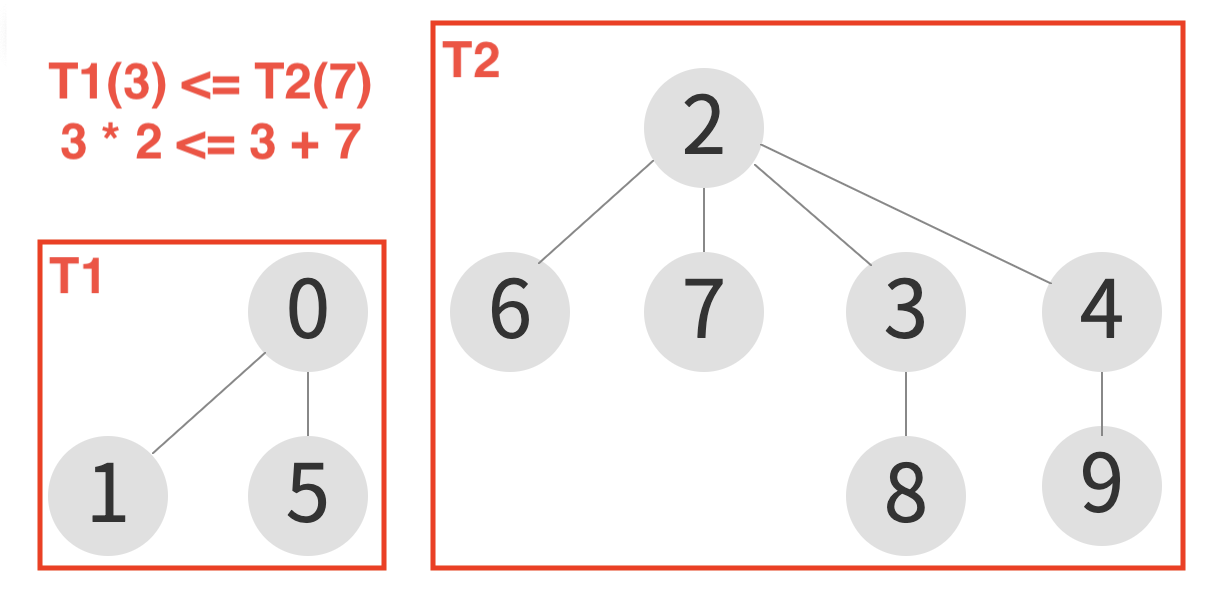
병합되는 트리의 높이가 1씩 증가하기 때문에 크기가 큰 트리(T2)가 작은 트리(T1)를 병합해야 전체 트리의 높이가 길어지는 것을 방지할 수 있다.
트리가 병합되면서 최소한의 트리 크기를 형성하는 경우는 두 트리의 크기가 같은 경우이다. T1 + T2 = T1 * 2
즉, 트리가 계속해서 병합되어도 트리의 크기가 N일 때 형성될 수 있는 가장 높은 높이는 log ${_2}^{N}$ 이다.

Weighted Quick Union With Path Compression

quick union 알고리즘을 더욱 개선하기 위한 알고리즘이다. 연산시 루트 노드까지의 경로를 압축시켜 지속적으로 트리의 높이를 낮은 형태로 재구성한다.

init(10)

index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	3	4	5	6	7	8	9

union(2, 7)

index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	3	4	5	6	2	8	9

union(3, 8)

index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	3	4	5	6	2	3	9

union(4, 9)

index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	3	4	5	6	2	3	4

union(6, 7)

index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	3	4	5	2	2	3	4

union(7, 3)

index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	2	4	5	2	2	3	4

union(9, 8)

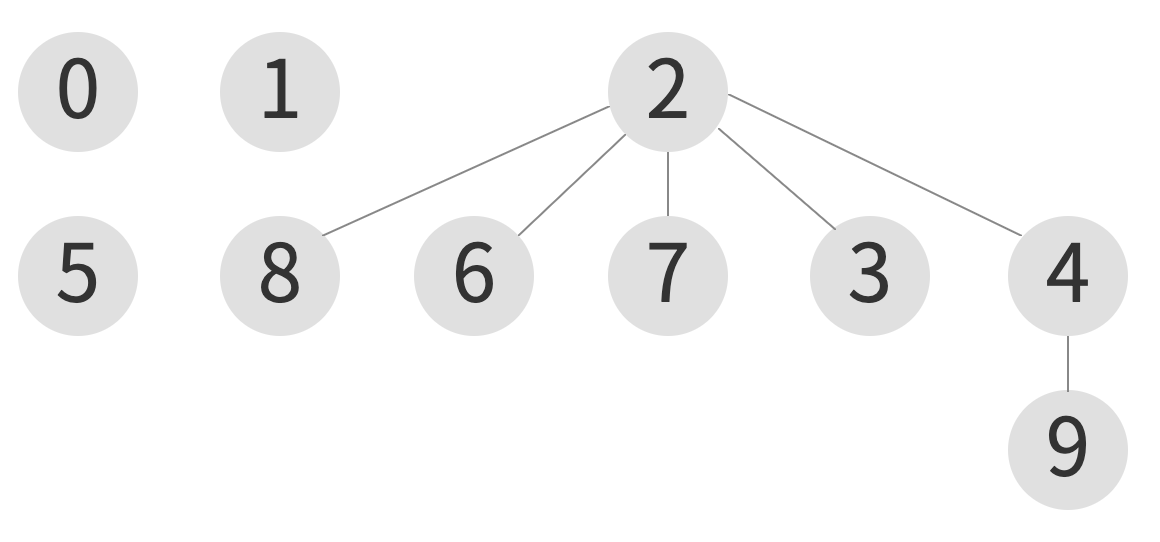
index	0	1	2	3	4	5	6	7	8	9
element	0	1	2	2	2	5	2	2	2	4

union(0, 1) -> union(5, 0) -> union(6, 0)

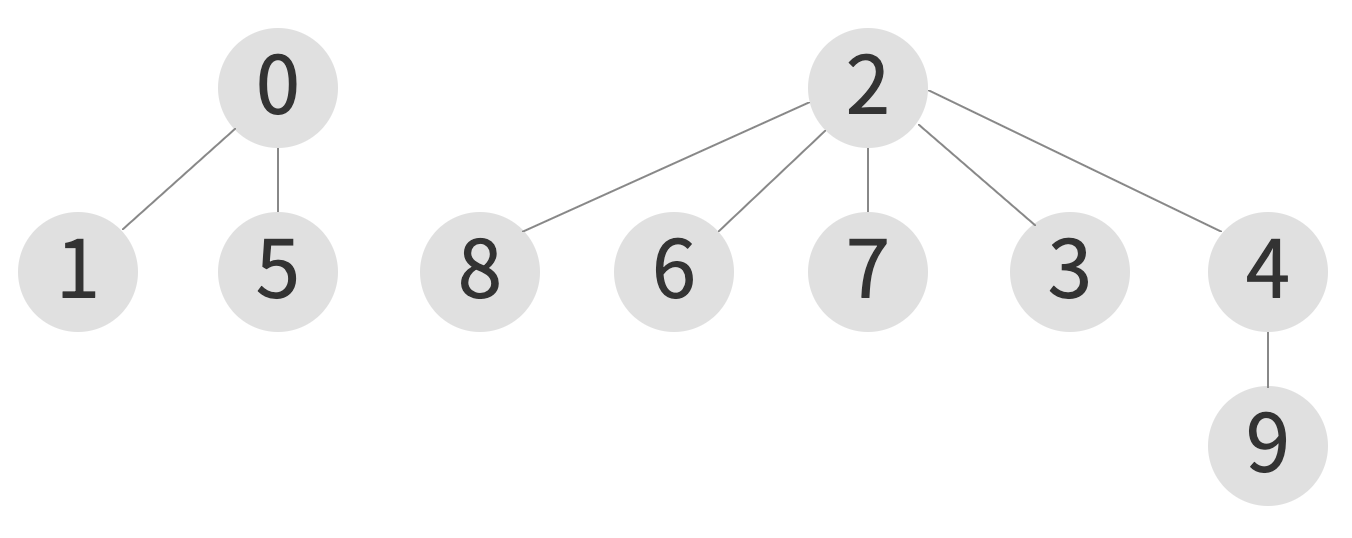
index	0	1	2	3	4	5	6	7	8	9
element	0	0	2	2	2	0	2	2	2	4

union(9, 5)

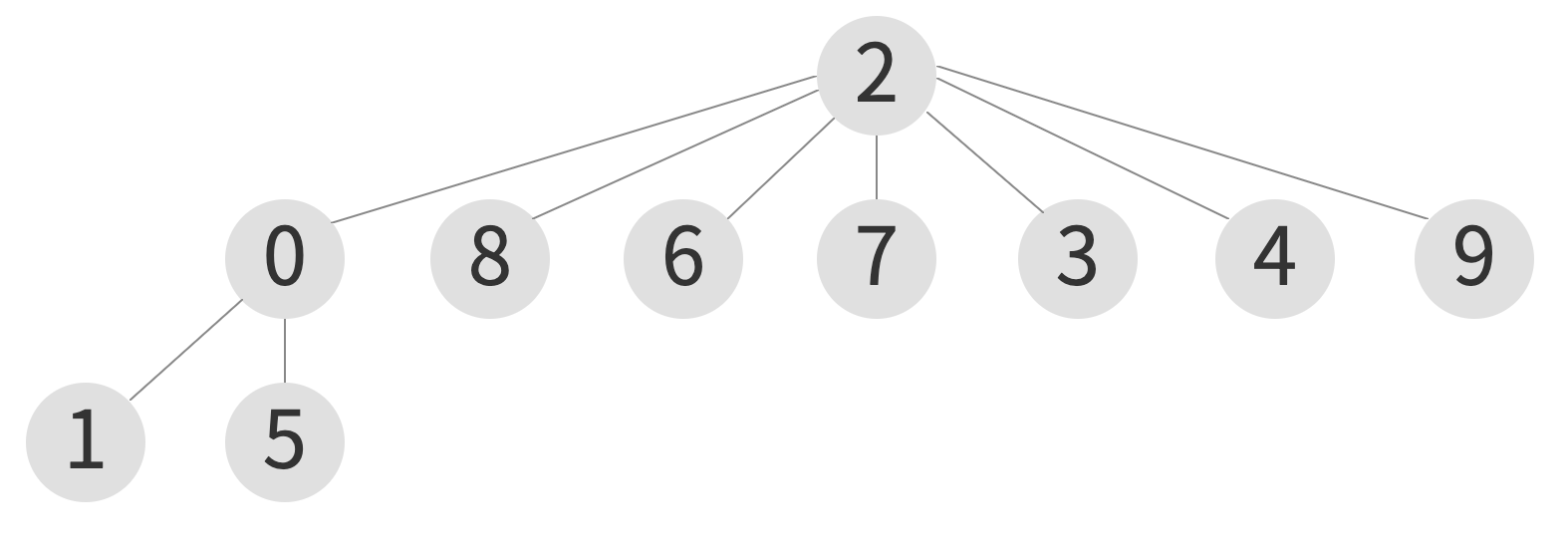
index	0	1	2	3	4	5	6	7	8	9
element	2	0	2	2	2	0	2	2	2	2

connected(1, 5)

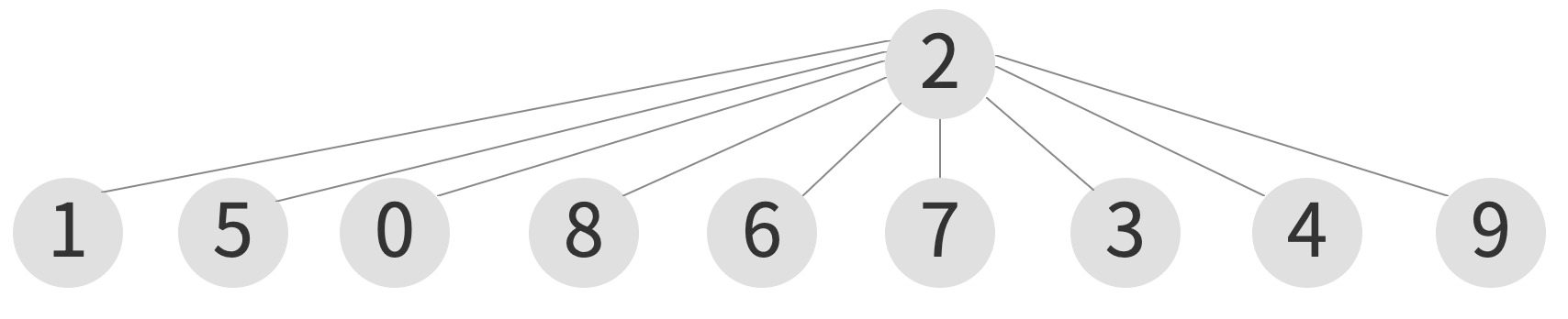
index	0	1	2	3	4	5	6	7	8	9
element	2	2	2	2	2	2	2	2	2	2

코드 구현

public class WeightedQuickUnionWithPathComperssion {

    private int[] nodes;

    private int[] sizes;

    public WeightedQuickUnionWithPathComperssion(int n) {
        init(n);
    }

    public void init(int n) {
        this.nodes = new int[n];
        for (int i = 0; i < n; i++) {
            nodes[i] = i;
            sizes[i] = 1;
        }
    }

    private int root(int i) {
        while (i != nodes[i]) {
            nodes[i] = nodes[nodes[i]];
            i = nodes[i];
        }
        return i;
    }

    public boolean connected(int a, int b) {
        return root(a) == root(b);
    }

    public void union(int a, int b) {
        int i = root(a);
        int j = root(b);
        if (i == j) {
            return;
        }
        if (sizes[i] < sizes[j]) {
            nodes[i] = j;
            sizes[j] += sizes[i];
        } else {
            nodes[j] = i;
            sizes[i] += sizes[j];
        }
    }

}

init: 모든 노드를 순회하면서 초기화하고, 2N개의 데이터를 저장할 수 있는 메모리가 필요하다. 시간 복잡도는 O(N)이다.
root: 노드가 속한 트리의 루트 노드를 반환하는 과정에서 부모 노드와 연결되었던 노드를 조부모 노드와 연결되도록 재구성하여 루트 노드까지의 경로를 압축한다. 시간 복잡도는 O(log ${_2}^{N}$ )이다.
union: 노드가 속한 트리 중 크기가 작은 트리를 크기가 큰 트리로 병합하고, 그 과정에서 경로를 압축한다. 시간 복잡도는 O(log ${_2}^{N}$ )이다.
connected: 두 노드의 연결 여부를 확인하고, 그 과정에서 경로를 압축한다. 시간 복잡도는 O(log ${_2}^{N}$ )이다.
경로가 지속적으로 압축되어 모든 노드들이 루트 노드와 가까워진다면 최선의 경우 시간 복잡도 O(1)이다.

경로 압축의 효율성

알고리즘	시간 복잡도(N개의 노드 init + M번의 union)
Quick Find	N M
Quick Union	N M
Weighted Quick Union	N + M log ${_2}^{N}$
Quick Union With Path Compression	N + M log ${_2}^{N}$
Weighted Quick Union With Path Compression	N + M log $^{*}$ N

N개의 노드 init, M번의 union 연산을 수행했을 때, 시간 복잡도는 O(N + M log $^{*}$ N)이다. log $^{*}$ N의 증가 속도가 매우 느리기 때문에 선형 시간 복잡도는 아니지만 그것에 가까운 시간 복잡도라고 할 수 있다.

log $^{*}$ N(iterated logarithm, log star)는 N의 로그 함수를 수행한 결과 값을 반복적으로 수행해서 결과 값이 1이하가 나올때까지 수행된 횟수이다.
ex) N = 65536, log $^{*}$ N = 4 (log ${_2}^{65536}$ -> log ${_2}^{16}$ -> log ${_2}^{4}$ -> log ${_2}^{2}$ )

sinbom

Backend Developer

다음 포스트

[algorithm] Union Find

Union Find

Quick Find

코드 구현

Quick Union

코드 구현

균형이 무너진 선형 구조의 트리

Weighted Quick Union

코드 구현

시간 복잡도 O(log ${_2}^{N}$ )에 대한 증명

Weighted Quick Union With Path Compression

코드 구현

경로 압축의 효율성

[ps] 디스크 컨트롤러

0개의 댓글

[algorithm] Union Find

Union Find

Quick Find

코드 구현

Quick Union

코드 구현

균형이 무너진 선형 구조의 트리

Weighted Quick Union

코드 구현

시간 복잡도 O(log2N{_2}^{N}2​N)에 대한 증명

Weighted Quick Union With Path Compression

코드 구현

경로 압축의 효율성

[ps] 디스크 컨트롤러

0개의 댓글

시간 복잡도 O(log ${_2}^{N}$ )에 대한 증명