BST(Binary Search Tree), 이진탐색트리

ejklike님 블로그를 참고하여 공부한 내용을 정리했습니다!

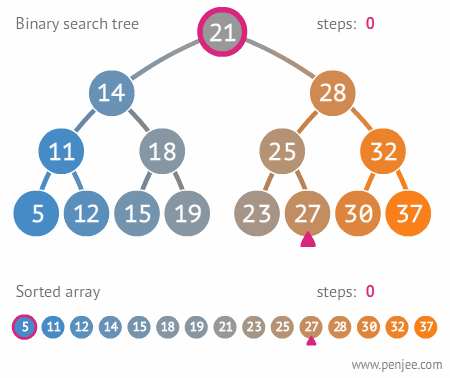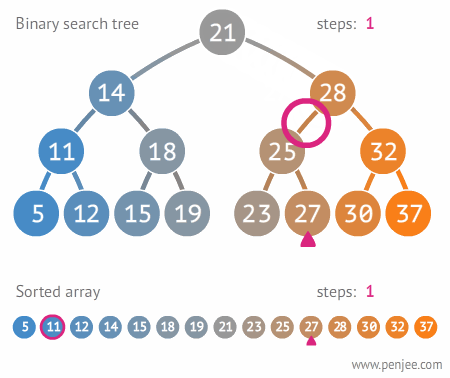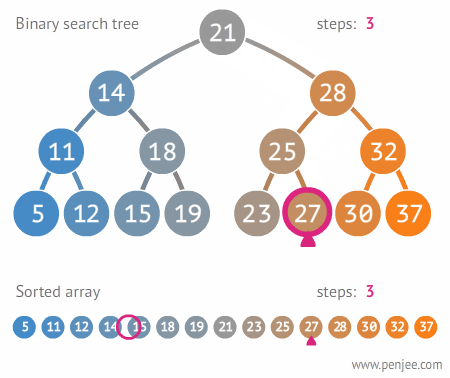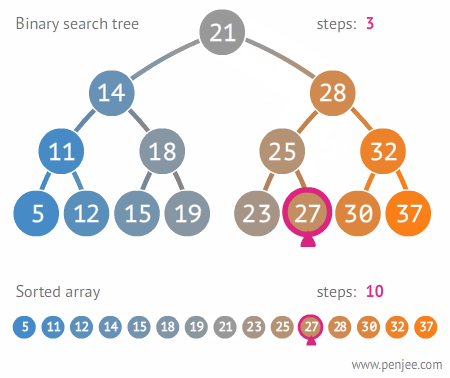
이진탐색트리를 사용하여 탐색/삽입/삭제를 시행할 때의 시간복잡도는 O(log n) 이다. 따라서 효율적인 탐색이 가능할 수 있다.

class Node(object):
    def __init__(self,data):
        self.data = data # 노드 값
        self.left = self.right = None # 좌/우 노드 (비어있음)

    

class BinarySearchTree(object):
    def __init__(self):
        self.root = None

    # 원소를 추가, 삭제, 탐색할 수 있도록 insert() delete() find() 메소드를 추가하자

    # 추가
    def insert(self,data):
        self.root = self._insert_value(self.root, data)
        return self.root is not None

    def _insert_value(self,node,data):
        if node is None:
            node = Node(data)
        else:
            if data <= node.data:
                node.left = self._insert_value(node.left, data)
            else:
                node.right = self._insert_value(node.right, data)

        return node

    # 탐색 (있는지 없는지, boolean 반환)
    def find(self, key): # 찾는 값이 key겠지?
        return self._find_value(self.root,key)

    def _find_value(self, root, key):
        if (root is None) or (root.data == key):
            return root is not None
        elif key < root.data:
            return self._find_value(root.left, key)
        else:
            return self._find_value(root.right, key)
    
    # 삭제
    def delete(self,key):
        self.root, deleted = self._delete_value(self.root,key)

        return deleted

    def _delete_value(self, node, key):
        if node is None:
            return node, False
        
        deleted = False

        # 찾은 경우
        if key==node.data: 
            deleted = True
            # 해당 노드의 오/왼이 모두 있는경우 
            if node.left and node.right:
                # replace the node to the leftmost of node.right
                parent, child = node, node.right
                while child.left is not None:
                    parent, child = child, child.left
                child.left = node.left
                if parent != node:
                    parent.left = child.right
                    child.right = node.right
                node = child
            # 오/왼 둘중 하나만 있는 경우
            elif  node.left or node.right:
                node = node.left or node.right
            # 둘 다 없는경우
            else:
                node = None

        # 작은 경우
        elif key < node.data: 
            node.left, deleted = self._delete_value(node.left, key)
        
        # 큰 경우
        else: 
            node.right, deleted = self._delete_value(node.right, key)

        return node, deleted
        
        
    # 순회! 
    
    # Depth First Traversal (DFS) 깊이 우선 순회 > 전위, 정위, 후위

	# 전위순회 (root > left > right)
    def pre_order_traversal(self):
        def _pre_order_traversal(root):
            if root is None:
                # pass
                print('None',end=' ')
            else:
                print(root.data,end=' ')
                _pre_order_traversal(root.left)
                _pre_order_traversal(root.right)

        _pre_order_traversal(self.root)

    # 정위순회 (left > root > right)
    def in_order_traversal(self):
        def _in_order_traversal(root):
            if root is None:
                # pass
                print('None',end=' ')
            else:
                _in_order_traversal(root.left)
                print(root.data,end=' ')
                _in_order_traversal(root.right)
        _in_order_traversal(self.root)

    # 후위순회 (left > right > root)
    def post_order_traversal(self):
        def _post_order_traversal(root):
            if root is None:
                # pass
                print('None',end=' ')
            else:
                _post_order_traversal(root.left)
                _post_order_traversal(root.right)
                print(root.data,end=' ')
        _post_order_traversal(self.root)


    # 너비 우선 순회 (Breadth First Traversal)
    # 레벨 순회
    def level_order_traversal(self):
        def _level_order_traversal(root):
            queue = [root]

            while queue:
                root = queue.pop(0)

                if root is not None:
                    print(root.data)
                    if root.left:
                        queue.append(root.left)
                    if root.right:
                        queue.append(root.right)

        _level_order_traversal(self.root)


# 실행부
array = [40,4,34,45,14,55,48,13,15,49,47]

bst = BinarySearchTree()

for i in array:
    bst.insert(i)

print(bst.find(15))
print(bst.delete(15))
print(bst.find(15))

삭제 부분의 이해가 조금 어렵다. (특히 child가 2개일 경우)

다 이해했다면 이런 문제도 풀어보자!
https://practice.geeksforgeeks.org/problems/insert-a-node-in-a-bst/1

참조
https://ejklike.github.io/2018/01/09/traversing-a-binary-tree-2.html
https://www.fun-coding.org/Chapter10-tree.html