힙을 왜써?
힙은 최댓값이나 최솟값을 빠르게 얻어내어야 하는 상황에서 사용된다.
파이썬에서 정렬 sort()은 'Tim sort' 라는 방식을 사용하는데, 이 때 시간복잡도는 nlogn 이다. 반면 힙을 사용해서 최대/최솟값을 얻어낼 경우 logn의 시간복잡도를 갖기 때문에, 아래 그래프를 참고하면 엄청난 속도의 차이를 경험할 수 있게 된다.
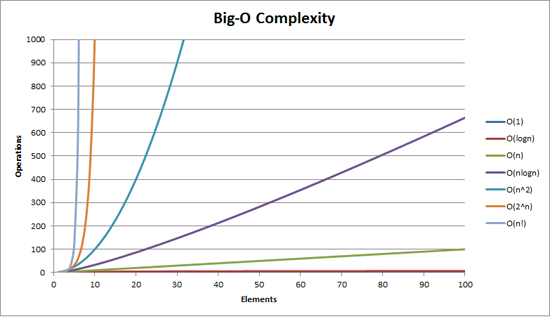
똑같이 log 가 들어있지만 logn의 시간복잡도는 땅에 붙어있는 반면 nlogn은 원소의 갯수에 거의 정비례하는 것을 확인할 수 있다.
힙이 머야?
힙은 이렇게 생겼다.
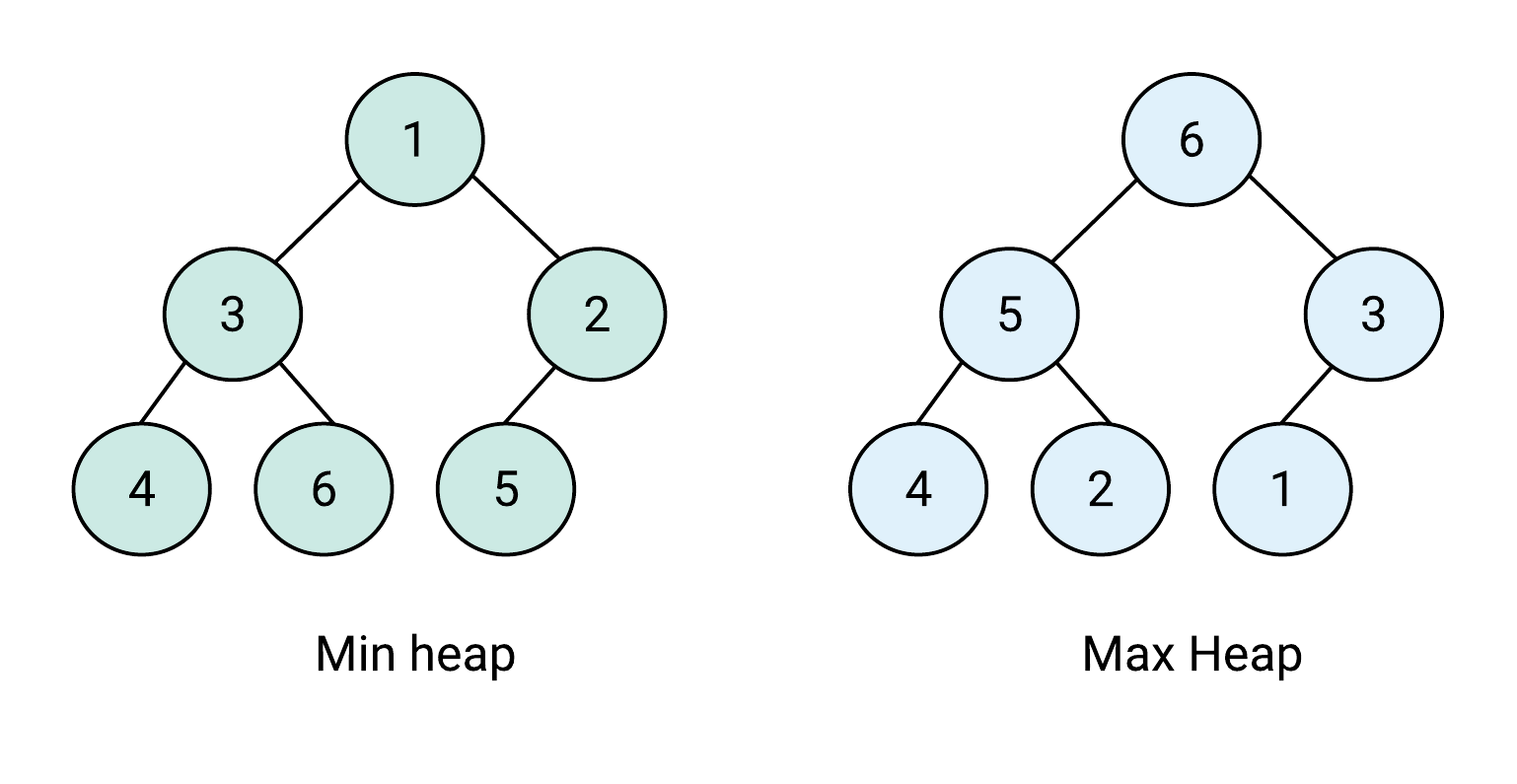
- 모양이
완전 이진트리여야 하고, - 부모가 자식보다 크거나 작다는 규칙을 지킨다.
모양이 완전 이진트리 이기 때문에, 배열로 힙을 구현할 때
- 부모 인덱스의 * 2 = 왼쪽 자식 인덱스
- 부모 인덱스의 * 2 + 1 = 오른쪽 자식 인덱스
- 자식인덱스 // 2 = 부모 인덱스
와 같은 규칙이 적용가능하고, 우리가 힙을 사용하는 이유인 '최솟값 또는 최댓값을 빠르게 구한다' 를 위한 push 혹은 pop operation이 가능해진다.
예를 들어 위 그림의 Min heap에서 0이 push 된다면 먼저 완전 이진트리의 모양을 유지하기 위해 2의 오른쪽 자식으로 붙여주게 된다. 이후 자식노드와의 대소관계를 비교하며 자리를 바꾸면서 원래 있어야 할 자리로 이동시켜준다.
요런 특이한? 방식의 정렬을 통해 힙은 원소가 들어오거나(push) 나갈때(pop) logn의 시간복잡도로 크고 작은 값을 결정지을 수 있게 되고, 따라서 최댓값 혹은 최솟값을 구하기 위해 매번 정렬하여 nlogn의 시간복잡도를 갖는 파이썬의 sort()를 대신하여 더 빠르게 최대/최소 값을 얻어낼 수 있다.
힙은 우선순위로 정렬된 큐와도 같은 역할을 수행하기 때문에 우선순위 큐와 같다고(?) 보면 될 수 있다. 개인적 소견으로는 최대/최소는 힙을 사용하고 다른 더 복잡한 우선순위를 고려해야 하는 경우에는 우선순위 큐 라는 이름의 것을 사용하는 것이 맞지 않을까 생각해본다.
파이썬에서 힙을 사용해 여러가지 문제를 해결해보자.
먼저 개져은 블로그의 글을 하나 첨부합니다..
https://www.daleseo.com/python-heapq/
파이썬에서는 heapq 라는 이름으로 최소힙(min heap)을 제공합니다.
import heapq
heap = []
// heappush 라는 이름으로 원소를 힙에 추가할 수 있고,
heapq.heappush(heap, 4)
heapq.heappush(heap, 1)
heapq.heappush(heap, 7)
heapq.heappush(heap, 3)
# 원소들이 힙에 추가됨과 동시에 정렬되었음을 알 수 있습니다 (상위노드가 하위노드보다 작은/큰 값을 가짐)
print(heap) # [1,3,7,4]
// heappop 이라는 이름으로 원소를 힙에서 제거할 수 있습니다. 마찬가지로 제거할 때 원소들이 정렬되어 부모-자식간의 대소관계를 유지합니다.
print(heapq.heappop(heap))
print(heap) # [3,4,7]
최대힙은 꼼수?를 써서 구현해야합니다..
my_list = [10,5,8,2]
heap = []
for i in my_list:
heapq.heappush(heap, (-i, i))
print(heap)
