오늘은 자료구조 중 트라이에 대해 공부해보자
Trie, 트라이란?
트라이의 용도는 매우 한정적이고 명확하다.
트라이는 문자열을 빠르게 탐색하게 해주는 자료구조로써 문자열 집합을 표현하고 관리하는 방법 중 하나이다.
평범한 트리 구조에서 원하는 요소를 찾는데 걸리는 시간은 O(logN) 이다. 문자열의 경우 문자열의 모든 문자를 확인해야 하므로 M 길이의 문자열을 찾는데에 O(MlogN) 의 시간이 필요할 것이다.
이러한 경우를 위해 특별히 문자열을 관리하고 찾아야 하는 경우 트라이 구조를 사용한다!
Trie 구조
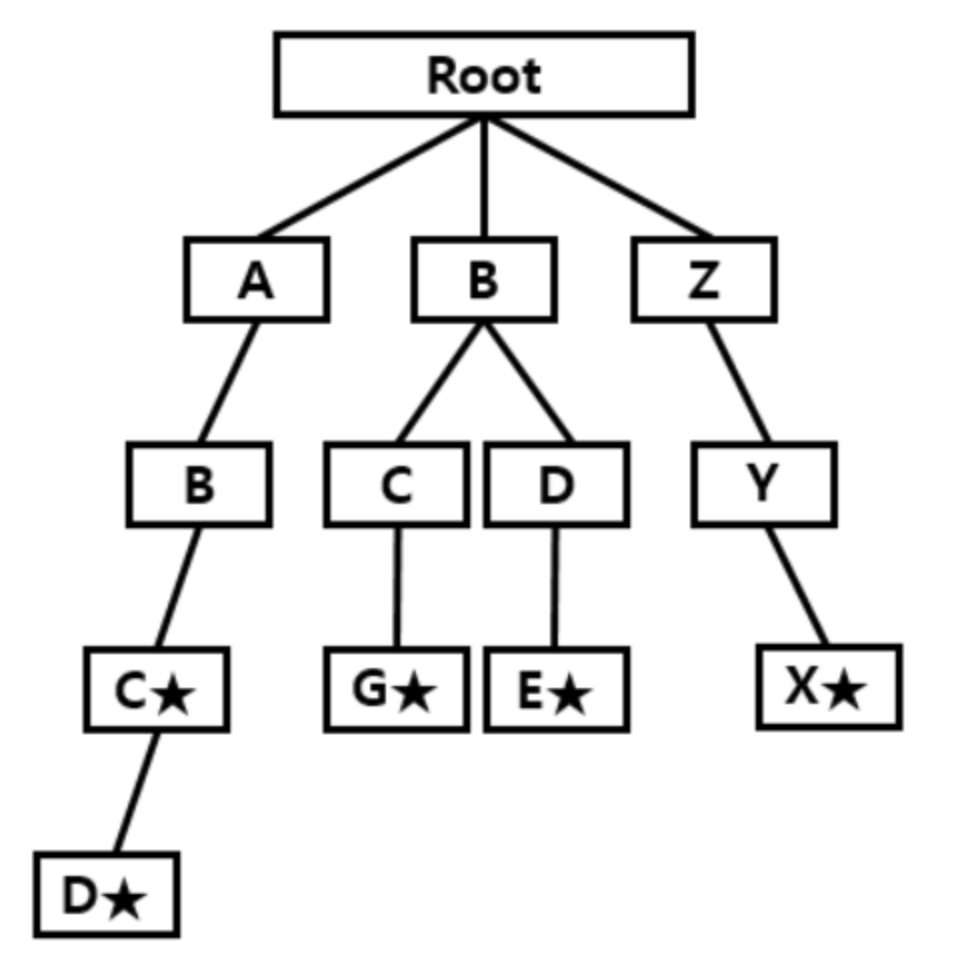
위 그림은 5개의 문자열 [ ABC , ABCD , BCG , ZYX ,BDE ] 가 트라이 구조에 삽입된 형태이다.
트라이 작동 방식은
- 주어진 문자열에서 현재 문자를 가져온 뒤
- 현재 문자로 이루어진 노드가 존재한다면 해당 노드를 통해 다음 문자열을 탐색하고 존재하지 않는다면 현재 문자를 데이터로 갖는 새로운 노드를 할당 받은 뒤 다음 문자를 탐색한다.
- 문자열의 마지막 문자까지 과정을 반복한다.
글로는 아마 이해가 잘 안될 것이다.
첫번째 문자열 ABC 를 트라이에 삽입한 뒤 두번째 문자열 ABCD 를 삽입하려는 상황을 생각해보자.
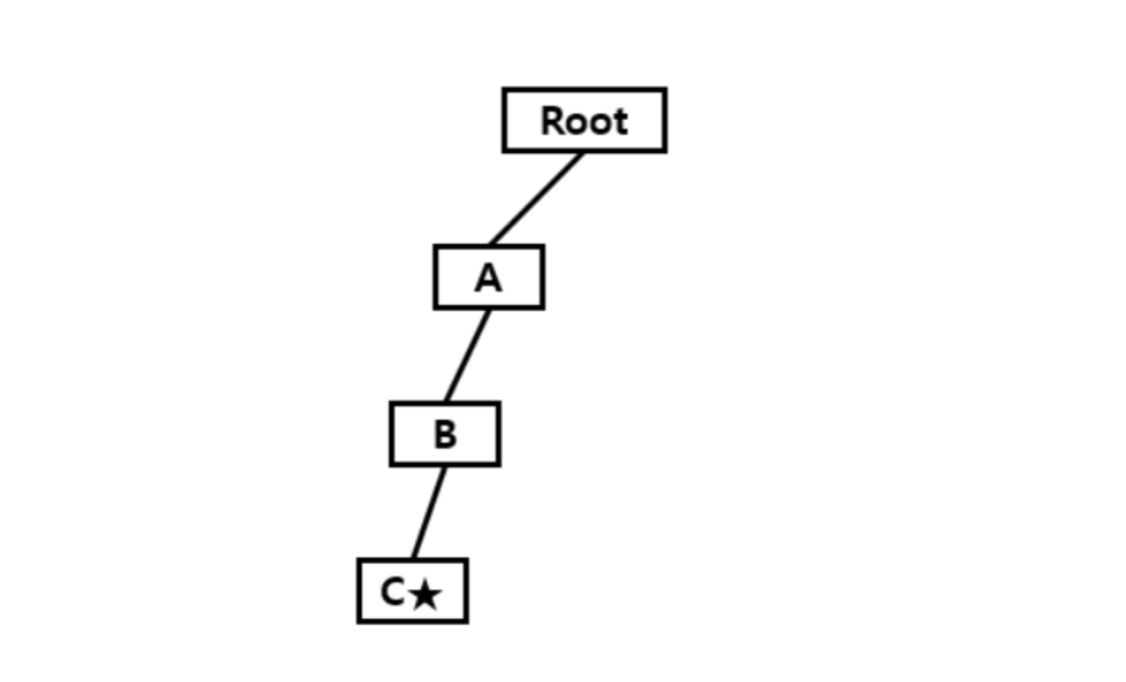
A,B,C 가 차례대로 새로운 노드를 통해 생성되고 문자열의 끝인 C에 표시가 되어있는 상태이다.
이제 두번째 문자열 ABCD 를 보면,
- 루트노드에서 첫번째 문자인 A 노드가 존재하는가? 존재한다!
- A 를 통해 다음 문자인 B를 확인해보자
- A 노드에 B 노드가 존재 하는가? 존재한다!
- B 노드에 다음 문자인 C 노드가 존재하는가? 존재한다!
- C 노드에 다음 문자인 D 노드가 존재하는가? 존재하지 않는다!
- C 노드에 D 노드를 새롭게 생성해 달아주고
- D 는 문자열의 마지막 문자라는 표시를 함께 해준다.
그럼 아래와 같은 상태가 될 것이다.

같은 과정을 반복해서 문자열을 삽입하면,
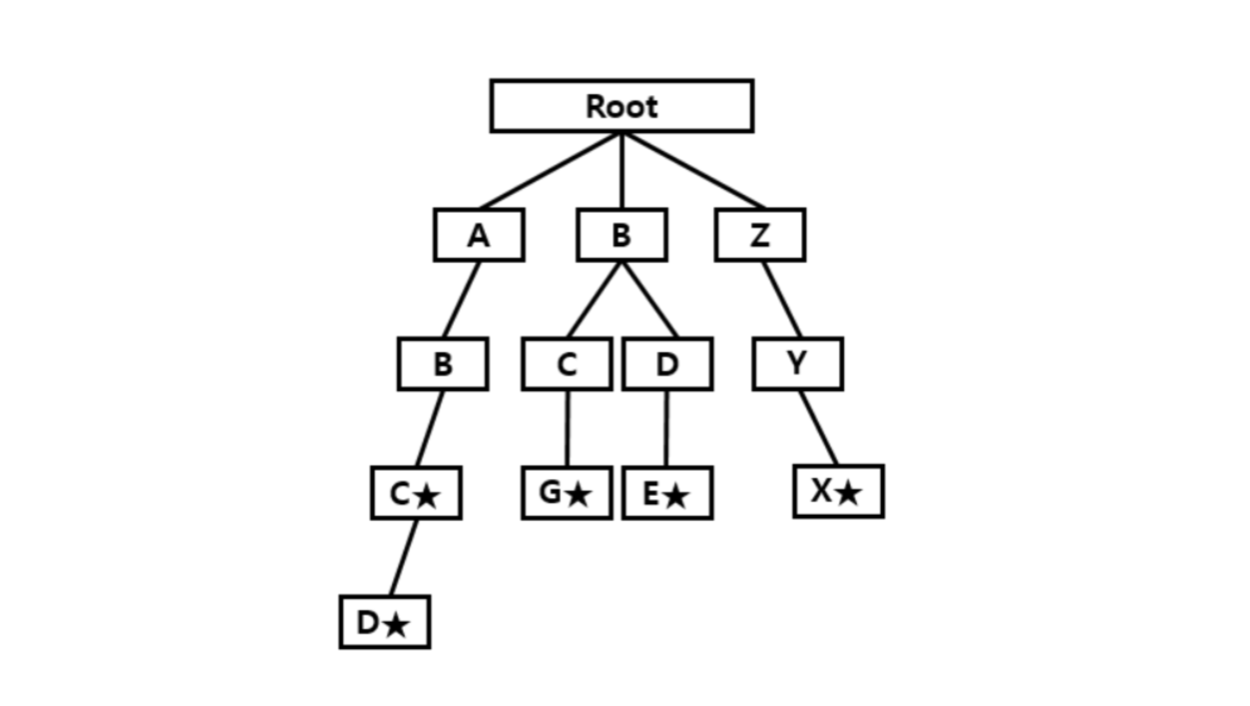
이와 같은 형태를 갖는 트라이 구조가 완성된다.
Trie, 트라이의 특징
이런식으로 동작하는 트라이는
- 집합에 포함된 문자열의 접두사들에 대응되는 노드들이 서로 연결된 형태를 띄게 된다.
- 루트에서부터 내려가는 경로에서 만나는 글자들을 모으면 찾고자 하는 문자열의 접두사를 얻게된다.
장점
트라이는 문자열을 빠르게 찾을 수 있고, 문자열을 새롭게 추가시 문자열의 길이만큼 노드를 따라가거나 추가하면 되기 때문에 길이 M 의 문자열을 탐색할때는 O(M) 만큼의 시간이 필요하게 된다.
일반적인 트리에서 O(MlogN) 의 시간이 걸리는 것에 비해 확연히 빠른 속도이다.
단점
하지만 트라이 구조의 결정적인 단점은 메모리이다.
메모리 소비가 괸장히 크다. 모두 소문자 혹은 대문자라고 가정해도 모든 노드는 자식 노드를 가리키는 26개의 포인터를 가져야 하기 때문이다.
최악의 경우라면 트라이 구조를 사용하는데 필요한 메모리는 포인터 크기 * 포인터 배열 개수 * 총 노드의 개수 만큼이다.
루트노드에 26개의 자식노드, 26개의 자식 노드에 또다시 26개의 자식 노드.... 라고만 생각해봐도 메모리 소비가 굉장히 크다는 단점이 존재한다.
