첫 번째 항부터 마지막 항까지 일정한 수(공비)를 곱하여 만들어진 수열을 "등비 수열"이라고 한다.
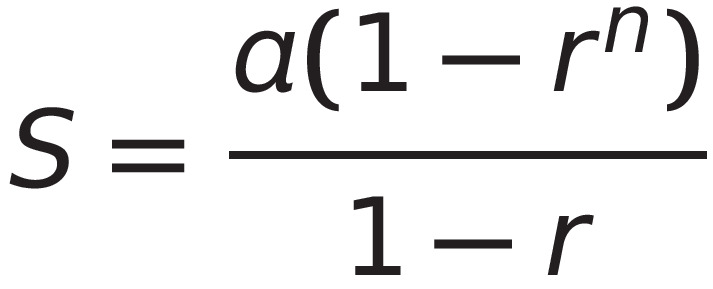
a:첫번쨰 항
r:공비(단, r!=1)
n:항의 갯수
다음 수열 1,2,4,8,16(수열의 원소가 x2씩 되고 있음)의 합을 구한다고 하면
r=2, a=1, n=5이므로
1(1-2^5)/(1-2)=31
이렇게 모든항의 합을 구할 수 있다.
r=1인 경우는
Sn=an이다.
예시) 2 + 2 + 2 + 2= 2 x 5=10
등차수열과 헷갈릴 때 참고하기
등차수열
1,2,3,4,5(d=1)
2,5,8,11,14(d=3)
2,7,12,17,22(d=5)
수열의 원소가 +d씩 된다.
등비수열
2,2,2,2,2(r:1)
2,4,8,16,31(r:2)
3,6,9,27,81(r:3)
수열의 원소가 x r씩 된다.
