본 블로그의 모든 글은 직접 공부하고 남기는 기록입니다.
잘못된 내용이나 오류가 있다면 언제든지 댓글 남겨주세요.
라그랑주 승수법 Lagrange Multiplier
라그랑주 승수법은 제약 조건이 있는 다변수 함수의 최적화 문제를 제약 조건이 없는 형태로 바꾸어 푸는 방법입니다. 왜 그렇게 하냐면 일반적으로 제약 조건을 포함하는 형태로 직접 방정식을 구하려면 매우 번거롭기 때문입니다.
다변수함수가 열린 공간에서 정의될 경우, 주어진 함수의 극점에서는 그래디언트가 0이 됩니다. 따라서 인 지점을 구하면 극점을 찾을 수 있습니다. 문제는 제약 조건으로 인해 함수 공간이 한정되는 경우입니다. 예시를 보겠습니다.
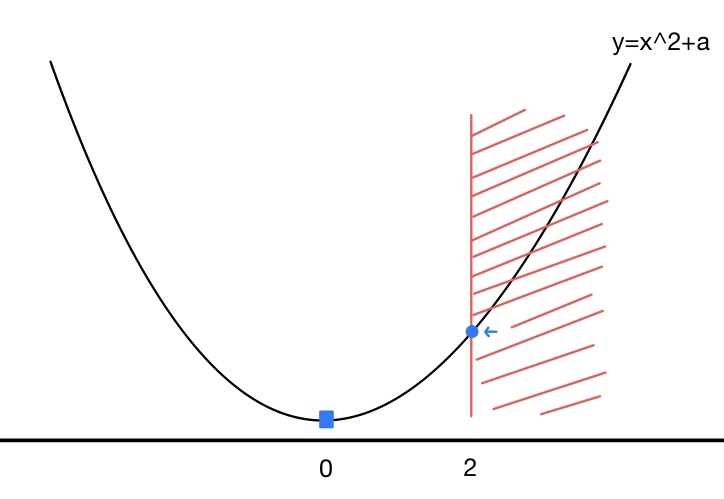
위 그림에서 원래 극소점은 파란색 네모 부분입니다. 그런데 만약 제약 조건에 의해 함수의 정의역이 빨간색 빗금친 구간으로 한정된다면 어떻게 될까요? 극소점이 파란색 점으로 바뀌겠죠.
물론 이 그림과 같은 경우는 상대적으로 계산하기 쉽습니다. 그런데 이런 2차원 함수가 아니라, 같은 10차원 함수가 주어진다면 어떨까요? 또, 여기에 3차원 람보르기니 모양의 제약 조건이 주어진다면 어떨까요? 생각만 해도 골치가 아픕니다.
핵심 아이디어
라그랑주 승수법의 핵심 아이디어는 주어진 함수 , 제약 조건 에 대해 가 들의 선형 결합으로 표현 가능하다는 것입니다. 즉, 제약 조건에 의해 한정되는 함수 공간을 매번 구하는 대신 를 일종의 기저처럼 취급해서 를 나타낼 수 있습니다.
라그랑주 승수법은 그 특성상 주어진 함수와 제약 조건의 접점에 집중합니다. 왜냐하면 두 함수의 접점이 우리가 풀고자 하는 함수 공간의 경계가 되고, 많은 경우 이곳에 위치한 극점에서 우리가 찾고 있는 최댓값 또는 최솟값을 얻을 수 있기 때문입니다.
반드시 최댓값 또는 최솟값이 존재하는 건 아니라는 점을 주의해야 합니다.
제약 조건이 등식이라면...

위 그림에서 는 두 함수가 접할 때 최댓값을 갖습니다. 또, 접점에서는 제약 조건과 주어진 함수가 같은 값을 갖습니다.
그런데 두 함수의 접점에서는 각각의 그래디언트가 평행하므로, 다음이 성립합니다.
이 때 를 라그랑주 승수라고 합니다. 는 임의의 상수이므로 다음과 같이 쓸 수 있습니다.
라그랑주 승수법에서 제약 조건이 등식으로 주어지면 앞에 +가 붙든 -가 붙든 상관 없는 이유가 바로 이것입니다. 어차피 그래디언트의 크기가 0이므로 방향이 어느 쪽이든 문제가 되지 않기 때문입니다.
한 가지 중요한 조건은 이어야 한다는 것입니다. 만약 이라면 원 함수와 동일한 해를 갖게 됩니다. 즉, 제약 조건이 해에 전혀 영향을 주지 못합니다.
제약 조건이 부등식이라면...
반대로, 제약 조건이 부등식으로 주어진다면 그래디언트의 방향이 중요해지므로 앞에 붙는 기호를 주의해야 합니다. 왜냐하면 라그랑주 승수값에 따라 제약 조건이 의미가 있을 수도 있고 없을 수도 있기 때문입니다.

위 그림에서 제약 조건을 대신 로 바꾸어 보겠습니다. 접점에서 두 그래디언트는 여전히 평행하고, 는 임의의 상수입니다.
극점에서 그래디언트가 0이므로, 는 그래디언트가 작아지는 방향으로 움직여야 최적점을 찾을 수 있습니다.
편의상 식 (1)을 다음과 같이 표현하겠습니다.
식 (2)의 의미에 대해 곰곰이 생각해보겠습니다. 우리는 현재 를 최적화하고 싶습니다. 그러므로 의 최소값은 0입니다. 따라서 이어야 합니다. 다시 말해 이거나 이어야 합니다. 아니면 둘 다 0일 수도 있겠죠.
제약 조건의 그래디언트가 0인 경우
라면 제약 조건을 항상 만족하므로, 식 (2)는 아래와 같이 바꿔 쓸 수 있습니다.
따라서 만 최적화하면 됩니다.
라그랑주 승수가 0인 경우
이라는 것은 를 의 선형결합으로 나타낼 수 없다는 것을 의미합니다. 즉, 두 그래디언트가 평행하지 않습니다. 따라서 그래디언트의 방향에 따라 제약 조건을 만족하거나 만족하지 않습니다.
이럴 때는 인 경우와 인 경우를 모두 따져봐야 합니다. 왜냐하면 문제의 목적과 조건에 따라 어떤 방향이 제약 조건을 만족하는지가 바뀌기 때문입니다.
KKT 조건
한 편, 위 두 가지 경우에서 모두 만족해야 하는 숨은 조건이 있습니다. 바로 입니다. 이어야 를 의 선형결합으로 나타낼 수 있는지 없는지를 판정할 수 있습니다.
만약 일 경우, 와 가 평행하지만 그 방향은 반대라는 뜻이 됩니다. 이는 곧 두 함수의 최적점이 서로 반대 방향에 위치한다는 것이므로, 제약 조건을 만족할 수 없습니다.
- 는 모든 에 대해 미분가능할 것
지금까지 살펴본 위 3가지 조건을 KKT(쿤 크루쉬 터커) 조건이라고 합니다.
참고문헌
