최근 효율적인 트랜스포머 모델 학습 방법으로 사용되고 있는 MoE (Mixtures of Experts)의 기반이 되는 논문 중 하나로, 개념적인 부분까지만 해석 및 정리해보았습니다.

원본 링크

---

Adaptive Mixtures of Local Experts (1991)

Abstract

우리는 (전체 훈련셋을 여러 셋으로 나누어 각 일부를 학습하도록 다루는) 다수의 분산 네트워크들로 구성된 시스템에 대한 새로운 지도 학습 절차를 제안한다. 이를 통해서 vowel discrimination task[^1] 를 적절한 하위 task로 나누고, 각 task가 아주 단순한 전문가 네트워크 (expert network)를 통해 해결될 수 있음을 보일것이다.

아래 설명에서 vowel discrimination task에 대한 적용 과정 부분은 생략

Making Associative learning Competitive

만약 역전파를 사용해, 하나의 다층 네트워크에 대해서 서로 다른 원인(occasion)에 따라 서로 다른 subtask들을 수행하도록 학습한다면, 강한 간섭(interference)으로 인한 느린 학습 속도와 좋지 않은 일반화(generalization) 성능을 나타낼 것이다. 하지만 훈련셋이 명확한 subtask로 자연스럽게 나누어질 수 있는 경우라면, 서로 다른 "전문가(expert)" 네트워크와 게이팅 네트워크(gating network)[^2]로 구성된 하나의 시스템을 사용해 간섭 효과를 낮출 수 있다.

Hampshire와 Waibel(1989) 연구에서는 훈련에 앞서 subtask로 나눌 수 있다면 이러한 시스템이 사용 가능하다는 점을 설명했고, Jacobs(1990) 연구에서는 어떻게 case들을 적절한 전문가에 할당할 수 있을지를 학습하는 관련 시스템에 대해 설명했다.

이와 같은 시스템의 숨은 아이디어는 게이팅 네트워크가 새로운 case를 하나 또는 일부 전문가 네트워크에 할당하고, 출력이 올바르지 않다면 (게이팅 네트워크와) 해당되는 전문가의 가중치 값을 조절한다는 점이다. 이렇게하면 (아주 미묘한 차이를 나타내는) 서로 다른 전문가들 사이의 가중치에 대한 간섭을 줄일 수 있다(decoupling). 또한 입력 벡터 공간에서 협소한 지역에 대해서만 각 전문가들이 할당된다는 지역적인 특성도 표현할 수 있다.

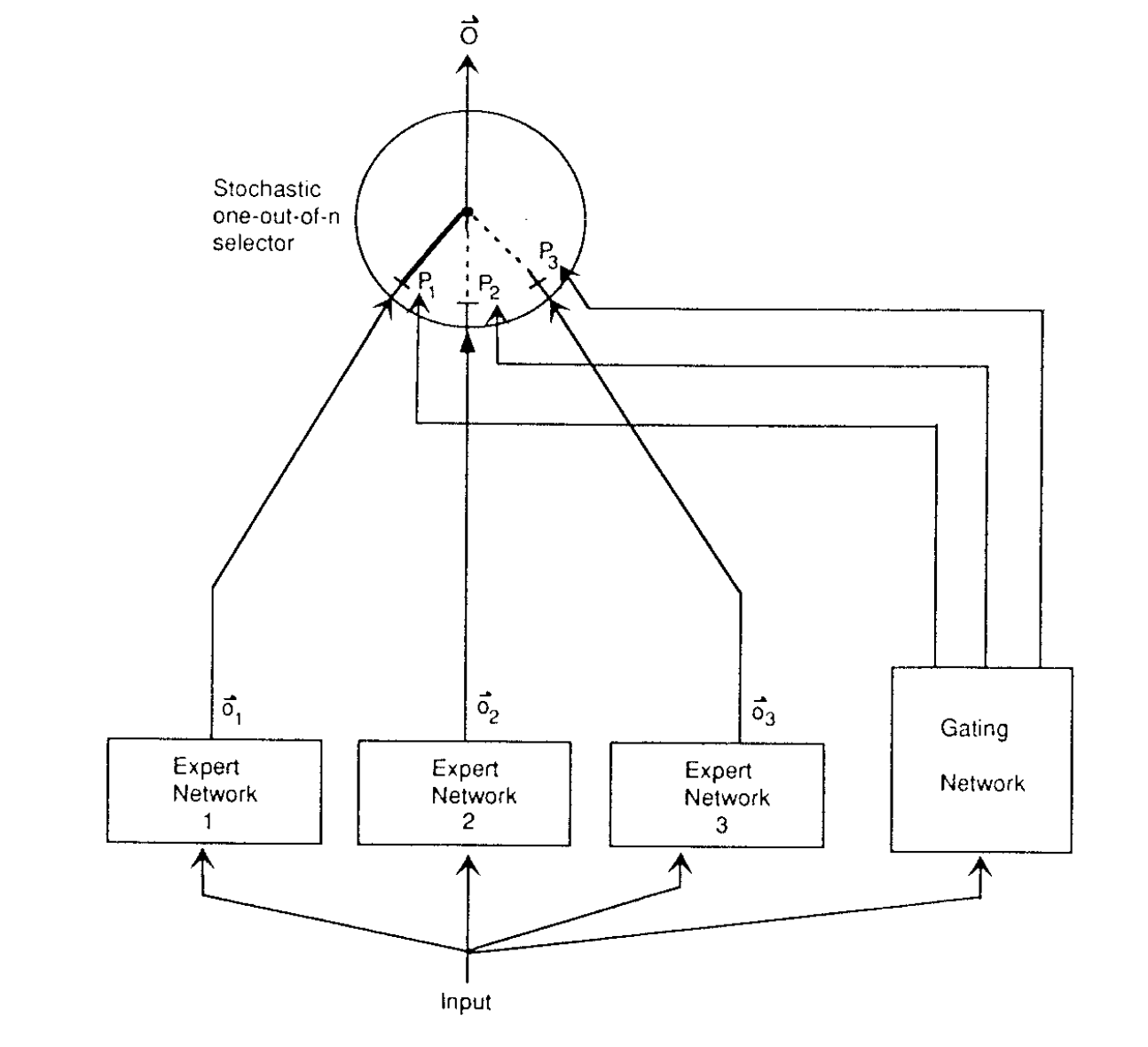A system of expert and gating networks

하지만 앞선 연구들에서는 지역화(localization)가 제대로 반영되지 않은 오류 함수(error function)를 사용하였다. 전체 시스템의 최종 출력을 지역 전문가들의 출력의 선형 조합으로 보았고, 게이팅 네트워크는 이런 선형 조합에서 각 지역적인 출력의 일부만 결정한다고 추정했다. 즉 c라는 case에 대한 최종 오류는 다음과 같이 나타낼 수 있다.

• o = 케이스 c에 대한 전문가 i의 출력 벡터

• p = 결합된 출력 벡터에서 전문가 i의 부분적인 기여도

• d = 케이스 c에 대한 기대 출력값

  이때 오류는 기대 출력값과 각 지역 전문가들의 출력이 섞인 값의 차이로 계산되며, 따라서 오류를 줄이기 위해서는 각 지역 전문가들의 출력이 결합되면서 발생한 잔차 오류(residual error)를 상쇄시켜야한다. 하지만 어떤 전문가의 가중치 값이 변경된다면 잔차 오류에도 영향을 미치게되는 강한 커플링 관계를 가지면서, 각 케이스를 처리할 때 (적합한 하나의 전문가가 아닌) 여러 전문가를 사용하게 되는 특성을 나타낸다. 이는 오직 하나의 전문가만 사용되는 솔루션이 선택될 수 있도록 목적함수의 패널티 조건을 추가하는 방법으로 보정할 수 있으나, 이렇게되면 여러 전문가들이 협력하기보다는 다른 전문가가 사용될 수 없도록 억압(compete)하는 방식으로 볼 수 있다.
  우리는 앞서 각 전문가들의 출력을 선형적으로 조합하는 대신, 게이팅 네트워크가 각 경우(occasion)마다 단일 전문가가 사용되도록하는 확률론적 결정을 사용한 오류 함수를 만들어보았다.

  $E^c = <||d^c - o^c_i||^2> = \sum_i p^c_i ||d^c - o^c_i ||^2$

  앞서 제시한 새로운 오류 함수에서는 각 전문가가 출력 벡터의 잔차 보다는 전체를 출력해야한다는 점을 명심하자. 결과적으로 특정 훈련 케이스가 주어졌을 때 각 지역(local) 전문가의 최종 목표는, 주변 다른 전문가의 가중치로부터 직접적인 영향을 받지 않도록 하는 것이다. 그럼에도 어떠한 전문가가 그 가중치를 변경했을 때에는 게이팅 네트워크가 해당 전문가에 대한 책임(Responsibility)을 수정하는 간접적인 커플링이 여전히 존재하지만, 이러한 책임이 지역 전문가가 남기는 오류 흔적 자체에 영향을 주는 것은 아니다.

  만약 게이팅 네트워크와 지역 전문가 모두 새로운 오류 함수를 사용한 경사하강법으로 학습을 수행한다면, 해당 시스템은 각 훈련셋에 대해 단일 전문가에게만 기여하는 경향을 보일 것이다. 하나의 전문가가 모든 전문가의 평균 오류 가중치보다 낮을 때는 게이팅 네트워크의 출력에 있어 해당 전문가의 책임도가 커지고, 반대로 모든 전문가의 가중치 평균보다 더 나쁘다면 해당 전문가의 책임도가 감소한다.

  앞선 오류 함수가 실제에서 잘 동작하지만, 시험(simulation)에서는 보다 나은 성능을 나타내는 다음 오류 함수를 사용하였다.

해당 오류 함수는 혼합된 가우시안 모델을 사용하여 출력 벡터를 생성하는 음의 로그 확률 함수이다. 이는 앞선 오류 함수를 출력에 대해 편미분한 함수로부터 유도된 것이다. 이때 케이스 c에 대한 전문가 i의 부분적인 기여도인 기존 p 대신 전체 전문가 기여도에 대한 전문가 i의 기여도 비율로 대신하여 해당 전문가의 관계성 측정을 반영하였다.

Making Competitive Learning Associative

경쟁식 네트워크(competitive network)에서의 데이터 벡터는, 입력 벡터를 출력 벡터롤 맵핑하는 하나의 관계형 네트워크(associative network)에서의 입력 벡터들과 동일한 역할을 수행하는 방법으로 학습된다. 이러한 대응점(correspondence)은 관계형 네트워크에서 전처리 방식으로 경쟁식 학습을 사용하는 모델로 가정하는 경우로 가정한다. 한 가지 다른 관점이라면, 경쟁 학습에 사용된 데이터 벡터들이 관계형 네트워크의 출력 벡터들과 대응한다는 부분이다. 경쟁 네트워크는 출력 벡터들의 (입력이 없는) 확률론적 생성자라고 볼 수 있으며, 경쟁 학습은 데이터 벡터의 분포와 일치(match)하는 분포를 가지는 출력 벡터를 생성해내는 네트워크를 만들기위한 절차로 볼 수 있다.

각각의 경쟁 은닉층(competitive hidden unit)의 가중치 벡터는 다차원 가우시안 분포의 평균(mean)을 나타내고, 출력 벡터들은 처음 선택된 하나의 은닉층으로부터 생성되며, 이후 출력 벡터는 선택된 은닉층의 가중치 벡터에 의해서 결정된 가우시안 분포로부터 하나를 선택한다. 특정한 경우의 어떤 출력 벡터 o를 생성하는 로그 확률은 다음과 같다.

• i = 전체 은닉층에서의 인덱스
• u = 은닉층에서의 가중치 벡터
• k = 정규화(normalizing) 상수
• p = 은닉층 i가 선택될 확률 (=mixing proportions)

"Soft" 경쟁 학습은 훈련셋에서 출력 벡터들을 생성해내는 확률들의 곱을 증가시키기 위해 해당 가중치(variances, mixing proportions)를 변경한다. "Hard" 경쟁 학습은 일부 다른 은닉층에의해 생성될 수 있는 데이터 벡터의 가능성을 무시하고 "Soft" 경쟁 학습을 진행한 경우에 대한 하나의 단순한 근사치이다. 대신, 가장 근사한(closest) 가중치 벡터를 가지는 은닉층으로부터 생성된다고 가정하므로, 해당 가중치 벡터만 변경하면 데이터 벡터 생성 확률을 높일 수 있다.

만약 하나의 경쟁 네트워크가 출력 벡터들을 생성한다는 관점에서 본다면, 입력 벡터가 어떤 역할을 수행해야하는지 명확하지 않다. 하지만 경쟁 학습은 Barto[^3]와 동일한 방식으로 일반화(generalized) 될 수 있다. 경쟁 네트워크에서 각 은닉층은, 다차원 가우시안 분포의 방법으로 구체화하는 출력 벡터를 가지는 전체 전문가 네트워크로 교체할 수 있다. 따라서 해당 방법(means)들은 현재 입력 벡터에 대한 하나의 기능이 되고, 가중치(weights)보다는 활성화 수준(activity levels)으로 표현될 수 있다.

추가로 우리는 입력 벡터에 따라 전문가의 혼합 비율이 결정될 수 있도록 하는 게이팅 네트워크를 사용한다. 이는 이전의 오류 방정식을 사용해 지역 전문가들 간에 경쟁할 수 있는 시스템을 제공한다.

또한 우리는 입력 벡터가, 각 전문가 네트워크에 의해 결정된 분포에 대해서, 동적으로 공분산 행렬(covariance matrix)을 결정하는 매커니즘에 대해 소개한다. (가능성에 대해서는 검증되지 않음)

(이어지는 내용으로 Vowel Recognition task에 대한 검증 과정이 있으나, 본 설명에서는 제외하였다.)

주석

[^1]: 서로 다른 단어들의 소리를 구별하는 능력
[^2]: 각 훈련 케이스에 대해서 어떤 전문가 네트워크가 사용되는 것이 좋을지 결정하는 기능 수행
[^3]: 하나의 입력 벡터를 추가한 일반화된 학습 오토마타로, 오토마톤의 동작이 입력 벡터에 대한 조건부가 될 수 있다.