Bits and Number

노정훈·2023년 3월 26일
ComplementIEEE754bitcodenumber
0

CE

목록 보기
5/24

Numeral System

  • Base-? System or Radix-? System 이라고 불림. ?는 base에 해당하는 수
  • 같은 digit(숫자기호)라도 어느 자리에 있느냐에 따라 크기가 다르며 해당 자리에 따라 다른 크기는 base에 의해 결정.

Base R System

  • R은 base를 의미하며 다음과 같이 표기
Abase=AR=an−1an−2...a1a0a−1a−2...a−mA_{base} = A_R = a_{n-1}a_{n-2}...a_1a_0a_{-1}a_{-2}...a_{-m}
  • 위의 value는 다음과 같음.
V(Abase)=V(AR)=∑i=−mn−1aiRiV(A_{base}) = V(A_R) = \displaystyle\sum_{i=-m}^{n-1}{a_iR^i}
  • 주로 사용되는 system에는 Decimal system, Hexadecimal system, Octal System, Binary System이 있음.

Positive Integer Representation

  • Computer에서는 대부분 Binary system을 이용하여 positive integer를 표현
  • 이외에도 Binary Coded Decimal(BCD)와 같은 base-10 기반으로 숫자를 bit로 표현하는 방식도 있지만 실제 컴퓨터 내부 연산에서는 사용하지 않음.

Positive integer representation in programming language

  • C language 등에서 unsigned 키워드가 붙은 경우 positive 만을 표현
  • unsigned char : 8bits, 1byte
  • unsigned short(int) : 16bits, 2bytes
  • unsigned long(int) : 32bits, 4bytes
  • unsigned int : 32bits, 4bytes
  • unsigned long long(int) : 64bits, 8bytes

Negative number

  • Computer에서 negative number를 표현하는 방법은 크게 3가지가 있음.

    1. Sign and Magnitude
    2. 1's Complement
    3. 2's Complement

Sign and Magnitude

  • 가장 simple
  • MSB가 sign을 나타내고 나머지 bit들은 positive integer와 마찬가지로 magnitude를 나타냄.
  • 단점으로 +0과 -0의 표현이 각각 존재하게 됨. 또한 logic operation과 arithmetic operation을 구현하기 쉽지 않음.

1's complement

  • positive integer 표현에서 모든 bit에 NOT연산을 취함으로서 대응되는 negative integer를 구하는 방법

    Ex. 011(=+3)에 NOT연산을 취하면 100이 되고 이를 -3으로 삼는다.

  • +0과 -0에 대한 표현이 각각 존재한다.

2's complement

  • negative integer를 구할 때 1's complement를 구한 후 1을 더해준다.

    Ex. 011(=+3)의 1's complement인 100에 1을 더한 101이 -3의 표현형이 됨.

  • zero에 대한 표현형이 하나가 되며 arithmetic operation을 구하기도 간단해 현재 가장 널리 사용되는 방식.

Subtraction using Complement

  • 1's complement와 2's complement는 덧셈만으로 뺄셈 구현 가능
  • MSB에서 carry out(=End around carry)가 발생할 경우, 1's complement는 해당 MSB에서 carry out을 LSB에 더해주면 되고, 2's complement는 해당 MSB에서 carry out을 그냥 빼줌.

Example 1

DecimalSign and Magnitude1's complement2's complement
5000001010000010100000101
-8100010001111011111111000
result
-3100000111111110011111101

Example2

DecimalSign and Magnitude1's complement2's complement
8000010000000100000001000
-5100001011111101011111011
MSB carry out100000010100000011
result
3000000110000001100000011
  • Example 1의 경우 MSB carry out이 없는 경우로 complement를 사용할 때 그냥 더해주면 됨.
  • Example 2의 경우 MSB에서 carry out이 발생한 경우로 위의 설명대로 계산해주면 됨.
  • Sign and Magnitude 방식은 그냥 더해서는 안되므로 뺄셈을 위한 별도의 처리기가 필요

Overflow Detection for 2's complement

  • MSB에서 carry in, carry out이 다를 경우 overflow
  • carry in : 이전 자리의 연산 결과로 carry가 넘어온 것
  • carry out : 현재 자리의 연산 결과로 carry가 발생한 것

Example

No overflowNo overflowoverflowoverflow
(carry) 110000000(carry) 001111000(carry) 010000000(carry) 101111100
(+65) 01000001(-65) 10111111(+65) 01000001(-65) 10111111
(-44) 11010100(+44) 00101100(+90) 01011010(-90) 10100110
result
(+21) 00010101(-21) 11101011(-101) 10011011(+101) 01100101
  • 위 Example에서 왼쪽 2개의 경우 overflow가 발생하지 않아 정확한 결과가 나옴.
  • 오른쪽 2개의 경우는 overflow가 발생함.

Overflow and Underflow

Overflow

  • 처리 가능한 범위를 넘어서는 연산 결과가 발생한 경우
  • Computer에서 overflow 발생 시 condition code registor(CCR)의 overflow에 해당하는 bit가 '1'로 설정.
  • MSB에서 발생한 carry 값이 overflow bit

Underflow

  • 처리가능한 범위보다 작은 연산 결과가 발생하는 경우

Real Number

  • 실수를 bit로 표현하는 방법을 알기 이전에 소수를 2진수로 표현할 수 있어야 함.

<소수의 2진수 표현>
1. 10진수의 소수값에 2를 곱함.
2. 2를 곱한 결과가 1 미만이면 0을 기록, 1 초과할 경우 1을 기록하고 결과값에서 1을 뺌.
3. 위 과정들을 반복하며 결과값이 1이 나온 경우 1을 기록하고 변환을 끝냄.

Example

0.50.
0.5 x 2 = 1.01

∴(0.5)10=(0.1)2∴(0.5)_{10} = (0.1)_2

  • 실수의 2진수 표현을 bit로 표현하는 방법은 크게 Fixed-point Representation과 Floating-point Representation이 있다.

  • Fixed-point Representation : 기존의 integer를 표현하던 방식 그대로 사용

  • Floating-point Representation : 소수점의 위치가 고정되지 않고 변경됨. Scientific Notation에 기반.

    cf) Scientific Notation
    x×10y=xEyx × 10^y = x Ey

    • 1≤x＜101≤x＜10
    • y는 0이 아닌 integer

  • 일반적인 computer에서는 Float-point representation이 사용되며 일부 DSP(Digital Signal Processing) system에서만 fixed-point representation이 사용됨.

  • Fixed-point representation는 동일한 크기의 bit로 표현할 수 있는 수의 range가 Floating-point representation에 비해 너무나 작음.

Floating-Point Representation

  • 소수점이 고정되지 않지만, 고정된 유효숫자 자리수를 가지기 때문에 큰 수를 표현할 때 정밀도가 떨어지고 아주 작은 수를 표현하여 정밀하게 사용될 때는 나타낼 수 있는 수의 크기가 작아짐.
  • 줄여서 float라고 부름.
  • Floating-point representation을 제한된 크기의 bit로 나타내는 방법은 IEEE 754로 표준화 되어 있음.

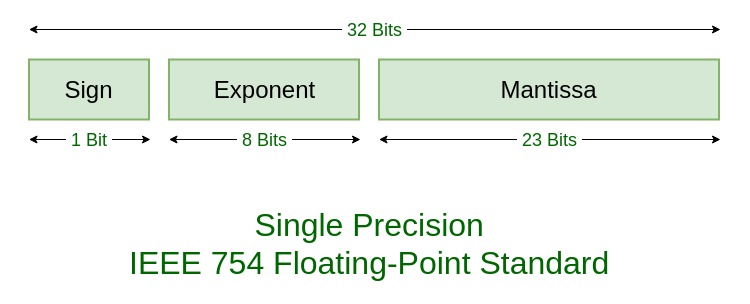
IEEE 754

  • 지수(exponent)부와 가수(mantissa or fraction)부로 나누어 표기
  • Base : 몇 진수인지 나타냄.
  • Exponent : 수치의 크기 결정
  • Mantissa : 표현가능한 유효 숫자. precision을 결정.

    Example in Decimal
    (123456000)10(123456000)_{10} => 123456×103123456 × 10^3 => 1.23456×1081.23456 × 10^8

    • 10이 Base
    • 3,8이 exponent
    • 123456, 1.23456이 mantissa

변수형크기 및 정확도사용되는 곳구조(bit)
float(or float32)32bit single precisionmemorys(1)+e(8)+m(23)
double(or float64)64bit double precisionmemorys(1)+e(11)+m(52)
  • GPU 등에서는 float32가 많이 사용되고, CPU에서는 float64가 많이 사용됨.
  • mantissa에 할당된 bit가 많아질수록 정밀도가 향상됨.
  • 0으로 나눈 결과처럼, 숫자가 아닌 결과에 대한 표현(NaN, Not a Number)들도 쉽게 처리 가능.

Example: −13.62510-13.625_{10}를 IEEE 754 single-precision 형식으로 표현.
13.62510=1101.1012=1.101101×2313.625_{10} = 1101.101_2 = 1.101101 × 2^3
S = 1 (-)
E = 00000011(exponent 3) + 01111111(bias 127) = 10000010
M = 10110100000000000000000

  • Sign 은 양수면 0 , 음수면 1
  • Exponent는 exponent 값에 bias 값 127을 더해줌. double-precision인 경우 1023을 더해줌.
  • Mantissa는 Decimal을 Binary로 변환 후 Scientific Notation 형태로 나타낸 후에 소수점 뒤의 숫자를 나타냄. 23bit 크기만큼 0을 채워줌.

Code for Number(Symbol)

Code

  • 일상 생활에서 사용되는 문자나 숫자를 컴퓨터가 인식하기 위해 기호화한 것.
  • Number의 symbol에 초점을 맞춘 것이라고 볼 수 있음.
  • Internal representation : 계산이 효과적으로 이루어지는데 집중.
  • External representation : 숫자를 보여주거나 입력장치로부터 숫자(엄밀하게는 숫자 기호)를 입력받을 때 사용.

BCD(Binary Coded Decimal) System

  • 10진수에서 각 자리 digit을 4bit binary로 변환하여 표현

  • 8-4-2-1 code 라고도 불림.

    Example
    23 => 2 : 0010 , 3 : 0011 로 변환하여 최종적으로 0010 0011로 표시됨.

  • 10진법에서 2진법으로 변환을 가장 쉽게 할 수 있다는 장점.

  • bit의 낭비가 크고 complement를 구현하기 어렵다는 단점 존재.

EBCDI(Extended Binary Coded Decimal Interchange) Code

  • BCD code를 확장하여 8bit로 표현.

  • 상위 4bit가 Zone을 나타내고, 하위 4bit가 BCD를 가리킴.

  • 일반적으로 Zone은 1111 로 표현.

  • sign 부호는 가장 하위자리 Zone으로 표현, + sign은 1100 , - sign은 1101 로 표현.

    Example : +89710+897_{10}

    Zone8Zone9Sign7
    111110001111100111000111

  • 숫자만 사용하는 경우 낭비가 심함.

  • Packed 10진수 방식과 같이 zone을 제거하고 BCD만 사용하는 경우도 있음.

Excess-3 Code

  • BCD code에 +3을 해준 것.
  • 9의 보수를 매우 쉽게 얻을 수 있음.

Gray Code

  • 0에서 9까지 순환적으로 변할 때, 각 과정마다 오직 한 비트씩만 변화함.
  • 입력 도중의 에러나 오차를 쉽게 검출할 수 있으며 변경할 bit가 적다는 장점.
  • BCD code의 인접하는 비트를 XOR 연산하여 만들어진 코드
DecimalBCDExpress-3Gray
0000000110000
1000101000001
2001001010011
3001101100010
4010001110110
5010110000111
6011010010101
7011110100100
8100010111100
9100111001101

Reference:
1) https://dsaint31.me/mkdocs_site/CE
2) https://www.geeksforgeeks.org/ieee-standard-754-floating-point-numbers/
3) https://woo-dev.tistory.com/92

profile
노정훈
노정훈
이전 포스트

Bits and Boolean Algebra

다음 포스트

Bits and Character + Web browser

0개의 댓글