Recursive Subdivision using DFS

subdivide function using pseudo code

function subdivide(x,y,size)
{
	IF size != 1 AND "the pixels in the square are not all the same color"{
    	half = size/2
        subdivide(x,y,half)            # upper left quadrant
        subdivide(x,y+half,half)       # lower left quadrant
        subdivide(x+half,y+half,half)  # lower right quadrant
        subdivide(x+half,y,half)       # upper right quadrant
    }
    ELSE{
    	save the information about the square
    }
}

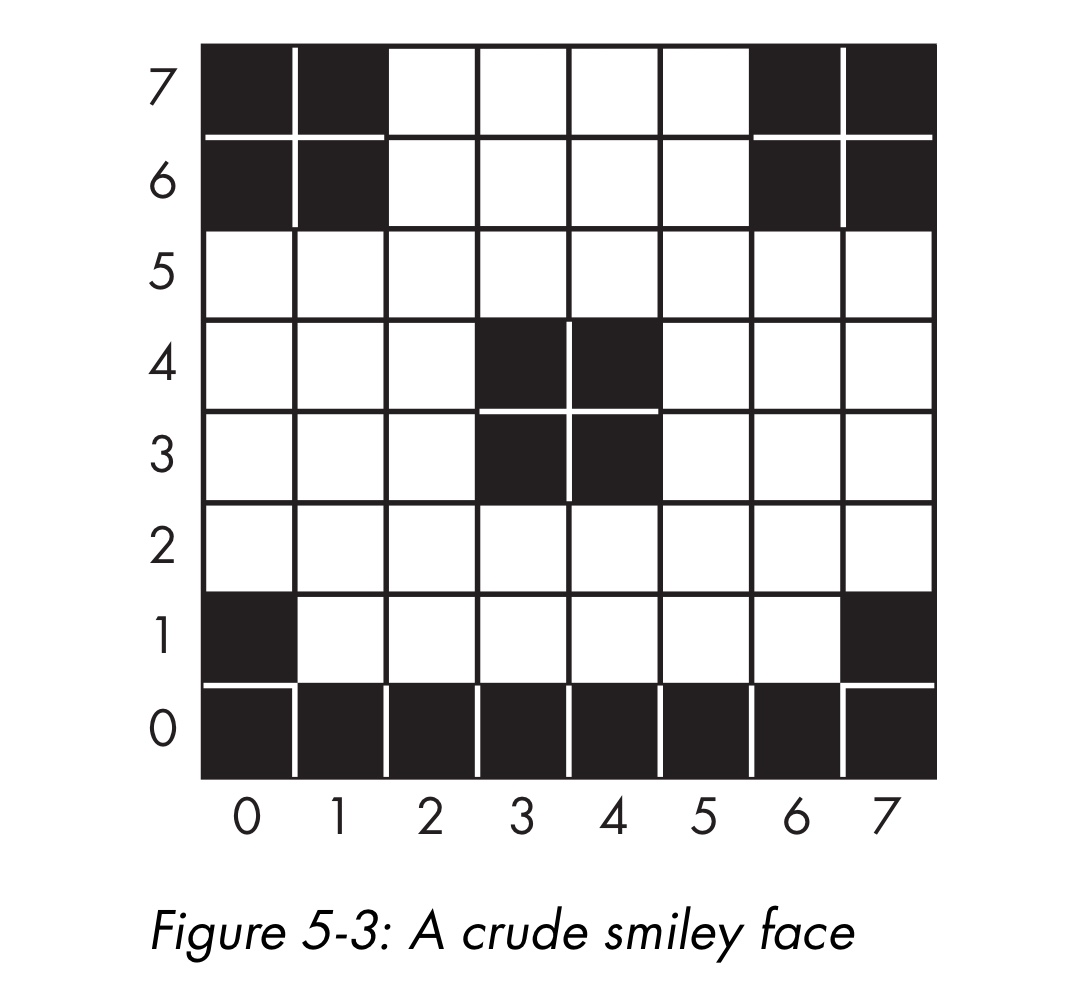
• subdivide function은 왼쪽 아래, 왼쪽 위, 오른쪽 위, 오른쪽 아래 순서로 이미지를 색이 똑같은 정사각형으로 나눔.
• 이를 tree 구조로 표현하면 아래와 같음

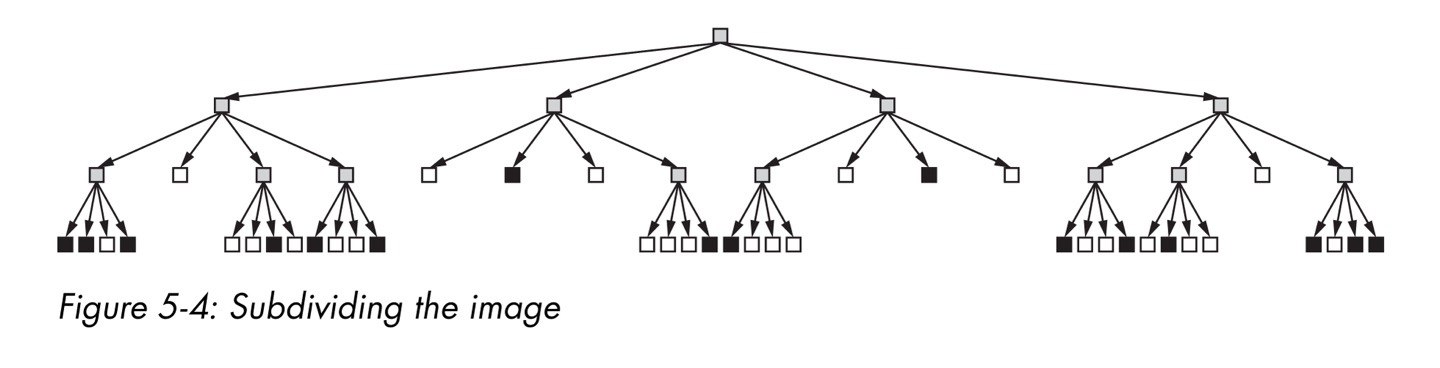
• 위의 그림에서 회색이 아닌 사각형은 40개로 원래 이미지 픽셀 수인 64개보다 줄어들었다는 것을 알 수 있음. 이는 저장해야 할 정보가 줄어들었다는 것.
• 위의 image subdivision은 Depth-First-Search로 동작하며 stack과 recursive call을 통해 구현할 수 있음.

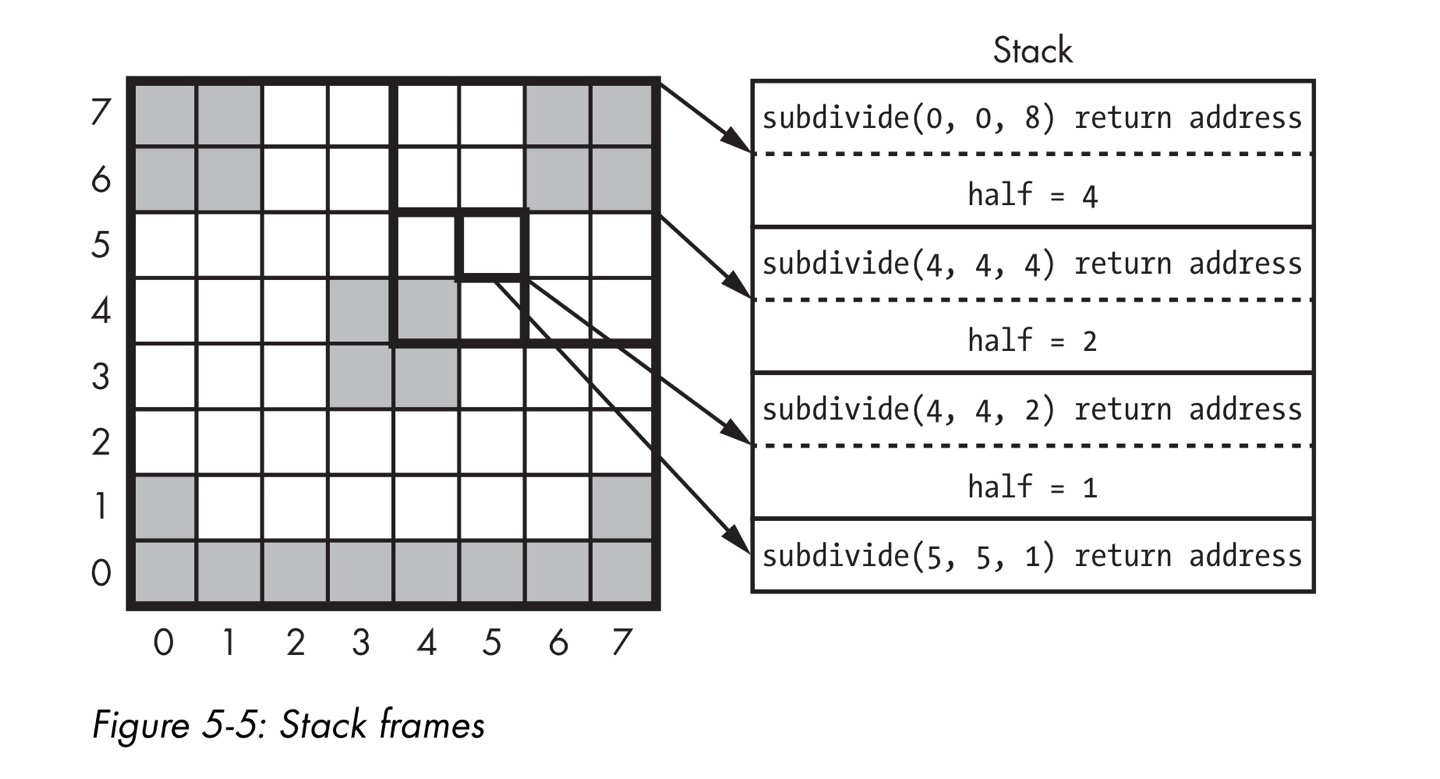
• Stack과 Stack Frame은 위와 같음.
• recursive call이 발생할 때마다 귀환할 주소와 해당 call의 parameter에 할당된 argument를 stack에 집어넣음.

Recursive Call : Fibonacci Sequence

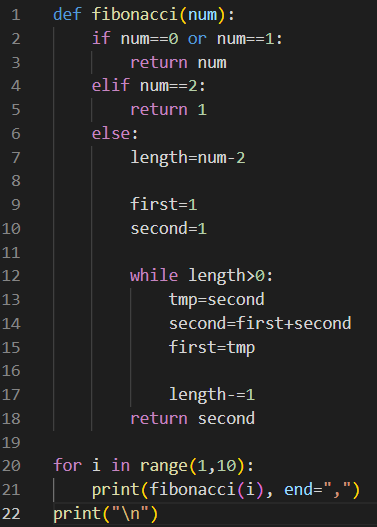
Python : using Recursive call

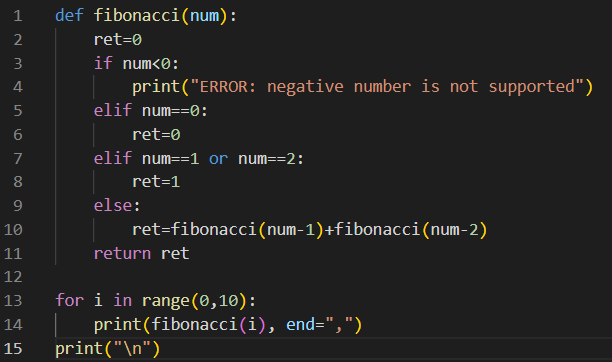
Python : using 'while'

Data Structures

Tree and Graph

• Graph
  • node와 node를 연결하는 edge로 구성된 data structure
  • object들의 network를 모델링하는데 사용
  • 통신 기기 간의 네트워크, 지하철 노선도 등이 대표적인 예
  • Artificial Neural Network등의 구현에 사용되는 computational graph 등이 유명.
• Tree
  • Directed Acyclic Graph에서 graph 내의 모든 node와 path가 존재하는 root node라는 것이 1개 있는 data structure
  • object들의 hierarchy를 모델링하는데 사용
  • Class들의 inherence diagram이 예
  • binary tree 등이 자주 나옴.
• Data Structure
  • Data를 표현하고 관리하고 처리하기 위한 구조
  • stack, queue, graph, tree 등이 기본적인 data structure로 linked list 등으로 구현됨.

	Tree	Graph
Root node	1개의 root	해당 개념 없음
Parent node	root를 제외하고 모든 node는 1개의 parent node를 가짐	해당 개념 없음
Cycle	Cycle 존재하지 않는 acyclic graph의 일종	Cycle 가능
Direction	반드시 direction을 가지며, 이는 parent-child 관계를 나타냄	Undirected도 가능

Search Algorithm

• search는 많은 양의 데이터 중 원하는 데이터를 찾는 과정임.
• Graph, tree 등의 data structure 안에서 search algorithm을 적용

BFS(Breadth-First Search)

그래프 탐색
하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것

• root node에서 시작해서 인접한 node를 먼저 탐색하는 방법
• 쉽게 말해서 깊게 탐색하기 전 넓게 탐색하는 것
• 두 노드 사이의 최단 경로 혹은 임의의 결로를 찾고 싶을 때 사용

---

• 재귀적으로 동작하지 않음.
• 그래프 탐색의 경우 어떤 node를 방문했었는지 여부를 반드시 검사해야함. 그렇지 않을 경우 무한루프에 빠질 수 있음.
• Queue 자료 구조 사용 => FIFO 원칙으로 탐색

---

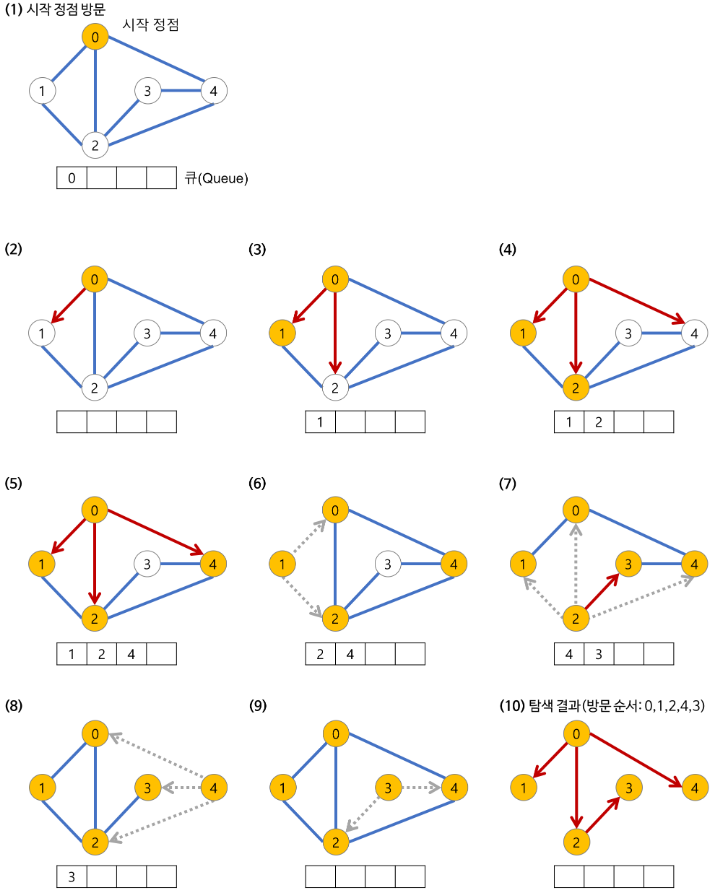
1. 시작 노드(a node) 방문

• queue에 방문된 node 삽입(enqueue)
• 초기 상태의 queue에는 시작 node만이 저장

2. Queue에서 꺼낸 node와 인접한 node들을 모두 차례로 방문

• queue에서 꺼낸 node 방문
• queue에서 꺼낸 node와 인접한 node들을 모두 방문. 인접한 node가 없다면 queue의 앞에서 node를 꺼냄(dequeue)
• queue에 방문된 node를 삽입(enqueue)

3. queue가 소진될 때까지 계속

DFS(Depth-First Search)

• root node에서 시작해서 다음 branch로 넘어가기 전에 해당 branch를 완벽하게 탐색하는 방법
• 넓게 탐색하기 전에 깊게 탐색하는 것
• 모든 node를 방문하고자 하는 경우에 사용
• DFS가 BFS보다 좀 더 간단하지만 단순 검색 속도 자체는 BFS에 비해 느림.

---

• 자기 자신을 호출하는 순환 알고리즘의 형태
• 전위 순회(Pre-Order Traversals)를 포함한 다른 형태의 tree 순회는 모두 DFS의 한 종류임.
• 그래프 탐색의 경우 어떤 node를 방문했었는지 여부를 반드시 검사해야함. 그렇지 않을 경우 무한루프에 빠질 위험이 있음.

---

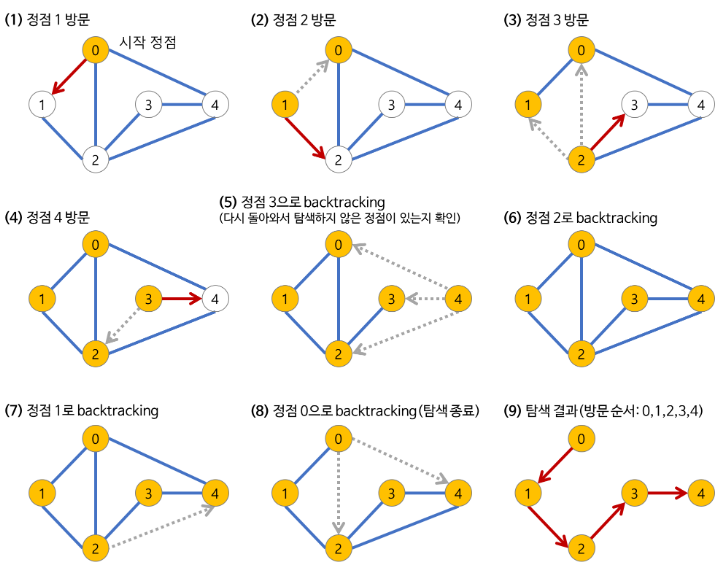
1. 시작 노드(a node) 방문
2. 시작 노드와 인접한 노드를 차례로 순회

• 시작 노드와 인접한 노드가 없다면 종료

3. a와 이웃한 node인 b node를 방문했다면 a와 인접한 또다른 node를 방문하기 전에 b의 이웃 node들을 전부 방문

• b를 시작 정점으로 DFS를 다시 시작하여 b의 이웃 node들을 방문

4. b의 분기를 전부 탐색했다면 다시 a에 인접한 정점들 중 아직 방문이 안 된 정점 찾기

• b의 분기를 전부 완변하게 탐색한 뒤에야 a의 다른 이웃 노드를 방문할 수 있다는 뜻
• 방문이 안 된 정점이 없으면 종료
• 있다면 다시 그 정점을 시작 정점으로 DFS 시작

References:
1) https://dsaint31.tistory.com/entry/CE-Subdivision-using-DFS
2) https://dsaint31.tistory.com/entry/Python-recursive-call-Fibonacci-Sequence
3) https://dsaint31.tistory.com/entry/CE-Tree-vs-Graph
4) Jonathan E., The Secret Life of Programs, pp. 122-124