
Graph?🤷🏻♂️
그래프란 노드(또는 vertex라고도 부른다.)와 그 노드를 연결하는 간선(edge)을 하나로 모아 놓은 비선형 자료 구조이다. 그래프는 방향성에 따라 무방향(undirected) 그래프와 단방향(directed) 그래프로 나뉘며 간선에 가중치를 할당하는 가중치(weighted) 그래프가 있다. 이번 포스팅은 무방향 그래프를 주로 다루며, 구현 또한 무뱡향 그래프를 구현했다.
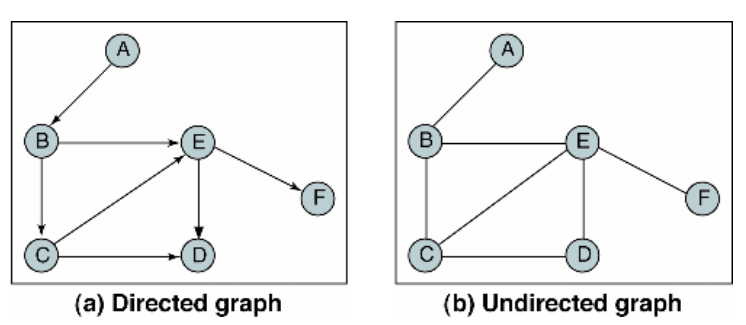
단방향 그래프는 간선에 방향성이 존재하는 그래프이며, A -> B로만 갈 수 있는 간선은 <A, B>로 표시한다. 무방향 그래프(undirected graph): 간선을 통해 양방향으로 이동하며, 정점A와 정점B를 연결하는 간선은 (A, B)와 같이 쌍으로 표현하는데, 단방향 그래프와는 달리 (A, B)와 (B, A)가 동일하다.
Graph 구현하기🛠
그래프의 표현방식은 인접 행렬(Adjacency matrix)과 인접 리스트(Adjacency list) 방식으로 나눌 수 있다.
인접 리스트(Adjacency list)
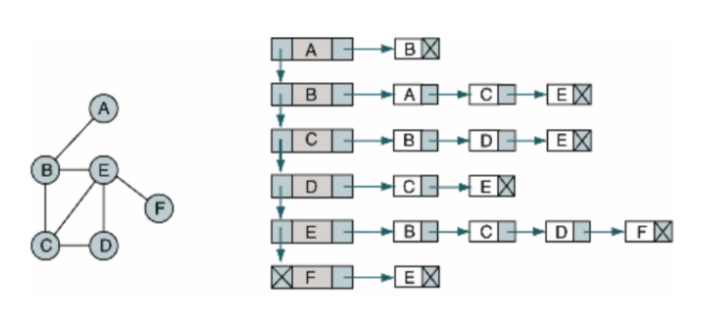
인접 리스트(Adjacency List)로 그래프를 표현하는 것이 가장 일반적인 방법이라고 하며, 그래프 내에 적은 숫자의 간선만을 가지는 경우에 용이하다고 한다. 각각의 정점에 인접한 정점들을 리스트로 표시한 것이다. 배열이나 연결리스트 등을 이용해서 구현이 가능하다. 특징은 연결된 간선의 정보만을 저장하여 O(E)의 공간을 요구하여 공간 효율성은 우수하지만 각 정점들의 연결 여부 확인을 위해 O(v)의 시간 복잡도를 가진다.
인접 행렬(Adjacency matrix)
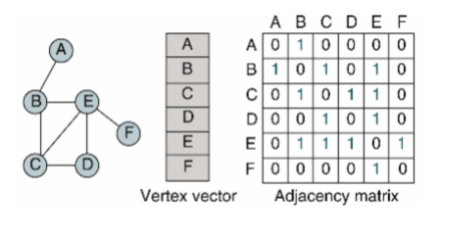
인접 행렬은 정점들을 2차원 배열로 구현한 것이다. 인접 행렬은 그래프에 간선이 많이 존재하는 밀집 그래프의 경우에 용이하며, 간선의 수와 무관하게 항상 n^2개의 메모리 공간이 필요하고, 특정 노드의 인접 노드들을 탐색하기위해선 모든 노드들을 확인해야하지만, 정점간의 연결여부 확인 시 O(1)의 시간을 요구한다.
구현
.png)
