너비 우선 탐색(Breath-First Search)

그래프에서 탐색을 한다는 것은 특정 노드(Node)를 찾아가는 기법입니다. 노드를 탐색하는 기법에는 크게 두 가지로 나누어 지는데 하나는 너비 우선 탐색(BFS) 기법과 또 다른 하나는 깊이 우선 탐색(DFS) 입니다. 먼저, 너비 우선 탐색 알고리즘을 알아 보도록 하겠습니다.

1. BFS와 DFS 란?

BFS와 DFS는 대표적인 그래프 탐색 알고리즘으로 너비 우선 탐색(Breath First Search)는 정점들과 같은 레벨에 있는 노드들(형제 노드들)을 먼저 탐색하는 방식이고 깊이 우선 탐색(Depth Frist Search)은 정점의 자식들을 먼저 탐색하는 방식입니다.

글만 봐서는 이해가 힘들테니 아래의 그림을 보면 좀 더 위해가 쉬울 것입니다.

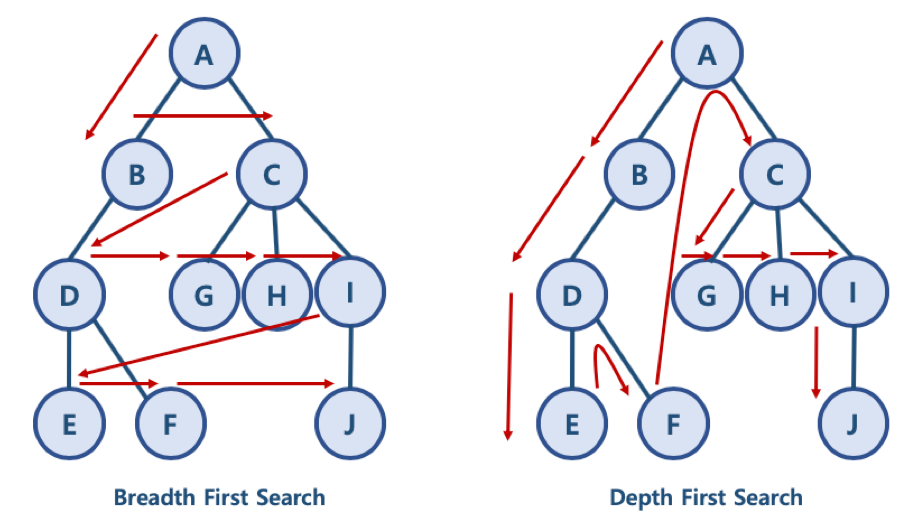
일단, 너비 우선 탐색이나 깊이 우선 탐색은 사이클(Cycle)이 없는 그래프에서 데이터를 탐색하는 방식입니다. 두 그래프는 동일하지만 화살표의 방향이 다르다는 것을 확인할 수 있습니다. 화살표는 탐색을 하기 위해서 노드를 이동하는 방향을 나타낸 것입니다.

그렇다면, BFS와 DFS의 방식이 어떻게 노드를 탐색하는지 비교해 보겠습니다.

• BFS 방식: A - B -C - D - G - H - I - E - F - J
  한 단계씩 내려가면서, 해당 노드와 같은 레벨에 있는 노드들(형제 노드들)을 먼저 순회

• DFS 방식: A- B - D - E - F - C - G - H - I - J
  한 노드의 자식을 타고 끝까지 순회한 후, 다시 돌아와 다른 형제들의 자식을 타고 내려가며 순회

즉, BFS 방식은 레벨마다 옆에 노드를 먼저 탐색을 하고 없으면 다음 레벨로 내려와서 탐색을 반복을 하고 DFS 방식은 노드를 타고 계속 내려와서 없으면 옆의 노드를 탐색하는 방식으로 설명할 수 있습니다. 따라서 BFS냐 DFS냐에 따라서 노드를 탐색하는 순서가 달라집니다.

2. 파이썬으로 그래프를 표현하는 방법

파이썬으로 BFS를 구현하는 방법을 알아보겠습니다. 먼저 BFS 알고리즘을 구현하려면 어떤 방식으로든 그래프를 만들어서 데이터를 저장해야 하는데 파이썬 같은 경우에는 파이썬에서 제공하는 딕셔너리와 리스트 자료 구조를 이용하면 그래프를 표현할 수 있습니다.

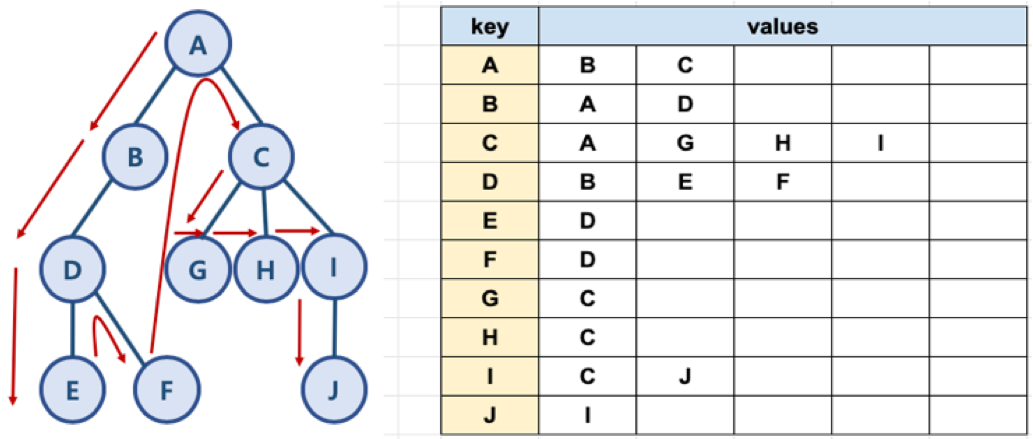
모든 노드들을 key로 만듭니다. 그리고 각 key에 대한 value는 해당 노드의 간선으로 연결된 인접 노드를 만듭니다. 예를 들면 'A'와 연결된 인접 노드는 'B', 'C'이고 이것을 파이썬으로 만든다면 [A] = ['B', 'C'] 로 만들 수 있습니다.

위의 표를 파이썬 딕셔너리로 다음과 같이 표현할 수 있습니다.

graph = dict()

graph['A'] = ['B', 'C']
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']

3. BFS 알고리즘 구현

이제 자료구조 큐(Queue)를 사용해서 BFS 알고리즘을 구현해 보도록 하겠습니다. BFS 알고리즘을 구현할 때는 방문이 필요한 노드들에 대한 정보를 가지고 있는 need_visit 큐와 방문한 노드를 순서대로 기입한 visited 큐를 생성하여 만들 것 입니다.

맨 처음에 need_visit 큐에는 key값인 'A'가 들어갑니다. 그리고 큐에서 'A'를 빼내어 visited 큐에서 'A'가 방문했는지를 체크합니다. 가장 처음이기 때문에 visited에는 'A'가 없으므로 'A'를 visited 큐로 넣어줍니다. 그리고 key값인 'A'의 value인 'B'와 'C'를 need_visit 큐에 순서대로 넣어주면 한 턴이 끝나게 됩니다.

visited = ['A']
need_visit = ['B', 'C']

두 번째 턴 부터는 위의 방법을 반복하게 됩니다. need_visit의 'B'를 need_visit에서 빼내어 줍니다.

B
visited = ['A']
need_visit = ['C']

'B'라는 데이터도 visited에 없으므로 visited에 넣어줍니다. 그리고 'B'의 value인 'A'와 'D'를 need_vist에 순서대로 넣어줍니다.

visited = ['A', 'B']
need_visit = ['C', 'A', 'D']

세 번째도 같은 방식으로 데이터를 넣어줍니다. 네 번째 턴에서도 위와 같은 방법을 반복을 하게 되는데

'A'
visited = ['A', 'B', 'C']
need_visit = ['D', 'A', 'G', 'H', I']

need_visit에서 빼낸 'A'는 visited에서도 있으므로 아무것도 안하고 끝나게 되고 다음으로 넘어가게 됩니다. 이런 방식으로 진행을 하게 되면 BFS를 설명할 때의 그림처럼 해당 노드들을 탐색하게 됩니다.

위의 방식을 이용하여 파이썬을 이용한 BFS 구현 코드입니다.

def bfs(graph, start_node):
    visited = list()
    need_visit = list()
    
    # need_visit에다가 맨 처음 노드를 넣어줌
    need_visit.append(start_node)
    
    # need_visit에 가져올 데이터가 없으면 종료
    while need_visit:
    	node = nees_visit.pop(0)
        
        # 해당 노드가 visited에 있는지 없는지 확인
        # 없으면 visited에 해당 노드를 넣고 value값을 need_visit에 넣어줌
        if node not in visited:
            visited.append(node)
            need_visit.extend(graph[node])
            
    return visit 

4. DFS 알고리즘 구현

앞서 BFS는 두 개의 큐를 이용하여 알고리즘을 구현할 수 있다고 설명했습니다. DFS는 need_visit 스택과 visited 큐, 두 개의 자료구조를 생성하여 DFS 알고리즘을 유사하게 구현할 수 있습니다.

BFS와 유사하게 맨 처음에 탐색을 할 노드를 need_visit에 넣고 시작을 합니다. 그리고 visited에 해당 노드가 있는지 확인을 하고, 노드가 없으면 visited에 노드를 넣고 그 해당 노드의 인접 정보를 need_visit 스택에 넣게 됩니다.

visited = ['A']
need_visit = ['B', 'C']

그 다음에는 BFS와 달리 DFS의 need_visit은 스택이기 때문에 맨 뒤에 있는 노드를 가져오게 됩니다.

C
visited = ['A']
need_visit = ['B']

그리고 visited에는 'C'가 없으므로 'C'를 넣어주고 'C'의 인접 노드들을 need_visit에 넣어줍니다.

visited = ['A', 'C']
need_visit = ['B', 'A', 'G', 'H', 'I']

이런식으로 확인을 하면 DFS 방식으로 탐색을 한다는 것을 확인할 수 있습니다.

DFS 방식을 이용한 파이썬 알고리즘 입니다.

def dfs(graph, start_node):
    visited, need_visit = list(), list()
    need_visit.append(start_node)
    
    while need_visit:
    	node = need_visit.pop()
        if node not in visited:
            visited.append(node)
            need_visit.extend(graph[node])
            
    return visited

5. 시간 복잡도

마지막으로 BFS와 DFS의 시간 복잡도를 계산을 해보면 노드 수(V), 간선의 수(E)로 한다면 while need_visit은 V + E 번 수행을 하게 됩니다.

따라서, 시간 복잡도는 O(V + E)가 됩니다.