최단 경로 알고리즘이란?

최단 경로 알고리즘은 두 노드를 잇는 가장 짧은 경로를 찾는 알고리즘입니다. 가중치 그래프(weighted)에서 간선(edge)의 가중치 합이 최소가 되도록 하는 경로를 찾는 것이 목적으로 코딩테스트에서 많이 나오지는 않지만 간혹 나오기 때문에 알아 두는 것이 좋다고 생각합니다.😱

코딩테스트에서 나오는 최단 경로 문제의 종류

1. 단일 출발 및 단일 도착(single-source and single destination shortest path problem) 최단 경로 문제

   • 그래프 내의 특정 노드 u에서 출발, 또 다른 특정 노드 v에 도착하는 가장 짧은 경로를 찾는 문제

2. 단일 출발(single-source and shortest path problem) 최단 경로 문제

   • 그래프 내의 특정 노드 u와 그래프 내 다른 모든 노드 각각의 가장 짧은 경로를 찾는 문제

3. 전체 쌍(all-pair) 최단 경로: 그래프 내의 모든 노드 쌍(u, v)에 대한 최단 경로를 찾는 문제

다익스트라 알고리즘은 하나의 정점에서 다른 모든 정점 간의 각각 가장 짧은 거리를 구하는 문제이므로 위의 최단 경로 문제 중 2번에 해당합니다.

다익스트라(Dijkstra) 알고리즘 로직

다익스트라(Dijkstra) 알고리즘은 첫 정점을 기준으로 연결되어 있는 정점들을 추가해 가며, 최단 거리를 갱신하는 기법으로 그래프 탐색의 대표적인 알고리즘인 너비 우선 탐색(BFS)과 유사합니다.

다익스트라 알고리즘의 다양한 변형 로직이 있지만, 가장 개선된 우선순위 큐를 사용하는 방식을 사용하겠습니다.

우선, 다익스트라 알고리즘을 설명을 하기 위한 그래프를 가져오겠습니다.

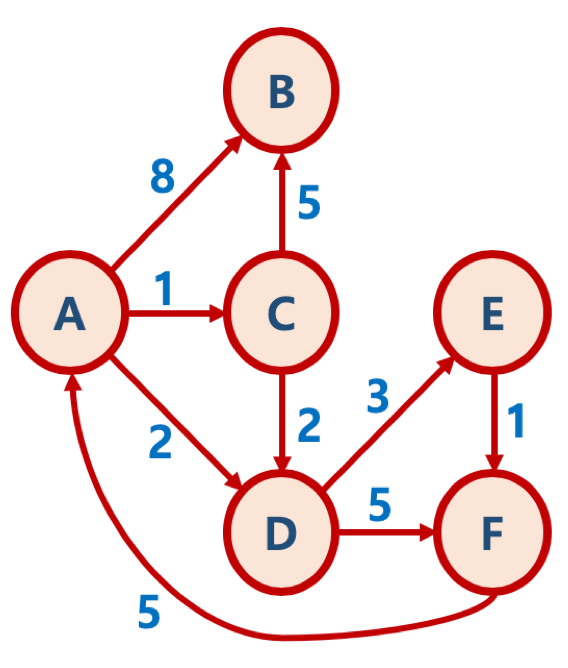
1단계: 초기화

첫 정점을 기준으로 배열을 선언하여 첫 정점에서 각 정점까지의 거리를 저장합니다.

• 초기에는 첫 정점의 거리를 0, 나머지는 무한대로 저장
• 우선순위 큐에 첫 정점(거리 0)만 넣음

2단계: 우선순위 큐에서 추출한 (A, 0) [노드, 첫 노드와의 거리]를 기반으로 인접한 노드와의 거리 계산

우선순위 큐에서 첫 정점과 인접한 노드를 거리를 비교하고 우선순위 큐에 넣습니다.

• 처음에는 첫 정점만 저장되어 있으므로, 첫 정점이 꺼내짐
• 첫 정점에 인접한 노드를 각각에 대해, 첫 정점에서 각 노드로 가는 거리와 현재 배열에 저장되어 있는 첫 정점에서 각 정점까지의 거리를 비교
• 배열에 저장되어 있는 거리보다, 첫 정점에서 해당 노드로 가는 거리가 더 짧을 경우, 배열에 해당 노드의 거리를 업데이트
• 배열에 해당 노드의 거리가 업데이트된 경우, 우선순위 큐에 넣음

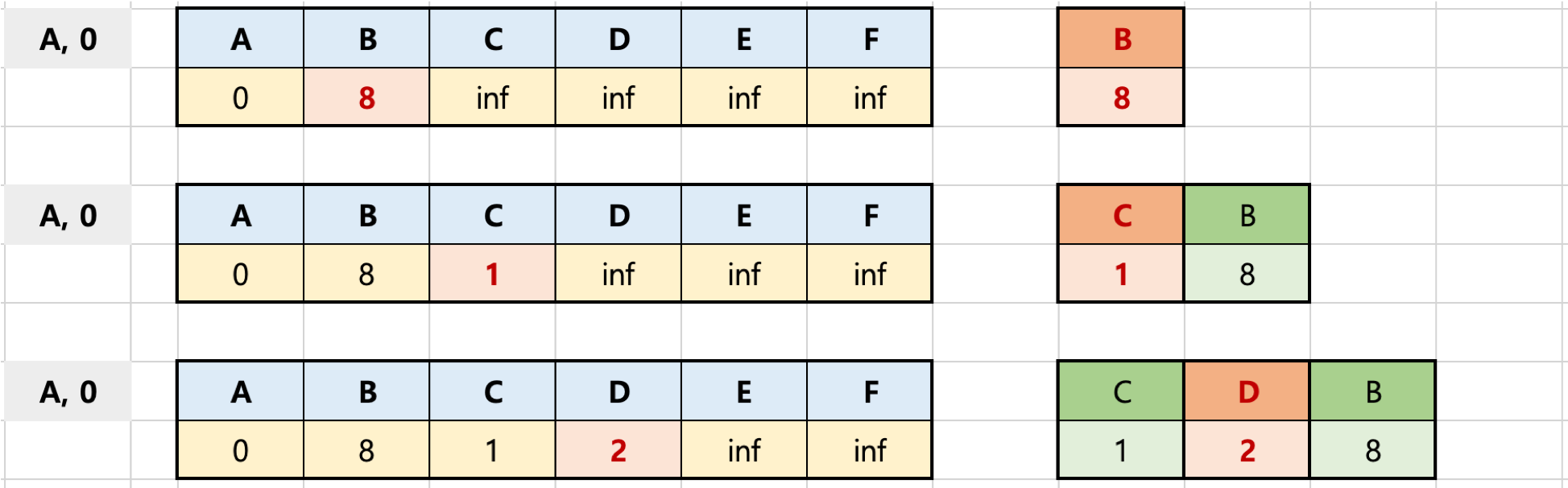
즉, 정점 이외에 모두 inf 였었으므로, 첫 정점에 인접한 노드들은 모두 우선순위 큐에 들어가고, 첫 정점과 인접한 노드간의 거리가 배열에 업데이트 됩니다. (노드를 순차적으로 방문하는 것이 너비 우선 탐색과 매우 유사합니다.)

3단계: 우선순위 큐에서 (C, 1)[노드, 첫 노드와의 거리]를 기반으로 인접한 노드와의 거리 계산

파이썬에서 우선순위 큐는 최소 힙(Min-Heap) 방식이기 때문 2단계 표에서 볼 수 있듯이 (C, 1), (D, 2), (B, 8)중 (C, 1)이 먼저 추출됩니다.

• 1단계까지의 A-B 최단 거리는 8인 상황
• A-C 까지의 거리는 (C, 1)에 인접한 B, D에서 C-B는 5, 즉 A-C-B는 1 + 5 =6 이므로, A-B 최단 거리 8보다 더 작은 거리를 발견
• 배열에 업데이트(배열에 업데이트 했으므로 A에서 B까지의 현재까지 발견한 최단 거리인 (B, 6) 값이 우선순위 큐에 넣어짐)
• C-D 의 거리는 2, 즉 A-C-D는 1 + 2 = 3 이므로, A-D의 현재 최단 거리인 2 보다 긴 거리, 따라서 D의 거리는 업데이트 되지 않음

4단계: 우선순위 큐에서 (D, 2)[노드, 첫 노드와의 거리]를 기반으로 인접한 노드와 거리 계산

지금까지 A의 인접 노드만 접근을 했다면, 이번에는 지금까지 접근하지 못했던 E와 F 거리가 계산됩니다.

• A-D 까지의 거리인 2에 D-E가 3 이므로 이를 더해서 (E, 5)
• A-D 까지의 거리인 2애 D-F가 5 이므로 이를 더해서 (F, 7)

5단계: 우선순위 큐에서 (E, 5)[노드, 첫 노드와의 거리]를 기반으로 인접한 노드와 거리 계산

A-E 거리가 5인 상태에서 E에 인접한 F를 가는 거리는 1, 즉 A-E-F는 5 + 1 = 6, 현재 배열 A-F 최단거리가 7로 기록되어 있으므로 (F, 6)으로 업데이트가 됩니다.

• 우선순위 큐에 (F, 6) 추가

6단계: 우선순위 큐에서 (B, 6), (F, 6) 를 순차적으로 추출해 각 노드 기반의 인접한 노드와의 거리 계산

예제 그래프에서는 B 노드는 다른 노드로 가는 루트가 없기 때문에 패스를 하고 F 노드는 A 노드로 가는 루트가 있으나, 현재 A-A가 0인 반면에 A-F-A는 6 + 5 = 11 이므로 업데이트가 되지 않습니다.

7단계: 우선순위 큐에서 (F, 7), (B, 8) 를 순차적으로 추출해 각 노드 기반의 인접한 노드와의 거리 계산

A-F 로 가는 하나의 루트의 거리가 7 이지만, 배열에서 이미 A-F 로 가는 현재 최단 거리가 6인 값이 있으므로 패스합니다. (B, 8)도 마찬가지로 A-B 거리가 6 이므로 계산할 필요가 없게 됩니다.

다익스트라 알고리즘 구현

import heapq

def dijsktra(graph, start):

    # 무한대로 넣음
    distances = {node: float('inf') for node in graph}

    # 그래프의 시작 정점 거리는 0으로 초기화
    distances[start] = 0

    # 모든 정점이 저장될 큐 생성
    queue = []

    # 그래프의 시작 정점과 거리를 최소힙에 넣음
    heapq.heappush.(queue, [distances[start], start])

    while queue:
        current_distance, current_node = heapq.heappop(queue)

        # 지금까지의 거리가 발견한 거리보다 더 작다면 다음 단계 패스
        if distances[current_node] < current_distance:
            continue

        # 인접노드, 거리 값
        for adjacent, weight in graph[current_node].items():
            distance = current_distance + weight

            # 최단거리를 발견했을 경우 거리를 업데이트
            if distance < distances[adjacent]:
                distances[adjacent] = distance
                heapq.heappush(queue, [distance, adjacent])

    return distance