액터 모델과 동시성 제어 - 사이클 탐색

소개

이전 포스팅에서 우리는 기초적인 동시성과 액터 모델에 대해 알아보았습니다. 하지만, 작성한 액터 모델에는 오버플로우를 발생시킬 가능성이 있었습니다. 바로 2개 이상의 액터가 서로를 구독하면 무한히 메시지가 돌면서 값이 계속 업데이트 되는 것이였죠. 이번 포스팅에서는 그래프 탐색 알고리즘을 이용해 문제가 되는 부분을 미리 찾아내는 작업을 해보겠습니다.

그래프

액터를 노드로 구독 관계를 간선으로 표현하면 $G = (V, E)$ 꼴의 그래프로 표현할 수 있습니다. 구독 관계는 방향성이 있기 때문에 유향 그래프(directed graph)로 볼 수 있습니다. 유향 그래프에서 사이클이 있는지 검사하는 것은 주어진 그래프가 유향 비순환 그래프(DAG, Directed Acyclic Graph)인지 판별하는 것입니다.

어떤 노드 $v$에서 출발해 간선을 따라 다시 노드 $v$로 돌아온다면 순환한다고 합니다. 이때 그래프에 순환하는 구조가 없다면(즉, 사이클이 없다면) 유향 비순환 그래프, 즉 DAG(directed acyclic graph)라고 합니다.

이 DAG를 검사하는 알고리즘은 여러가지가 있지만, 여기서는 DFS(깊이 우선 탐색)와 BFS(너비 우선 탐색) 방식을 사용할 것입니다.

깊이 우선 탐색(DFS)

깊이 우선 탐색은 이름 처럼 깊이(depth)를 우선으로 하는 탐색 알고리즘입니다. 즉, 그래프의 어떤 노드에서 출발해 한 경로를 따라 가능한 깊은 곳 까지 내려면서 그래프를 탐색합니다. 탐색 중 더 이상 방문할 노드가 없다면 왔던 길을 되돌아가는(backtrace) 방식을 사용합니다.

1. 시작 노드를 스택에 추가
2. 현재 스택의 맨 위에 있는 노드를 확인
	|방문하지 않은 인접 노드가 있으면 그 노드를 스택에 넣고 방문 처리 
	| 방문하지 않은 인접 노드가 없다면 스택에서 해당 노드를 꺼냄
3. 2번 과정을 스택이 빌 때까지 반복

너비 우선 탐색(BFS)

너비 우선 탐색은 너비(breadth)를 우선으로 하는 탐색 알고리즘입니다. DFS가 한 노드에서 출발해 가장 깊은 곳 까지 내려가는 방식을 사용했다면, BFS는 특정 노드에서 시작해 인접한 노드들을 모두 탐색하고, 방문했던 노드에서 인접한 노드들을 또 탐색하는 방식으로 동작합니다.

1. 시작 노드를 큐에 넣고 방문 처리
2. 큐에서 노드를 꺼내고 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 넣고 방문 처리
3. 2번 과정을 큐가 빌 때까지 반복

위상정렬

위상 정렬을 방향성이 있는 그래프 구조에서 사용하는 알고리즘으로, 그래프의 노드들 선형으로 정렬하는 역할을 합니다. 이때 나열되는 순서는 간선들의 방향을 따라야 합니다. 예를 들어, 노드 A에서 노드 B로 향하는 간선이 있다면 A는 B 보다 앞서야 합니다. 이렇게 위상 정렬은 노드들의 선후관계를 유지하며 모든 노드를 나열할 수 있게 해줍니다.

1. BFS를 사용, 그래프의 모든 노드를 방문
2. 각 노드에 대해 BFS를 수행 
	| 더 이상 방문할 수 있는 인접 노드가 없다면, 해당 노드를 리스트의 앞쪽에 추가
3. 완료

참고로 위 세 알고리즘 모두 시간 복잡도는 $O(V+E)$를 가집니다. $V$는 그래프 내의 노드의 수를, $E$는 간선의 수를 의미합니다. 또한 공간 복잡도는 $O(V)$입니다.

구현

이제 각 알고리즘을 구현하면서 어느 알고리즘이 더 효율적인지 벤치마크를 돌려보면서 비교해보겠습니다. 벤치마크는 러스트의 criterion을 사용했습니다.

DFS, BFS 그리고 위상 정렬 순으로 본 뒤, 벤치마크 순서대로 보겠습니다. 먼저 DFS의 구현입니다.

impl ActorPool {
	pub fn detect_cycle_dfs(&self, actor_id: usize) -> Result<bool, ActorError> {
        let actor = self.get_actor_info(actor_id)?;

        let mut visited = HashSet::new();
        let mut stack = Vec::new();

        visited.insert(actor_id);
        stack.push(actor);

        while let Some(curr_actor) = stack.pop() {
            let subs = curr_actor.get_subscribers();

            for sub in subs {
                if visited.contains(&sub) {
                    return Ok(true);
                }

                let sub_actor = self.get_actor_info(sub)?;
                stack.push(sub_actor);
                visited.insert(sub);
            }
        }

        Ok(false)
    }
}

이 코드에서 시작 노드는 actor입니다. 이 노드에서 출발해 방문한 모든 노드는 visited에 저장됩니다. 탐색 중에 노드의 하위 노드(구독자)가 이미 visited에 있다면, 그래프에 사이클이 존재한다는 것이므로true를 반환해 사이클을 판별할 수 있습니다.

BFS의 구현도 보겠습니다.

impl ActorPool {
	pub fn detect_cycle_bfs(&self, actor_id: usize) -> Result<bool, ActorError> {
        let actor = self.get_actor_info(actor_id)?;

        let mut visited = HashSet::new();
        let mut q = VecDeque::new();

        visited.insert(actor_id);
        q.push_back(actor);

        while let Some(curr_actor) = q.pop_front() {
            let subs = curr_actor.get_subscribers();

            for sub in subs {
                if visited.contains(&sub) {
                    return Ok(true);
                }

                let sub_actor = self.get_actor_info(sub)?;
                q.push_back(sub_actor);
                visited.insert(sub);
            }
        }

        Ok(false)
    }
}

DFS와 비슷하지만, 스택 대신 큐를 사용하는데 collections::VecDeque를 사용했습니다. VecDeque는 양쪽 끝에서의 삽입과 삭제가 효율적으로 이루어지는 동적 배열로 구성된 큐입니다. 사이클을 판별하는 방법은 DFS와 같습니다.

마지막으로 위상정렬의 구현을 보겠습니다. 이때 그래프 탐색에는 BFS 방식을 사용했습니다.

impl ActorPool {
	pub fn detect_cycle_topological_sort(&self, actor_id: usize) -> Result<bool, ActorError> {
        // map to store the in-degree of each actor
        let mut in_degree: HashMap<usize, i32> = HashMap::new();

        let init_actor = self.get_actor_info(actor_id)?;
        let init_subs = init_actor.get_subscribers();

        in_degree.insert(actor_id, 0);

        for sub in init_subs {
            in_degree.insert(sub, 0);
        }

        // calculate the in-degree of each node in the subset
        for (_, actor) in self.actor_list.lock().unwrap().iter() {
            let subs = actor.get_subscribers();

            for sub in subs {
                if let Some(degree) = in_degree.get_mut(&sub) {
                    *degree += 1;
                }

                in_degree.insert(sub, 1);
            }
        }

        // queue to store nodes with in-degree of 0
        let mut q: VecDeque<usize> = VecDeque::new();

        // add nodes with in-degree of 0 to the queue
        for (id, degree) in in_degree.iter() {
            if *degree == 0 {
                q.push_back(*id);
            }
        }

        while let Some(curr_id) = q.pop_front() {
            // get current actor and its subscribers
            let curr_actor = self.get_actor_info(curr_id)?;
            let curr_subs = curr_actor.get_subscribers();

            for sub in curr_subs {
                if let Some(degree) = in_degree.get_mut(&sub) {
                    *degree -= 1;

                    // if in-degree becomes 0, add the subscriber to the queue
                    if *degree == 0 {
                        q.push_back(sub);
                    }
                }
            }
        }

        Ok(in_degree.values().any(|&degree| degree != 0))
    }
}

위상정렬을 이용해서 사이클을 판별하는 방법의 기본 전제는 “사이클이 없는 그래프에서만 정렬이 가능”하다 입니다. 따라서 위상 정렬을 적용할 수 없는 노드가 있다면 사이클이 있다고 판별할 수 있습니다. 이 함수의 구조는 다음과 같습니다.

1. 방문 차수(In-degree, 이하 차수) 계산: 방문 차수는 다른 노드에서 들어오는 간선의 수를 의미하며, 이 차수를 계산합니다. 그래프에 사이클이 없다면, 반드시 하나 이상의 노드는 방문 차수가 0이 되어야 합니다.
2. 큐 초기화: 계산된 차수를 바탕으로, 큐에 차수가 0인 노드를 추가합니다.
3. 정렬 적용: 큐에서 노드를 하나씩 꺼낸 뒤, 그 노드가 가리키는 노드(subscriber)의 차수를 1씩 감소시킵니다. 이후 차수가 0이 된 노드를 큐에 추가합니다. 이 과정을 큐가 빌 때까지 반복합니다.
4. 사이클 유무 판단: 모든 노드를 처리한 후에도 in-degree가 0이 아닌 노드가 있다면 그래프에는 사이클이 존재한다는 의미입니다. 따라서 마지막에 in-degree가 있는지 확인하고, 만약 있다면 true를 반환합니다.

위 세 알고리즘은 특정 액터에 하위 액터(구독자)를 추가할 때 사이클이 생기는지 검사하는 목적이라 전체 액터 그래프를 검사하지 않습니다. 만약 그래프 전체에서 사이클을 판별할 때는 특정 액터의 ID를 받는 대신 그래프를 받는 식으로 수정해야 합니다.

아무튼, 이렇게 세 가지 알고리즘을 구현해 봤습니다. 이제 벤치마크를 돌려보면서 어느 알고리즘이 효율적인지, 그리고 그게 왜 다른 알고리즘 보다 효율적인지 알아보겠습니다.

---

벤치마크

벤치마크는 criterion을 이용했습니다.

// rustor/benches/benchmark.rs

use criterion::{criterion_group, criterion_main, Criterion, BenchmarkId, black_box};
use rustor::model::actor::ActorPool;

fn create_large_graph(n: usize) -> ActorPool {
    let total_actors = n;

    let pool = ActorPool::new();
    let mut actor_ids: Vec<usize> = Vec::new();

    for _ in 0..total_actors {
        let actor_id = pool.create_actor();
        actor_ids.push(actor_id);
    }

    for i in 1..total_actors {
        pool.subscribe(actor_ids[i], vec![actor_ids[i - 1]])
            .unwrap();
    }

    // create cycle by making the last actor subscribe to the first actor
    pool.subscribe(actor_ids[0], vec![actor_ids[total_actors - 1]])
        .unwrap();

    pool
}

fn benchmark(c: &mut Criterion) {
    let pool = create_large_graph(1500);

    c.bench_function("dfs_cycle_detection", |f| {
        f.iter(|| pool.detect_cycle_dfs(0).unwrap())
    });

    c.bench_function("bfs_cycle_detection", |f| {
        f.iter(|| pool.detect_cycle_bfs(0).unwrap())
    });

    c.bench_function("topological_sort_cycle_detection", |f| {
        f.iter(|| pool.detect_cycle_topological_sort(0).unwrap())
    });
}

criterion_group!(benches, benchmark);
criterion_main!(benches);

create_large_graph는 거대한 원형구조의 액터 그래프를 생성합니다. 이제 cargo bench 명령으로 벤치마크를 실행하면 됩니다.

벤치마크의 결과는 결론부터 말하자면, 위상정렬이 압도적으로 빨랐고 그 다음으로 BFS, DFS 순이였습니다. 그럼 이제 왜 이런 결과가 나왔는지 각 알고리즘의 특성을 비교해보면서 분석해보겠습니다. 결과 그래프는 모두 Mean 그래프를 이용했습니다.

DFS vs. BFS

위상정렬의 결과를 보기 전에, 먼저 DFS와 BFS의 결과를 비교해보고 왜 이런 속도 차이가 나타났는지 비교해보겠습니다.

	DFS	BFS
그래프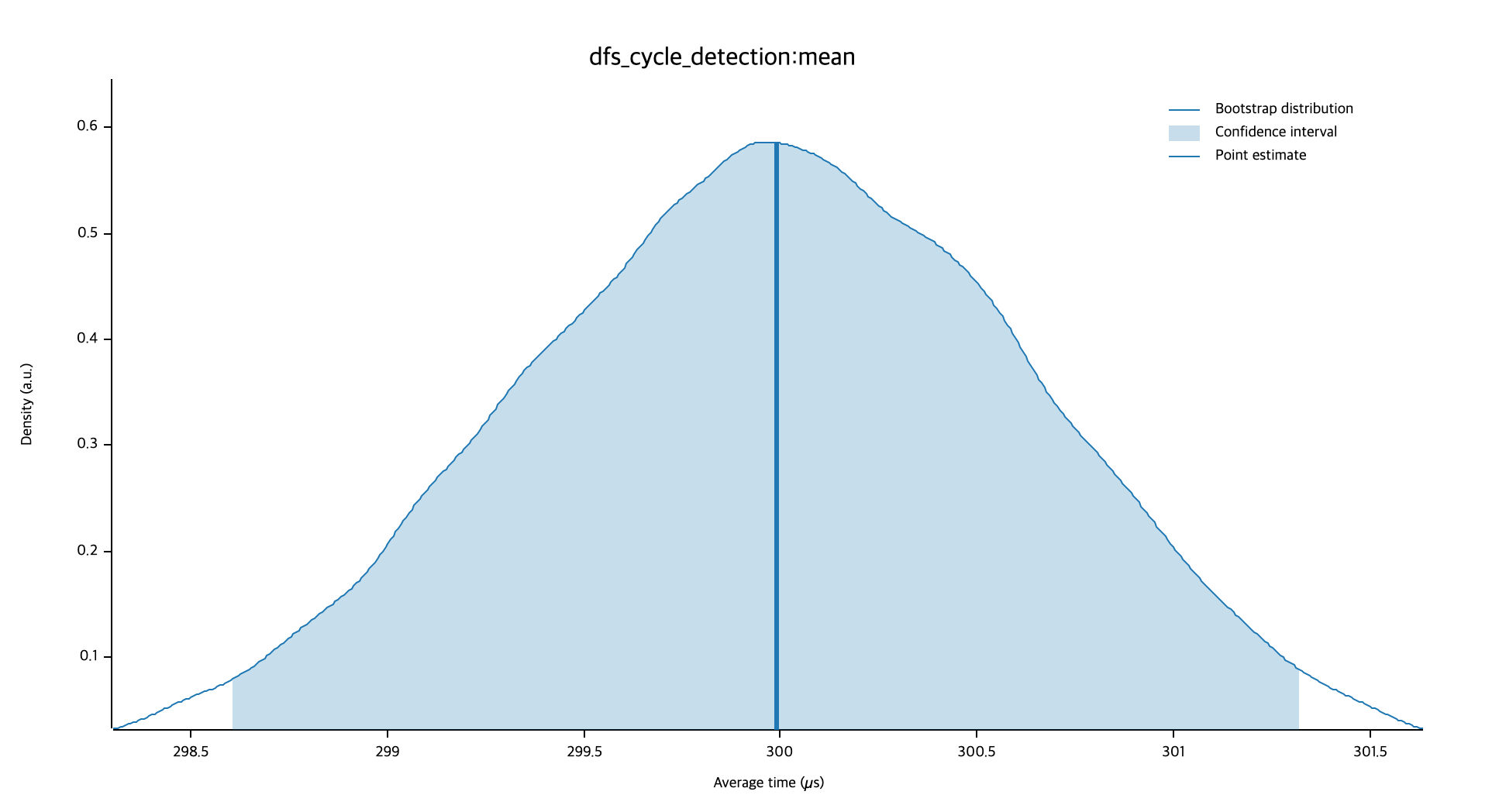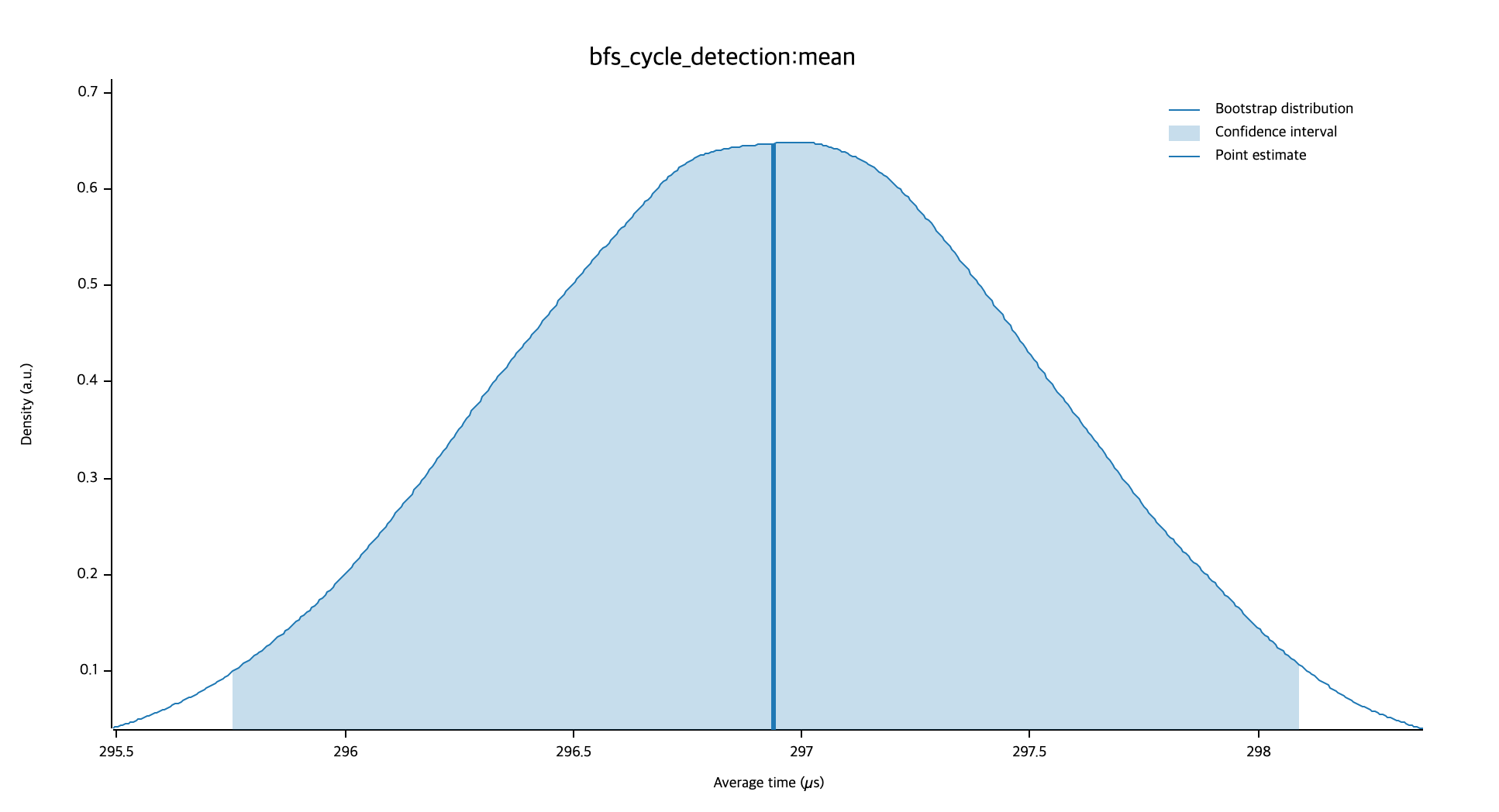
평균 시간	~300 µs	~296 µs

DFS, BFS 모두 시간 복잡도와 공간 복잡도는 $O(V+E)$, $O(V)$를 가지지만, 그래프를 보면 BFS가 DFS 보다 근소한 차이로 빨랐습니다. 이 차이는 두 알고리즘의 특성에서 기인합니다. DFS는 특정 노드의 자식 노드들을 모두 방문한 다음에 다른 노드로 넘어가기 때문에, DFS는 사이클을 방문하더라도 그 사이클의 모든 노드를 방문해야합니다. 반면에, BFS는 특정 노드와 같은 레벨의 노드를 우선적으로 탐색하기 때문에 특정 레벨에서 사이클을 탐지하면 탐색을 중료할 수 있습니다.

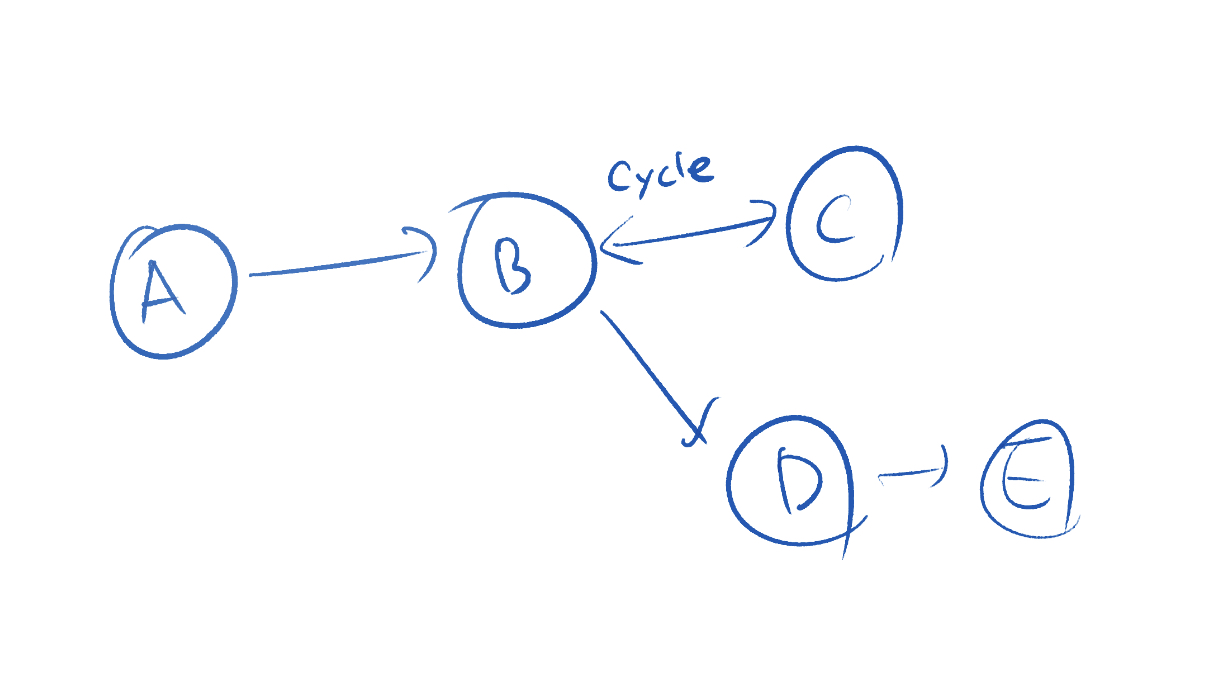
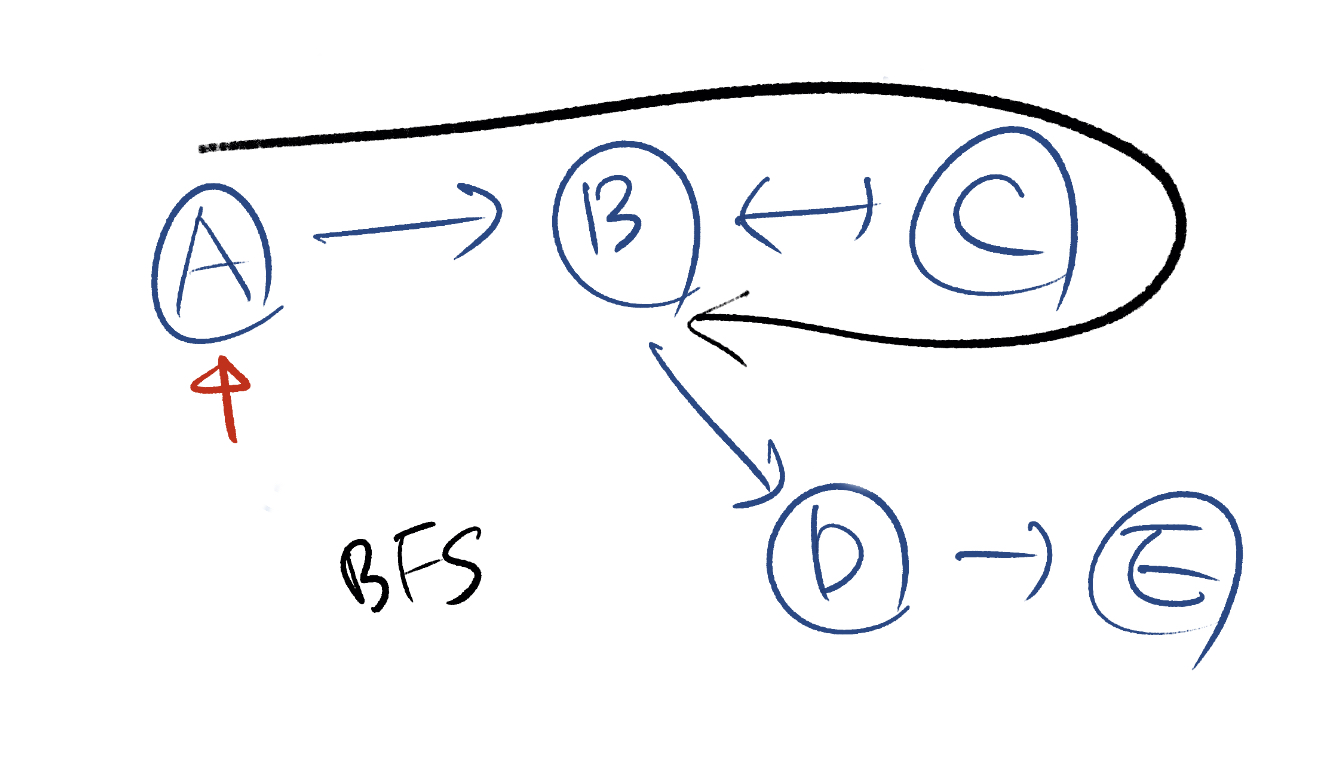
예를 들어 아래와 같은 그래프가 있다고 가정해보겠습니다. 화살표는 노드의 구독 관계를 나타냅니다.

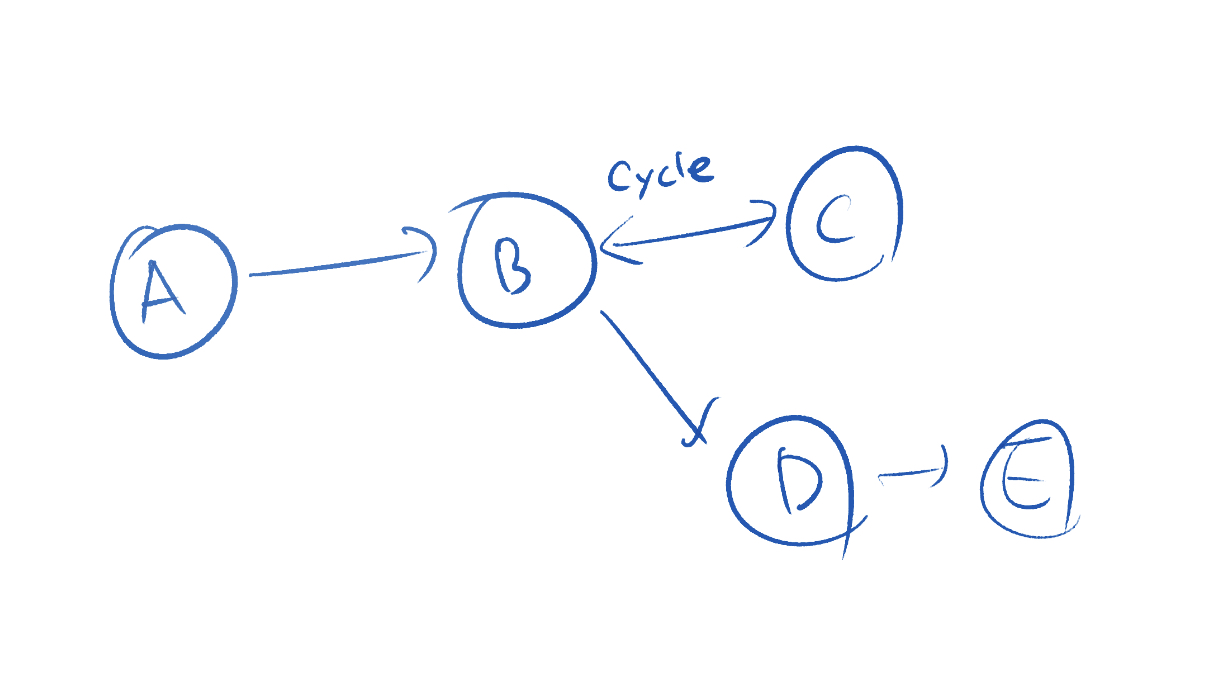
그림에서 보이듯, 사이클은 노드 B와 노드 C 사이에 있습니다. 만약 사이클이 없는 경우 DFS, BFS 모두 A, B, C, D, E 노드를 방문합니다.

하지만, 사이클이 있는 경우 BFS와 DFS는 방문하는 노드의 수에서 차이가 나타납니다. DFS 방식은 탐색 중 사이클을 찾아도 그 사이클의 하위 노드를 전부 방문해야 하지만, BFS의 경우 사이클을 발견하자마자 탐색을 종료합니다. 즉, 위 그래프에서 BFS가 방문하는 노드는 A, B, C 세개이기 때문에 성능상 차이가 발생합니다.

위 벤치마크에서는 단순히 거대한 원형 구조의 그래프를 탐색하기 때문에 약간의 차이가 나는 걸로 결과가 나왔지만, 좀 더 복잡한 관계의 그래프에서는 확연한 차이가 나타날 것으로 예상합니다.

BFS vs. 위상 정렬

이제 BFS와 위상정렬을 비교해보겠습니다. 위상정렬의 벤치마크 결과는 다음과 같습니다. BFS의 평균 실행 시간인 295.75 µs에 비교하면 위상정렬의 144.42 µs는 2배 이상 빠릅니다. 위상정렬을 구현할 때 BFS 방식을 이용해 노드를 탐색했는데 왜 이런 결과가 나왔을까요?

	BFS	위상 정렬
그래프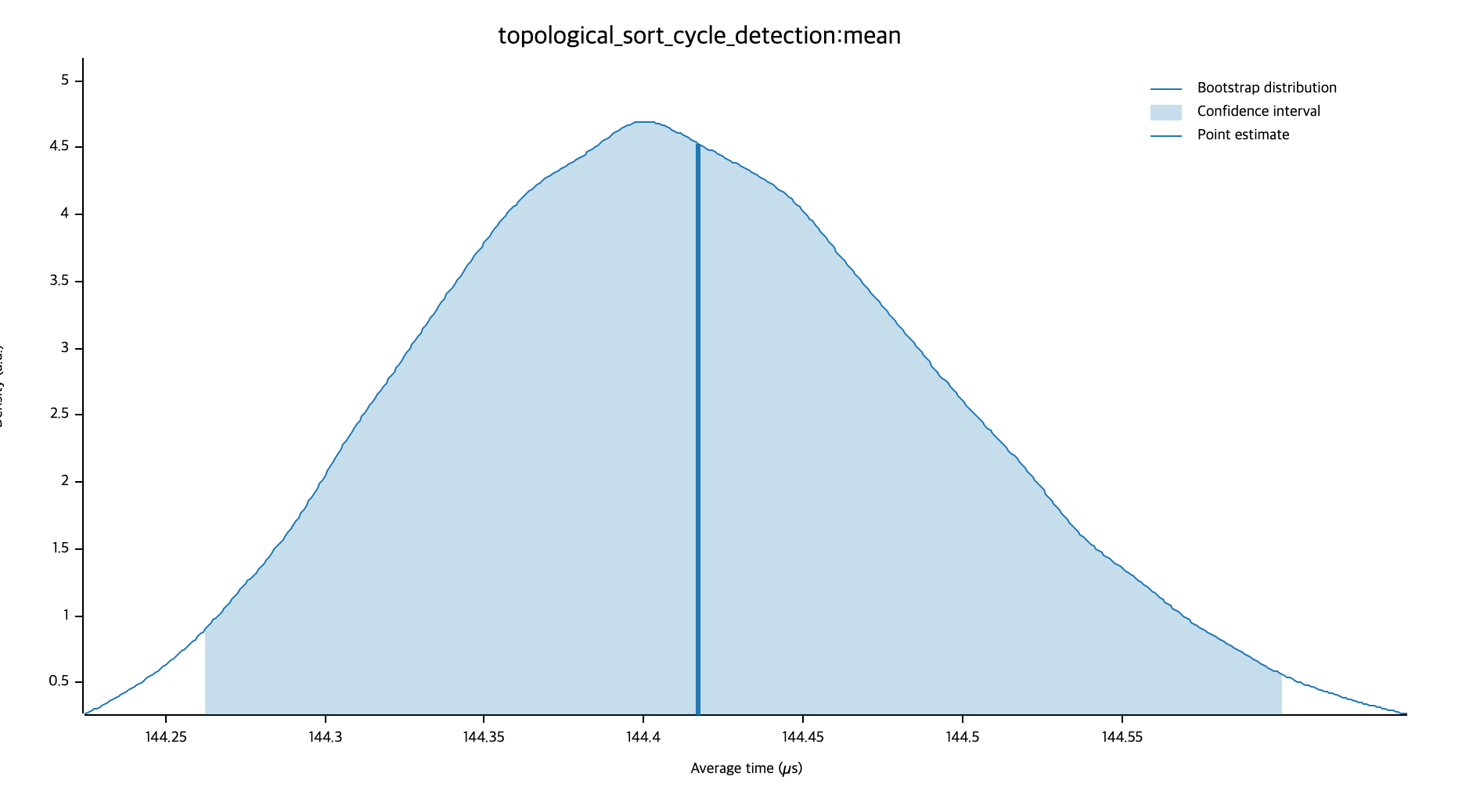
평균 시간	~296 µs	~144 µs

위상정렬과 BFS 모두 시간 복잡도는 $O(V+E)$를 가지고, 공간 복잡도 역시 둘 다 큐를 사용하기 때문에 $O(V)$의 복잡도를 가집니다. 하지만, 위상정렬은 BFS와 달리 차수를 계산하면서 노드를 방문하기 때문에 그래프의 구조를 좀 더 효과적으로 분석할 수 있고, 이로인해 실행 시간의 차이가 발생합니다.

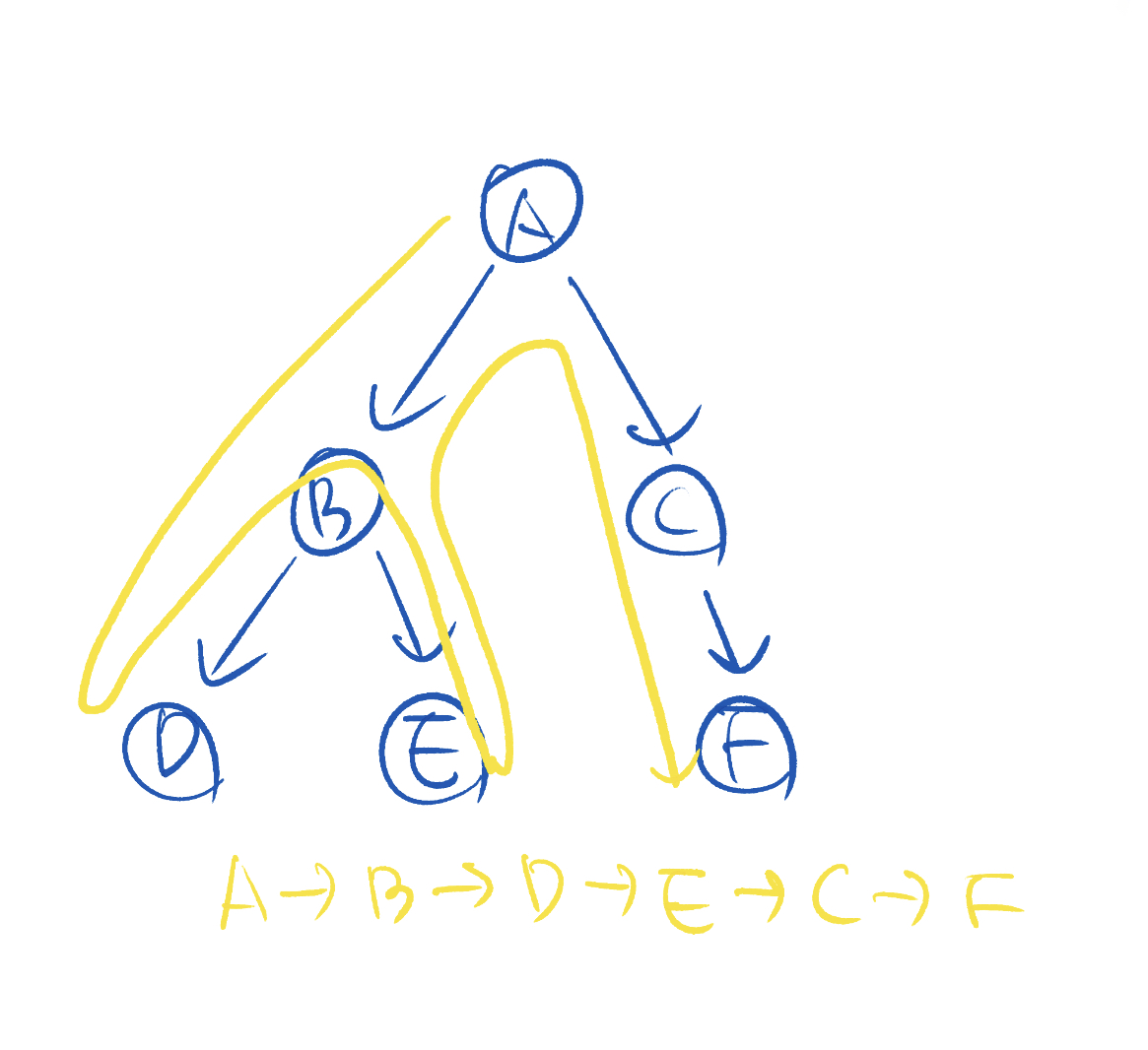
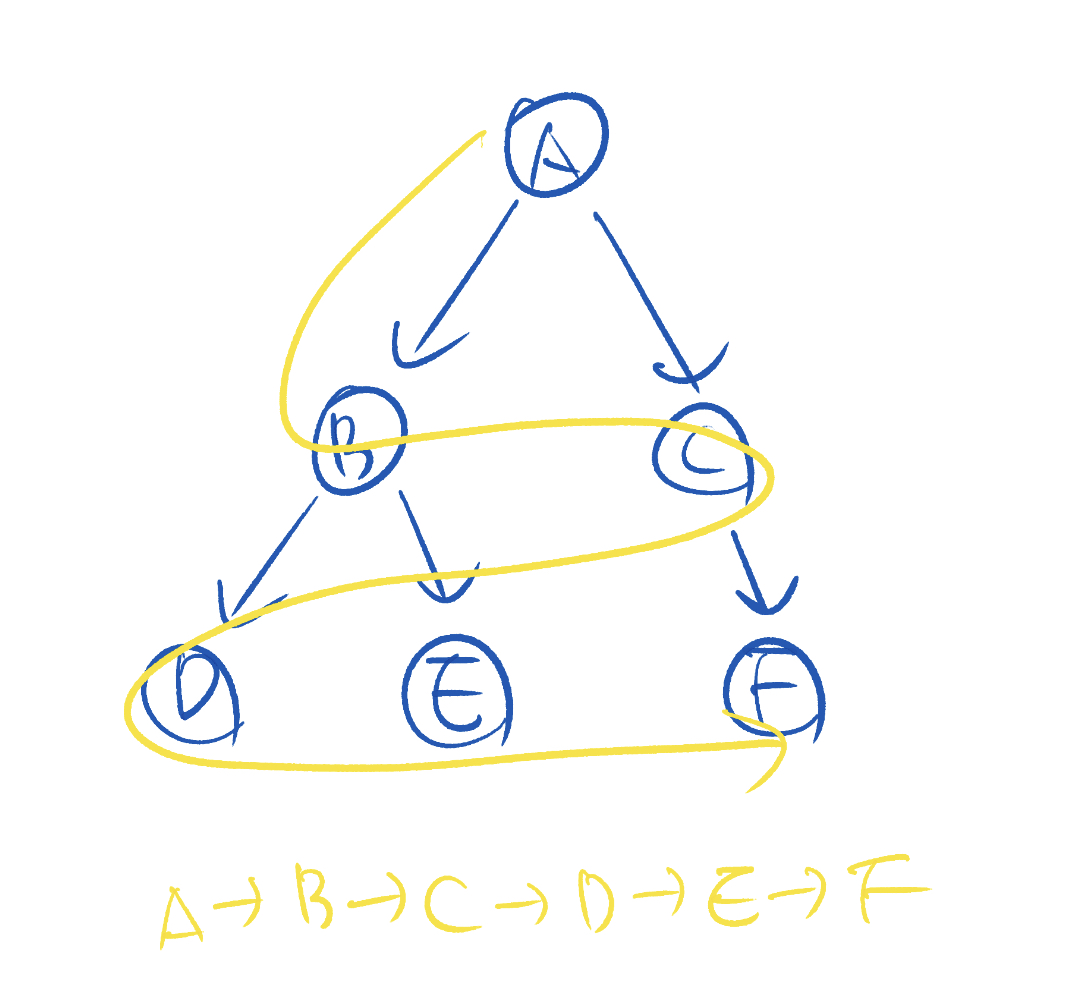
그렇다면 왜 차수가 이런 차이를 만들어냈을까요? 왜냐하면 진입 차수는 특정 노드의 의존성(dependency)를 파악하는데 도움이 되기 때문입니다. 다시 위에 있는 그래프 그림을 볼까요? 각 노드의 진입 차수는 A는 0, 나머지 B, C, D, E는 전부 1입니다. 이 그래프에서 위상 정렬이 진행되는 과정과 사이클을 찾는 과정은 아래와 같습니다.

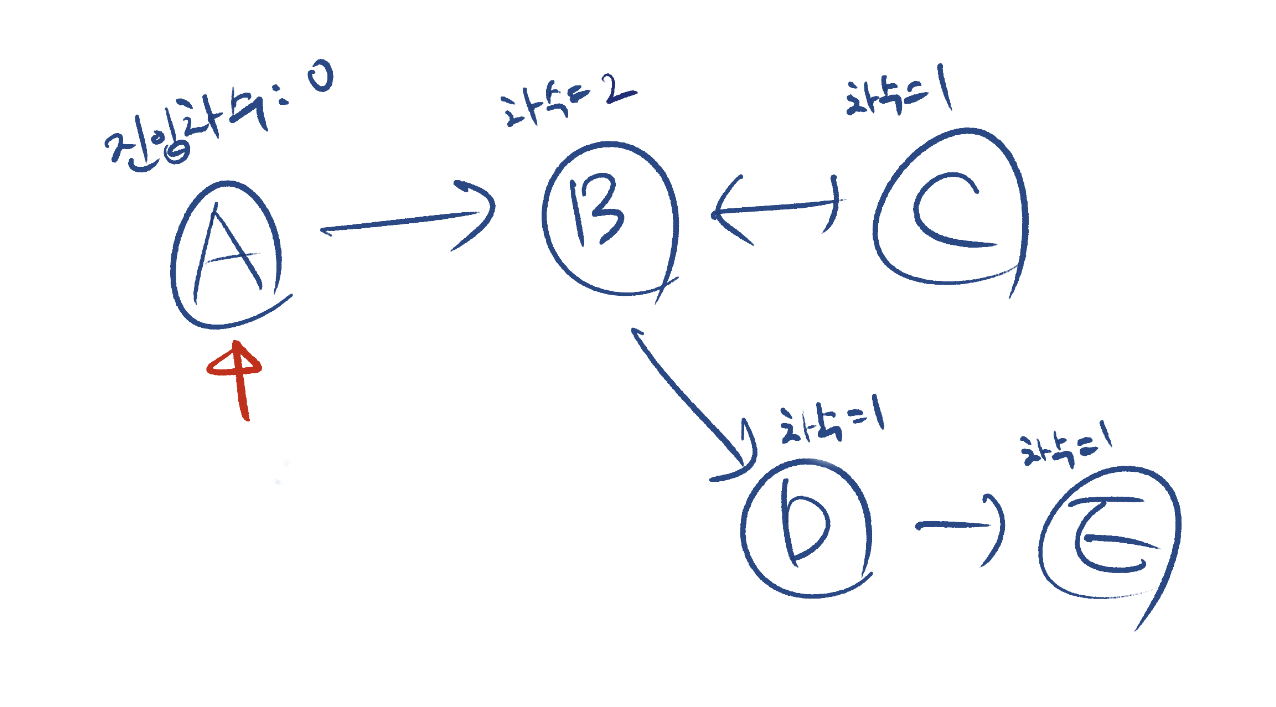
먼저 진입 차수가 0인 노드를 찾습니다. 이 경우 노드 A입니다. 따라서 노드 A를 먼저 방문하고 이 노드를 지나는 간선을 전부 제거합니다. 그럼 그래프는 아래와 같이 변합니다. (편의상 노드 A는 생략)

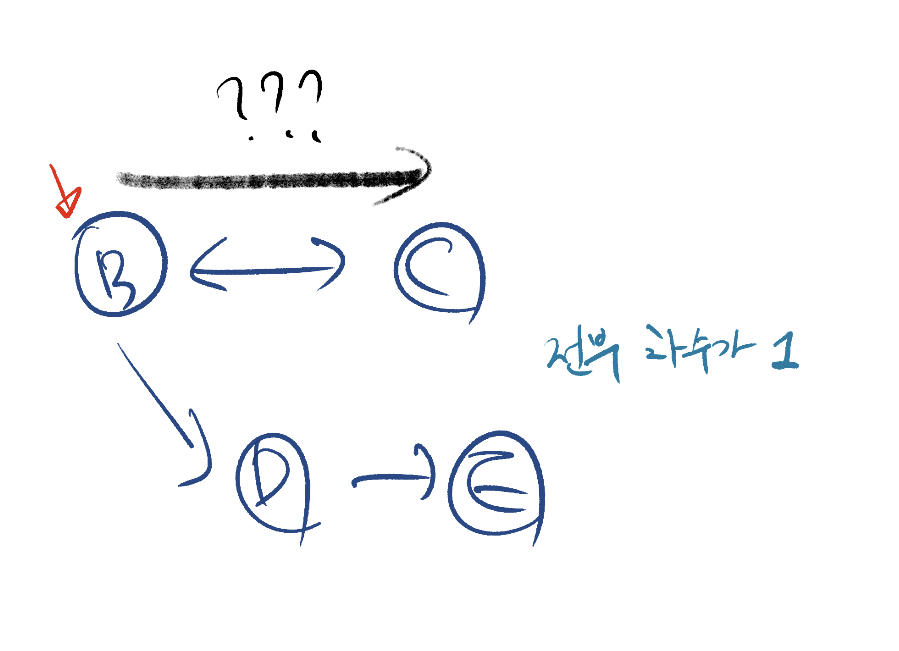
이제 이 그래프에서 진입 차수가 0인 노드를 찾아야 하는데, 노드 B, C, D는 전부 차수가 1이므로 차수가 0인 노드를 찾을 수 없고 더 이상의 진행을 할 수 없습니다. 위상 정렬은 주어진 그래프가 DAG인 경우만 가능하는 점에서 보면, 탐색하는 그래프 내에 적어도 한개 이상의 사이클이 있다는 것이 확인됩니다. 즉, 노드 A만 방문했지만 그래프 어딘가에 사이클이 있다는 것이 판단 가능하죠. 물론 이 예시는 상당히 간소화 된 그래프이기 때문에 좀 극단적이긴 합니다.

하지만, BFS 방식은 노드 A에서 출발해 직접 연결된 노드를 우선적으로 탐색합니다. 그리고 방문한 노드는 방문 리스트에 추가합니다. 아무튼 그 다음에 노드 B를 방문하고, 노드 B와 연결된 노드 C를 방문합니다. 이제 노드 C에 연결된 노드 B를 방문하는데, 이 경우 노드 B는 이미 방문 리스트에 있으므로 사이클이 있음을 탐지하게 됩니다. 하지만, 이 경우 적어도 노드 A, B, C는 방문해야 하기 때문에 위상 정렬 보다는 시간이 더 걸리게 됩니다.

마무리

이것으로 액터 시스템 내부에 구독 관계를 추가할 때 미리 사이클이 있는지 판별하는 알고리즘을 작성해봤습니다. BFS, DFS 그리고 위상 정렬을 비교해보면서 왜 이런 결과가 나오게 됐는지 분석도 해봤습니다. 물론 벤치마크에서 사용한 그래프는 간략한 구조를 가졌기 때문에 실제 액터 모델에서 돌리면 또 다른 결과가 나올 것입니다. 하지만, 대부분의 경우 위상 정렬이 BFS, DFS 보다 효율적일 것이라고 생각합니다. 왜냐하면, 그래프 전체를 스캔하는 것이 아닌 특정 액터(노드)에서 시작하는 구독 관계에서 사이클이 있는지 판단하는 것이기 때문에 여기서 사용한 예시와 크게 다르지 않을 것이기 때문입니다.

---

참고문서

1. <Introduction to Algorithms (3rd edition)> (cormen et al., MIT press, pp.594-615)