소유권 그래프
러스트의 소유권(ownership)은 변수가 가리키는 값을 한번에 하나만 소유할 수 있도록 하여 메모리 안정성을 보장하는 시스템입니다. 이번 글에서는 이 소유권의 개념을 직접 만들고 있는 언어에 어떻게 적용하고 있는지 풀어보겠습니다.
빌림 (Borrowing)
소유권 그래프를 구현하기에 앞서 빌림과 소유권에 대해 알아보겠습니다. 먼저 러스트의 빌림 규칙은 소유권(ownership)과 참조(reference) 그리고 빌림(borrowing)을 기반으로 작동합니다.
- 소유권: 이후에 설명하겠지만, 러스트에서 값은 항상 한 번에 하나의 소유자(owner)를 가질 수 있습니다. 소유자는 값에 대한 제어권을 가지고, 해당 값이 스코프를 벗어나면,
drop을 통해 자동으로 메모리에서 해제됩니다. - 참조: 또한 빌림을 이용해 값에 대한 참조자(reference)를 생성할 수 있습니다. 참조자는 값을 소유하지 않고도 값을 읽거나 변경할 수 있습니다. 참조자는 불변 참조자(immutable reference)와 가변 참조자(mutable reference)로 나뉘며, 불변 참조자는 여러 개의 동시 참조를 허용하지만 가변 참조자는 오직 하나의 동시 참조만 허용합니다.
- 빌림: 소유자가 값을 임시로 다른 코드 블럭에 대여할 수 있습니다. 이러면 소유권을 넘기지 않고도 값을 사용할 수 있습니다. 빌림은 동시에 여러 개의 불변 빌림(immutable borrowing)이 가능하지만, 가변 빌림(mutable borrowing)은 하나의 빌림만 허용합니다.
소유권 (Ownership)
소유권에 대해 간단히 알아보겠습니다. 러스트의 소유권은 객체(값)의 소유권을 추적하고 객체가 더 이상 필요하지 않을 때 해제하는 식으로 동작합니다. 이때 각각의 객체에 대한 소유권은 오직 하나의 소유자만 가질 수 있고, 소유권을 가진 객체가 소멸하면 자동으로 메모리를 해제합니다. 이로써 가비지 컬렉터 없이 메모리 안정성을 보장합니다.
소유권을 다른 변수에 할당하려면 값을 이동(move)해야 하는데, 값을 이동하면 소유권이 새로운 변수로 이동합니다. 하지만 이존 변수의 소유권은 무효화됩니다.
또한 복사(copy)는 데이터를 복사해서 새로운 소유자를 생성합니다. 소유권을 가진 변수를 다른 변수에 할당하면 해당 데이터의 복사본이 새로운 메모리 공간에 할당됩니다. 이 복사된 데이터는 원본 데이터와는 독립적으로 존재하며, 각 변수는 서로 다른 소유권을 가집니다.
하지만 복사의 비용은 비싸기 때문에 참조(reference)를 하는 방법도 있습니다. 참조자를 사용하면 객체에 대한 접근을 공유할 수 있는데, 참조자는 객체를 소유하지 않고 단순히 참조만을 제공합니다. 이를 통해 여러 개의 참조자가 동시에 데이터에 접근할 수 있게됩니다.
소유권 그래프 (Ownership Graph)
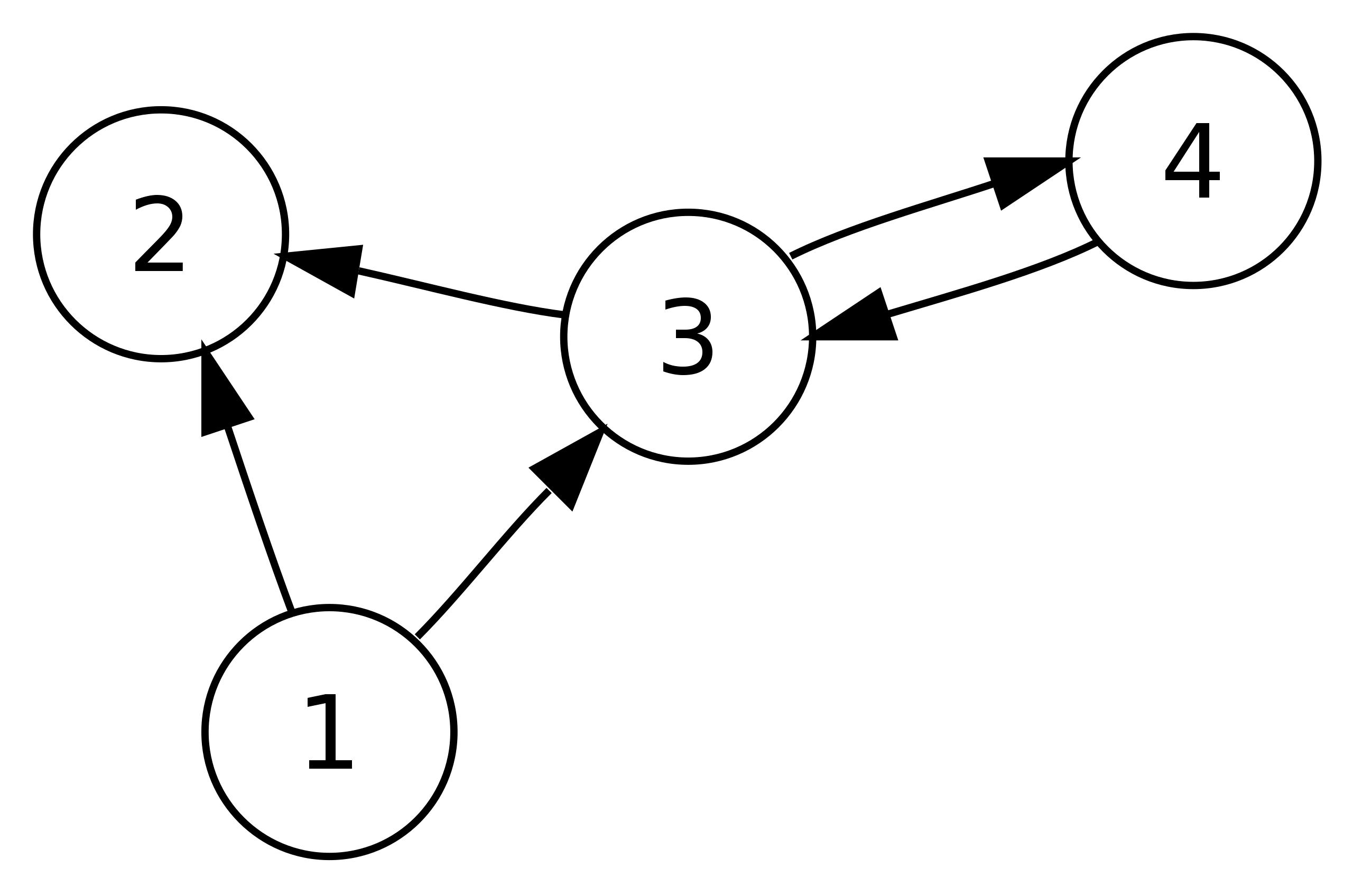
유향 그래프 구조를 간단히 묘사한 그림. 3번, 4번 노드는 서로 연결되어 있고, 3번 노드는 2번을 그리고 1번 노드는 2번, 3번 노드를 향하고 있다.
그렇다면 이 소유권을 추적하기 위해선 어떻게 해야할까요? 정적 분석(Static Analysis)이나 참조 계수(Reference counting)를 이용할 수 있고, 아니면 Garbage Colletion과 같은 방법도 있습니다. 하지만 여기서는 소유권 그래프를 구현한 뒤, 소유권을 추적해보겠습니다.
그래프를 이용하면 컴파일 시간에 소유권 규칙을 검사할 수 있고, 코드의 소유권 이동과 참조자의 범위를 깔끔하게 처리할 수 있습니다. 또한, 추가 오버헤드가 발생하지 않아 리소스나 시간을 효율적으로 유지할 수 있게 도와줍니다.
그래프는 소유권과 빌림(borrowing)의 관계를 보여줍니다. 그래프의 노드(node)는 변수 또는 객체를 나타내며, 간선(edge)은 소유권의 이동이나 참조 관계를 의미합니다. 그래프는 변수의 선언이나 할당이 이뤄질때 생성되고, 변수의 소유권은 노드 간의 연결로 나타냅니다.
예를 들어, 변수의 소유권을 다른 변수로 넘겨주면, 그래프에는 소유권 이동을 표시하는 간선이 추가됩니다. 이때 소유권 이동은 이전 변수의 무효화와 새로운 변수의 소유권 취득을 의미합니다.
참조자의 생성과 사용은 그래프에서 참조 관계를 나타냅니다. 참조자는 소유권을 가지지 않고 객체에 대한 접근을 제공하기 때문에 그래프에는 참조자를 의미하는 간선이 형성됩니다. 추가로 이 참조자는 소유권의 범위 내에서만 유효합니다.
컴파일러는 소유권 그래프를 정적으로 검사하고 규칙을 잘 지키고 있는지 확인합니다. 러스트를 예로 들면, 불변 참조자와 가변 참조자 간의 충돌이나 그외 다른 문제들도 컴파일 시간에 분석해 문제를 미연에 방지합니다.
더 깊고 자세한 내용은 딴 블로그나 공식문서를 확인하는게 더 이로울 것 같으니 넘어가겠습니다. 또한 여기서 구현할 코드는 위에서 말한 복잡한 내용들을 전부 쳐낸 열화-열화판으로 구현할 것입니다.
소유권 그래프 구현
소유권 그래프를 구현하기 전에 어떻게 구현하고 또 어떤 데이터 구조를 사용해야 할까요? 먼저 소유권 그래프의 작동 방식을 보겠습니다.
작동 방식
각 단계를 단순하게 표현하면 다음과 같습니다.
- AST(추상 구문 트리)를 순회하면서 각각의 스코프 노드를 만날 때마다 새로운 스코프를 생성합니다.
- 각 스코프는 변수의 소유권을 추적하기 위한 변수 테이블(인접성 목록)을 유지합니다.
- 변수가 생성될 때, 현재 스코프에 소유권 정보를 등록합니다.
- 빌림이 발생할 때, 변수가 다른 스코프에 이미 빌려져 있는지 확인합니다..
- 빌림이 발생하면 해당 노드의 연결 목록에 변수의 차용 정보를 추가합니다.
- 범위가 끝나면 연결 목록에서 변수의 빌림 정보를 제거합니다.
- 중첩된 범위에서 빌림이 발생하는 경우, 각각의 범위에서 빌림을 해결하고 소유권 정보를 업데이트합니다.
- AST 순회가 완료된 후, 모든 빌림 규칙을 확인하여 빌림이 올바른지 확인합니다.
이제 각 단계에 해당하는 코드를 보면서 어떤 걸 고려하고 또 어떻게 작동하는지 알아보겠습니다. 다만 중첩 스코프의 경우는 아직 완전히 구현되지 않아 추정되는 동작만을 서술했다는 점은 양해부탁드립니다. 또한 아래의 코드 스니펫(snippet)은 별다른 설명이 없다면 build_ownership_graph 메서드 내에 있는 부분입니다.
AST 순회 및 새 스코프 생성
현재 언어 구현하고 있는 언어에는 AST를 아래와 같이 정의합니다. 자세한 설명이나 다른 부분은 생략했지만 이 링크에서 전체 코드를 확인할 수 있습니다.
// borrows/ast.rs
#[derive(Debug, PartialEq)]
pub enum Statement {
FunctionDef {
name: String,
args: Option<Vec<(String, bool)>>,
body: Vec<Statement>,
},
VariableDecl {
name: String,
value: Option<Expression>,
is_borrowed: bool,
},
Scope(Vec<Statement>),
Return(Option<Expression>),
Expr(Expression),
}
// ...아래의 코드는 AST는 순회하면서 Statement::Scope(_) 노드를 만날 때마다 새로운 스코프를 생성하는 부분입니다.
// borrow/ownership.rs
Statement::Scope(scope) => {
let prev_owner = current_owner.clone();
let mut declared_in_scope = vec![];
for inner_stmt in scope {
// ...
}
// ...
}prev_owner는 이전 소유자를 저장하고, current_owner는 현재 소유자를 저장합니다. 또한 declared_in_scope 변수는 현재 스코프에서 저장된 변수들을 저장하는 역할을 합니다.
각 스코프의 변수 테이블
소유권 그래프의 구현에는 인접 리스트(Adjacency List), 인접 행렬(Adjacency Matrix) 아니면 둘 다 결합한 인접 리스트 배열(Adjacency List Array)과 같은 여러가지 데이터 구조들을 사용할 수 있습니다. 아래의 표는 이 세가지 데이터 구조를 비교한 표입니다. 여기서 는 정점의 수를, 는 간선의 개수의 의미합니다.
| 인접 리스트 | 인접 배열 | 인접 리스트 배열 | |
|---|---|---|---|
| 복잡도 | |||
| 노드 추가 | |||
| 노드 삭제 [deg] | |||
| 노드 탐색 | |||
| 희소 그래프 | 효율적 | 비효율적 | 효율적 |
| 밀집 그래프 | 비효율적 | 효율적 | 효율적 |
| 노드 연결 정보 저장 | 연결 리스트 | 2차원 배열 | 연결 리스트 |
| 메모리 사용량 | 중간 | 높음 | 중간 |
인접 리스트는 각 노드마다 인접한 노드들의 연결 리스트를 가지고 있으므로 저장 공간이 노드 수와 간선 수에 비례합니다. 노드 추가와 삭제가 용이하며, 노드 탐색에는 의 시간 복잡도를 가지는 것을 볼 수 있습니다. 또한 표에는 안 나와있지만 추가 정보를 저장하기에도 용이한 구조입니다.
하지만 밀집 그래프에서는 비효율적인데, 현재 만들고 있는 언어는 테스트 용으로 쓰기 좋게 최소한의 구조와 기능만을 가지도록 만들고 있어서 밀집된 경우는 굳이 고려하지 않아도 됩니다. 그래서 그래프 구현에는 인접 리스트 방식을 사용할 것입니다.
이제 그래프의 구조와 관계를 어떻게 표현했는지 알아보겠습니다. 먼저, 노드의 연결 정보는 연결 리스트를 통해 저장합니다. 각 노드는 인접한 노드들을 연결 리스트로 저장하며, 이를 통해 그래프의 구조를 나타냅니다.
처음 구현을 시도했을 때 사용했던 자료구조는 해시 맵(HashMap)이였습니다. 하지만 아래의 결과에서 보이듯 생각과 다르게 동작했다는 문제점이 발생했습니다.
// borrow/ownership.rs [예전 구현]
#[derive(Debug, PartialEq, Eq, Clone)]
struct OwnershipGraph {
graph: HashMap<String, Vec<String>>, // 해시 맵을 이용해 그래프 구조 생성
}
impl OwnershipGraph {
pub fn new() -> Self {
graph: HashMap::new(),
}
}예를 들어 다음과 같은 AST가 입력으로 들어갔다고 가정하면,
// let a = 42;
// let b = &a;
// let c = &a;
// let d = &b;
**[AST]**
Statement::VariableDecl {
name: "a".into(),
is_borrowed: false,
value: Some(Expression::Number(42)),
},
Statement::VariableDecl {
name: "b".into(),
is_borrowed: true,
value: Some(Expression::Reference("a")),
},
Statement::VariableDecl {
name: "c".into(),
is_borrowed: true,
value: Some(Expression::Reference("a")),
},
Statement::VariableDecl {
name: "d".into(),
is_borrowed: true,
value: Some(Expression::Reference("b")),
}다음과 같은 결과가 나와야 합니다.
OwnershipGraph { graph: {"a": ["b", "c"], "b": ["d"], "global_var": ["a"]} }하지만 아래와 같은 결과가 출력되었죠.
OwnershipGraph { graph: {"a": ["c", "d"], "b": [""], "global_var": ["a"]} }처음에는 원인을 알 수 없었지만, 이후 분석해보니, 해시 맵 특성상 순서가 뒤죽박죽 저장되어서 소유권의 관계를 정확하게 추적하지 못해서 발생한 문제였었습니다. 그래서 순서를 유지하면서 그래프 관계를 만들 수 있는 자료구조로 변경해야 될 필요가 생겼습니다.
그래서 해시 맵 대신 B-트리 맵(BTreeMap)으로 코드를 수정했습니다. 해시 맵에 비해 상대적으로 연산은 좀 걸리지만[BTM], 키(각 변수 노드)를 기준으로 정렬된 상태를 유지하기 때문에 소유권의 전파와 전이를 파악하는데 적합했습니다.
그렇다면 정렬된 순서를 왜 유지해야 할까요? 바로 이 순서를 유지해야 소유권 관계의 시간적 흐름을 명징하게 처리할 수 있기 때문입니다.
예를 들어, 소유권 이전과 이후를 비교하거나, 특정 시간 범위 내에서 소유권 관계를 탐색해야한다고 가정해봅시다. 만약 이때 해시 맵을 사용한다면 큰 어려움이 발생합니다.
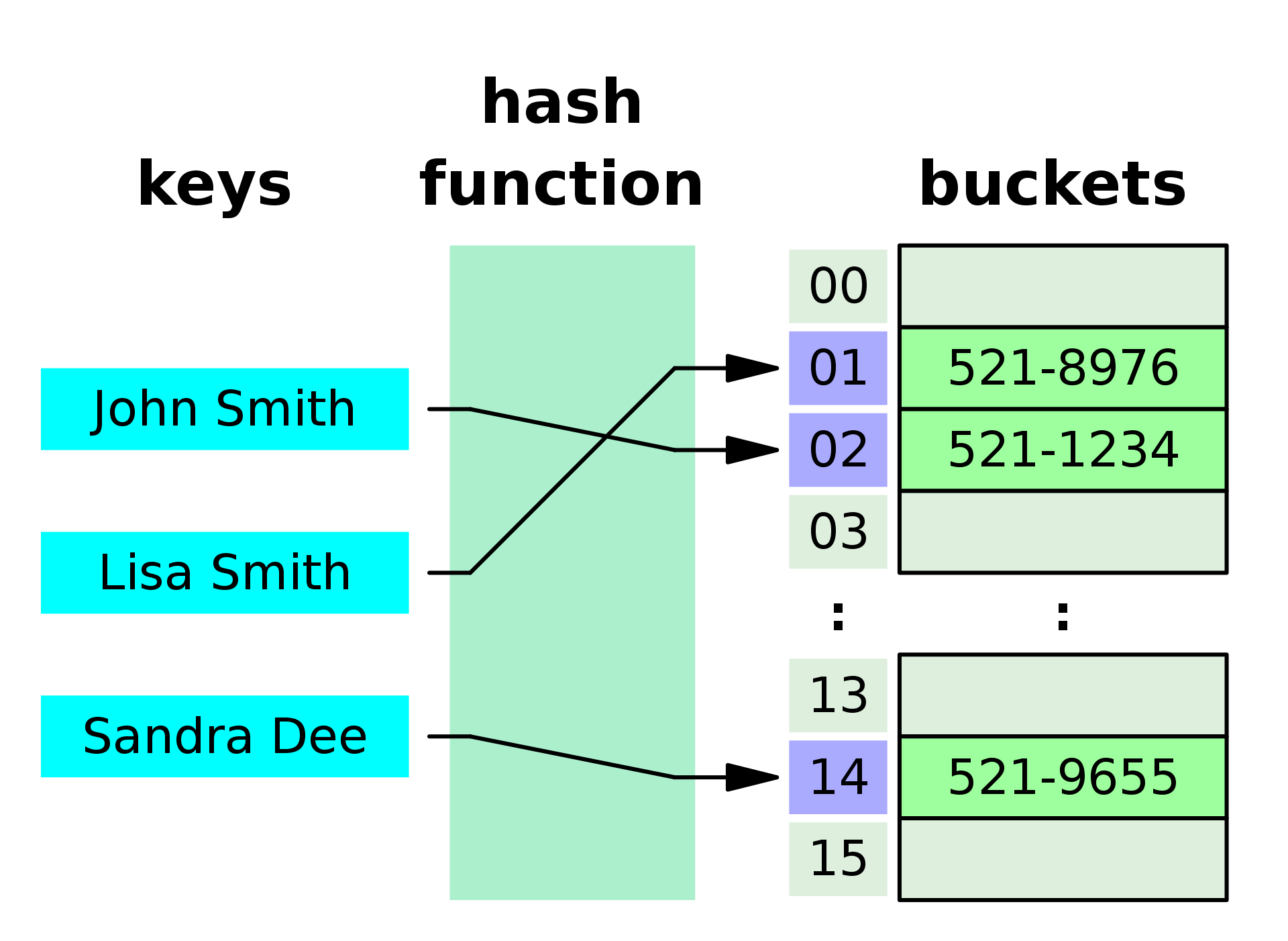
해시 맵이 어떤 식으로 동작하는지 묘사한 그림. 각 키에 해당하는 값들이 해시 함수를 통과해 특정 값을 가지는지 묘사되어 있다.
왜냐하면 해시 맵은 해시 함수를 이용하여 키를 해시 값으로 변환한 후 데이터에 접근하기 때문에 키-값(key-value)이 정렬되는 순서를 예측할 수 없기 때문이죠. 또한 연속된 범위(특정 시간) 내에서 소유권 관계를 탐색하려면 일련의 키-값 순서대로 탐색을 하는 것이 아닌 해시 맵을 순회하면서 범위를 검사해야 하는 것도 덤입니다.
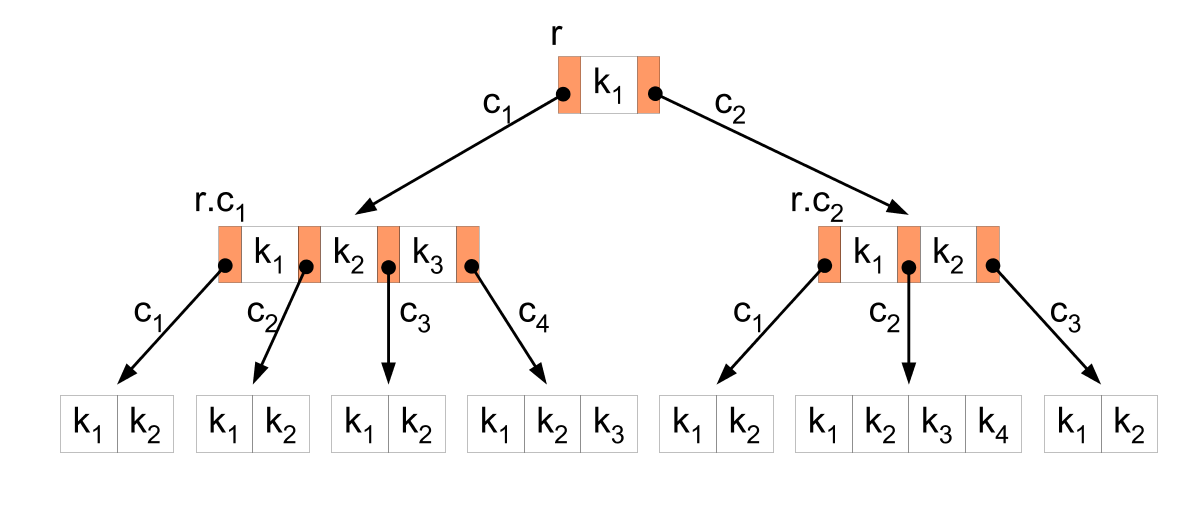
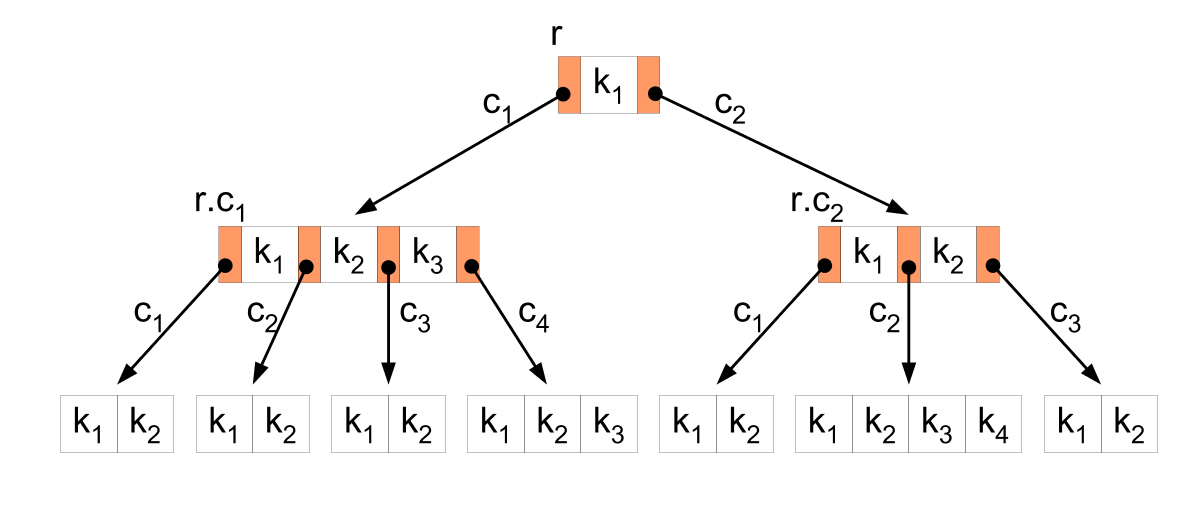
B트리가 어떤 식으로 동작하는지 묘사되있는 그림이다. 를 루트로 하여 순서대로 정렬된 구조를 가진다.
반면, B 트리 맵은 키를 기준으로 정렬된 상태를 유지하는 자료구조입니다. 각 노드를 키로 하고 인접 리스트를 값으로 저장하면, B트리는 키의 정렬된 순서를 유지하면서 소유권 관계를 저장합니다.그렇기 때문에 소유권의 이전과 이후, 또는 특정 시간 범위 내에서 소유권 관계를 탐색할 때 용이합니다.
B트리 맵으로 표현한 그래프 구조는 아래와 같습니다.
// borrow/ownership.rs
#[derive(Debug, PartialEq, Eq, Clone)]
struct OwnershipGraph {
graph: BTreeMap<String, Vec<String>>,
}각 키(String)는 그래프의 노드를, 해당 키에 연결된 값(Vec<String>)은 해당 노드에 인접한 노드들을 표현한 인접 리스트입니다. 그래프의 구조는 소유권 그래프 문단을 확인해주세요.
이 그래프는 OwnershipGraph::new 메서드를 통해 생성됩니다.
impl OwnershipGraph {
pub fn new() -> Self {
graph: BTreeMap::new(),
}
}이제 테스트를 실행시켜보면 의도한 그래프의 형태를 가지게 되었다는 것을 확인할 수 있습니다.
소유권 등록
// borrow/ownership.rs
const GLOBAL: &str = "global_var"; // <- 전역(global) 스코프를 나타냅니다
//...
Statement::VariableDecl { name, is_borrowed, value } => {
if *is_borrowed {
if let Some(Expression::Reference(ref_var)) = value {
current_owner = ref_var.clone();
graph.add_borrower(¤t_owner, name); // <- 소유권 등록
}
} else { // -+ 변수에 할당된 값이 어떤 변수를
current_owner = GLOBAL.to_string(); // | 참조한 경우가 아니면, 해당 스코프의
} // -+ 전역 변수로 처리.
graph.add_owner(¤t_owner, name);
}
// ...변수가 선언되면 그 변수의 소유권을 현재 스코프에 등록합니다. OwnershipGraph::add_owner 메서드를 사용하여 현재 소유자(current_owner)를 변수의 소유자 목록에 추가합니다.
else 구문 내부에서는 스코프 내의 변수의 값이 참조된게 아니면 그 스코프 내에서의 전역 변수로 처리하도록 합니다.
impl OwnershipGraph {
fn add_owner(&mut self, owner: &str, variable: &str) {
let entry = self.graph.entry(owner.to_string()).or_insert_with(Vec::new);
if !entry.contains(&variable.to_string()) {
entry.push(variable.to_string());
}
}위에서 보이듯 이 메서드는 그래프에 새로운 노드(owner)를 추가합니다. 새로운 변수가 선언될 때 노드가 추가됩니다.
빌림 검사
// borrow/ownership.rs
// ...
if *is_borrowed {
if let Some(Expression::Reference(ref_var)) = value {
current_owner = ref_var.clone(); // <- 1
// ...
}
}이 코드는 변수가 참조되는 경우를 처리합니다. is_borrowed가 참인 경우, 즉 변수가 별려지는 경우에 이 코드 블록이 실행됩니다.
value가 Expression::Reference 타입인 경우는 차용되는 변수가 참조(Reference) 되고 있음을 나타냅니다. ref_var는 참조되는 변수의 이름을 가리킵니다.
(1)에서 차용되는 변수(ref_var)를 현재 소유자(current_owner)로 설정합니다. 이는 차용되는 변수가 다른 스코프에 이미 소유되어 있는지 확인하는 과정입니다. 만약 ref_var가 이미 다른 스코프에 소유되어 있다면, 그 스코프가 현재 소유자가 됩니다.
이 과정을 통해, 변수가 빌려지는 경우 해당 변수가 이미 다른 스코프에 소유되어 있는지 확인하고, 그 스코프를 현재 소유자로 설정하여 빌림을 관리합니다. 이는 러스트의 소유권 및 빌림 규칙을 모방한 것으로, 한 번에 하나의 소유자만을 가질 수 있고, 불변 참조는 여러 개 있을 수 있지만 가변 참조는 한 번에 하나만 있어야 한다는 규칙을 지키도록 합니다.
대여 리스트 업데이트
// borrow/ownership.rs
if *is_borrowed {
if let Some(Expression::Reference(ref_var)) = value {
current_owner = ref_var.clone();
graph.add_borrower(¤t_owner, name); // <-
}
}변수가 참조되는 경우, 그 빌림을 노드의 대여 목록에 추가합니다. OwnershipGraph::add_borrower 메서드를 사용하여 현재 소유자(current_owner)를 변수의 대여 목록에 추가합니다.
impl OwnershipGraph {
pub fn add_borrower(&mut self, owner: &str, borrower: &str) {
if let Some(borrowers) = self.graph.get_mut(owner) {
if !borrowers.contains(&borrower.to_string()) {
borrowers.push(borrower.to_string());
}
}
}
}OwnershipGraph::add_borrower는 그래프의 노드 사이에 간선을 추가합니다. 변수가 다른 변수로부터 참조되면 간선이 추가됩니다.
빌림 제거
// borrow/ownership.rs
for var in declared_in_scope {
graph.remove_owner(&prev_owner, &var);
current_owner = prev_owner.clone();
}차용 범위가 끝나면, 그 범위에서 선언된 모든 변수의 빌림을 연결 목록에서 제거합니다. OwnershipGraph:remove_owner 메서드를 사용하여 이전 소유자(prev_owner)를 변수의 소유자 목록에서 제거합니다.
impl OwnershipGraph {
pub fn remove_owner(&mut self, owner: &str, variable: &str) {
if let Some(owners) = self.graph.get_mut(owner) {
owners.retain(|x| x != variable);
}
}
}이 메서드는 그래프에서 노드(owner)를 제거합니다. 변수가 범위를 벗어날 때 노드가 제거됩니다.
소유권 정보 업데이트
⚠️ 이 부분은 아직 스코프가 완전히 구현되지 않아 예상되는 대략적인 동작만을 설명합니다. 하지만 추후 업데이트 될 예정입니다. [2023-06-12 기준]
// borrow/ownership.rs
Statement::Scope(scope) => {
let prev_owner = current_owner.clone();
let mut declared_in_scope = vec![]; // <- 1
for inner_stmt in scope {
if let Statement::VariableDecl { name, value, is_borrowed } = inner_stmt {
declared_in_scope.push(name.clone());
// ...
graph.add_owner(&prev_owner, name); // <- 2
current_owner = name.clone(); // <- 3
}
}
// ...
}중첩된 범위에서 빌림이 발생하는 경우, 각 범위에서 빌림을 적절히 해결하고 소유권 정보를 업데이트합니다. 이 코드는 중첩된 범위에서 변수를 선언하고(1), 그 변수의 소유권을 이전 소유자(prev_owner)에 등록하며(2), 변수를 현재 소유자(current_owner)로 설정(3)하는 과정을 보여줍니다.
최종 빌림 규칙 검사
// borrow/ownership.rs
for (variable, owners) in &graph.graph {
if owners.len() > 1 { // <- 1
for owner in owners { // <- 2
if owner == variable { // <- 3
return Err(OwnerGraphError::MultipleOwners(variable.clone()));
}
}
}
}이 코드는 AST 순회가 끝난 후 모든 빌림 규칙을 확인하여 빌림이 올바른지 확인하는 부분입니다.
(1)에서는 한 변수가 여러 소유자를 가지고 있는지 확인합니다. 소유권 규칙에서 변수는 한 번에 하나의 소유자만을 가질 수 있기 때문입니다.
(2)에서는 소유자 목록의 각 소유자에 대해 검사를 적용합니다.
(3)에서는 소유자가 변수 자신을 소유하고 있는지 확인합니다. 이는 변수가 자기 자신을 소유하고 있는지 확인하는 것으로, 이 경우에도 빌림 규칙을 위반한 것입니다.
즉, AST 순회를 마친 뒤, 빌림 규칙을 적용하여 올바르게 빌렸는지 검증하는 단계입니다. 만약 한 변수가 여러 소유자를 가지고 있거나, 자기 자신을 소유하는 경우에는 MultipleOwners 에러를 반환합니다.
전체 코드
전체 구현 코드는 다음 링크를 참고해주세요. 소유권 그래프 뿐만 아니라 현재 구현된 AST나 파서와 같은 부분들도 볼 수 있습니다. [구현]
마무리
이것으로 소유권 그래프의 구현과 설명을 마치겠습니다. 먼저 러스트의 빌림 규칙과 소유권에 대해 간단히 알아보았고, 그래프를 구현하는 과정에서 고려해야 할 사항과 데이터 구조, 그리고 정렬된 상태로 유지해야 하는 이유 등을 살펴보았습니다. 아직 완벽하게 동작하는 코드는 아니지만(작성 시점 기준으로), 이런 대략적인 흐름을 파악하고 구현하는 데 참고가 되었으면 좋겠습니다.
각주
[deg] 그래프 이론에서 는 정점(vertex)의 차수(degree)를 의미합니다. 즉, 정점 에 접하는 간선(edge)의 수를 나타냅니다. 는 일반적으로 정점 v의 차수에 따라 달라지는 일부 알고리즘 또는 연산에 대한 시간 복잡성의 상한을 나타내며, 이는 시간 복잡성이 최대 의 일정한 배수에 비례한다는 의미입니다.
인접 리스트의 노드 삭제의 복잡도는 로 표기할 수 있지만, 소유권 그래프에서 노드 삭제는 해당 노드와 연결된 모든 소유권 관계를 수정해야 하기 때문에 연결된 간선의 차수에 따라 소요 시간이 달라집니다. 따라서 이 표에서는 삭제에 걸리는 복잡도를 로 표현했습니다. 이는 인접 리스트 배열의 노드 삭제에도 해당됩니다.
[BTM] BTreeMap에서 노드 삭제, 삽입, 검색의 복잡도는 입니다. HashMap의 에 비하면 느리지만, 딱히 신경 쓸 필요는 없습니다.