파이썬 기초수학

매생이·2021년 10월 12일

python 기초수학

파이썬 공부

목록 보기

4/8

기초수학

약수 : 어떤 수를 나누어 떨어지게 하는 수.
예시 : 21의 약수는 1, 3, 7, 21 이다.

소수 : 1과 자기자신 외의 약수가 존재하지 않는 수
예시 : 13의 약수는 1, 13 이므로 소수이다.

소수를 찾는 알고리즘
소수를 찾으려고 일일히 소인수 분해를 하는데에는 시간이 굉장히 오래걸릴 수 있다.
이러한 경우를 위해 코드로 구현할 수 있는 알고리즘이 존재하는데, 바로 에라토스테네스의 체 라는 알고리즘이다.
예시로, 100이하의 소수를 찾기 위해서 100의 제곱근인 10까지의 숫자들의 100이하의 배수들을 제거해나가면, 소수만 남는다는 이론이다.

소인수 : 약수이면서 소수인 숫자를 부르는 말.
소인수 분해 : 합성수를 소인수들의 곱으로 표현하는 것.

n = int(input("소인수분해할 수를 입력하세요 : "))
i = 2
numbers = []
while i<=n:
  if n%i==0:
    numbers.append(i)
    n/=i
  else:
    i+=1
num = 1
for j in numbers:
  num*=j
print("숫자 : ", num)
print("소인수 목록 : ", numbers)

실행결과 :
소인수분해할 수를 입력하세요 : 72
숫자 : 72
소인수 목록 : [2, 2, 2, 3, 3]

최대 공약수 : 두 합성수가 함께 가지는 가장 큰 약수.

최대공약수를 구하기 위해서는 두 수가 가지는 약수들 중에서 겹치는 약수를 확인하고 그 중에서 가장 큰 수를 골라야한다.
하지만 그러지 않고 더 쉽게 구하는 방법이 있다.

유클리드 호제법 : 기원전의 수학자 유클리드가 고안한 방법으로, a와 b의 최대공약수를 구할 때, a를 b로 나눈 나머지를 c라고 하고. b를 c로 나눴을 때 나머지를 구하여 다시 연산하는 재귀함수를 G(a,b)라고 할때, 나머지가 0이 될때까지 반복하여 0이 되었을 경우의 b가 최대공약수이다.

#유클리드 호제법

def uclide_method(a,b):
  temp = a%b
  if temp==0:
    return b
  else:
    return uclide_method(b,temp)

a= 2304
b= 1440

uclide_method(a,b)

실행결과 : 288

최소 공배수 : 두 수의 배수들 중에서 겹치는 수 중에 가장 작은 배수

최소 공배수도 최대 공약수를 응용해서 구하면 쉽게 구할 수 있다.

a와 b의 최대 공약수를 구한 뒤, a와b를 곱한 후 최대 공약수로 나누었을때, 나머지를 제외한 몫이 바로 최소 공배수이다.

a=int(input("a를 입력해주세요 : "))
b=int(input("b를 입력해주세요 : "))

c=uclide_method(a,b)

print("a와 b의 최대 공배수 : ",int(a*b/c))
실행 결과 :
a를 입력해주세요 : 18
b를 입력해주세요 : 12
최대 공배수 : 36

3개의 숫자의 최대 공배수를 구할때도 이 방법으로 먼저 두개의 최대공배수를 구하고, 그 최대 공배수와 세번째 수의 최대공배수를 구하면 된다.

진법

진법 : 특정 숫자 몇개를 사용하여 수를 표시하는 방법이다.

2진법 : 0과1
8진법 : 0~7
10진법 : 0~9
16진수 : 0~9,(A:10,B:11,C:12,D:13,E:14,F:15)

10진수를 n진수로 바꾸는 방법

2진수
기존의 10진수 값을 2로 나누어서 나머지가 0이면 0 1이면 1을 적고 왼쪽칸에서 나눠진 값을 다시 2로 나누는 것을 반복하면 된다.
ex) 14 => 14/2 = 몫 7 나머지 0 (0), 7/2 = 몫3 나머지1 (10), 3/2 = 몫1 나머지1 (110), 1/2 = 몫0 나머지1 (1110).
8진수
기존 10진수 값을 8로 나눌 수 없을 때까지 나누어서 몫과 나머지를 붙여주면 된다.
ex) 35 => 35/8 = 몫4 나머지 3 (43). 다시 변환해보면 4(8의1승) + 3(8의0승)
= 35가 된다.
16진수
기존 10진수 값을 16으로 나눌 수 없을 때까지 나누어서 몫과 나머지를 붙여주면 된다.
ex) 56 => 56/16 = 몫3 나머지8 (38).
이것도 다시 변환해보면 3*(16의1승)+8(16의0승) = 56 임을 알 수 있다.

n진법으로 표현된 숫자를 쉽게 읽는 방법은 오른쪽 숫자부터 한자리씩 n의0승부터 1승씩 올려가며 계산하면 10진수로 이해할 수 있다.

2진수에서 8진수 변환
n진수에서 m진수로 변환할 때의 키포인트는, n과 m의 관계이다.
8은 2의 3승이기 때문에 2진법의 3자리수만큼이 8진수의 1자리수만큼을 표현할 수 있다.
그래서 2진수를 8진수로 변환하려면 맨 뒤에서부터 3자리씩 끊어서 표현하여야한다.
(3으로 안나누어지면 맨앞에 0을 더 덧붙여주면 된다.)
ex)

1010100 -> 1 010 100(3자리로 안나누어져서 맨 앞에 한자리가 남았으므로 0을 덧붙여준다) -> 001 010 100.
이렇게 자리를 나누어준 후에 3자리가 각각의 2진수라고 생각하고 10진수로 바꾸어주면 1, 2, 4가 된다.
이를 이어붙이면 8진수 124가 된다.
$124 = 1*(8^2) + 2*(8^1) + 4*(8^0)$ = 10진수 84.
2진수 1010100 = $1*(2^6) + 0*(2^5) + 1 * (2^4) + 0 * (2^3) + 1 * (2^2) + 0 * (2^1) + 0 * (2^0) = 64 + 16 + 4$ = 10진수 84

#10진수와 2진수 변환 예시 코드
n = 30
binary = []
#2진수로 변환
while (1):
  binary.append(n%2)
  if((n/2)>=1):
    n=int(n/2)
  else:
    break
binary = binary[::-1]
#문자열을 뒤집어주는 방법
num=0
#10진수로 다시 변환
for i in range(len(binary)):
  if(binary[i]==1):
    num +=2**(i+1)
print(num," = ",binary)

실행결과 :
30 = [1, 1, 1, 1, 0]

수열

수열이란 ? 규칙성을 가지고 나열되어있는 수들

ex)
[2, 4, 6, 8, 10, 12, 14, 16.......x]
$[a_1, a_2, a_3, a_4, a_5, a_6, a_7, a_8.......a_n]$
a의n번째항 = 일반항

첫번째 항에 특정한 차이를 더하거나 곱하면 다른 일반항을 찾을 수 있다.

위에 같은 경우는 $a_n = a_1+(n-1)*2$ 로 구할 수 있다.

등차수열 : 연속된 두 항의 차이가 일정한 수열. 등차 수열의 규칙성을 이용해서 일반항을 구할 수 있다.

등차수열의 합 : 규칙성을 이용해서 모든 항들의 총합을 구할 수 있다.
일반항 = $a_n = a_1 + (n-1)*d$ (d는 두 항사이의 차이) 이므로,
$S_n = a_1+ a_2 + a_3 + ..... + a_n = n(2(a_1) + (n-1)*d) = n(2a_1 + (n-1)*d)/2 = n(a_1+a_n)/2$ 와 같다.

#수열을 보고 n번째 항까지의 합을 출력하는 프로그램

a1 = 3
dist = 5
n = 8
i=1
list = []
sum=0
while i<=n:
  print(i,"번째 항 : ",a1+(i-1)*(dist))
  list.append(a1+(i-1)*(dist))
  sum+=a1+(i-1)*(dist)
  i+=1

print(n,"번째 항까지의 합 : ",sum)

sum2 = n*(a1+a1+(n-1)*dist)/2
sum2
실행결과 :
1 번째 항 : 3
2 번째 항 : 8
3 번째 항 : 13
4 번째 항 : 18
5 번째 항 : 23
6 번째 항 : 28
7 번째 항 : 33
8 번째 항 : 38
8 번째 항까지의 합 : 164
164.0

등비 수열
등비 수열이란 연속된 두 항의 비가 일정한 수열이다.
an = $a1*(r^(n-1))$ (r은 두 항의 비, 공비라고 부른다)

등비수열 또한 규칙성을 이용해서 모든 항들의 총합을 구할 수 있다.
Sn = $(a_1*r^0)-(a_1*r^(n))$ -> $(a_1*r^0)-(a_1*r^n)/(1-r)$
-> $a_1*(1-(r^n))/(1-r)$

등비중항 : 두 일반항 사이 중간항의 값. $a_n * a_(n+2) = (a_n+1)^2 -> sqrt(a_(n+1)) -> a_(n+1)$

a1 =5
r = 3
n=7

print(n,"번째 항의 값 : ",a1*(r**(n-1)))
list = []
sum=0
i=1
while i <= n:
  print(i,"번째 항 : ",a1*(r**(i-1)))
  list.append(a1*(r**(i-1)))
  sum+=a1*(r**(i-1))
  i+=1

print(n,"번째 항까지의 합 : ",sum)
실행 결과 :
7 번째 항의 값 : 3645
1 번째 항 : 5
2 번째 항 : 15
3 번째 항 : 45
4 번째 항 : 135
5 번째 항 : 405
6 번째 항 : 1215
7 번째 항 : 3645
7 번째 항까지의 합 : 5465

시그마(Sigma)

시그마란 수열의 합을 나타내는 기호이다.

예시)
$a = [2,6,18,54,162,486,1458,4374]$
$S_n = {a_1+a_2+a_3+a_4+a_5+a_6+...+a_n}$

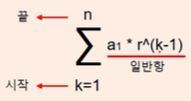
위 그림의 수식대로, 기호에 값을 대입하여 구한다.

시작항부터 끝항까지의 합을 구하는 것으로, 1부터 끝항까지의 합을 구한 뒤, 1부터 시작항까지의 합을 빼면 쉽게 구할 수 있다.

계차수열

두 항의 차이가 또 다른 수열을 이루는 수열이다.
ex)
a = [0,3,8,15,24,35,48,63]
b = a의 항들의 차이 = [3,5,7,9,11,13,15]

한 수열의 차이값들의 목록이 등차수열인 수열이 바로 계차수열이다.

계차 수열을 이용해서 수열 $a_n$ 의 일반항을 구할 수 있다.

a_n = a_1 + (n-1)*d

S_n = n(a_n+a_1)2

b_n의 sigma(1,n-1) = a_n-a_1 = a_n=n^2-1

#예시 코드
ian1 = int(input("a1 입력 : "))#input a1
ian = int(input("an 입력 : "))#input an

ibn1 = int(input("b1 입력 : "))#input b1
ibd = int(input("bn 공차 입력 : "))# input bd

van = 0 #value an
vbn = 0 #value bn

i=1
while i<ian:
  if i==1:
    van=ian1
    vbn=ibn1
    print("an의 {}번째 항의 값 : {}".format(i,van))
    print("bn의 {}번째 항의 값 : {}".format(i,vbn))
    i+=1
    continue

  van = van+vbn
  vbn = vbn+ibd
  print("an의 {}번째 항의 값 : {}".format(i,van))
  print("bn의 {}번째 항의 값 : {}".format(i,vbn))
  i+=1

van = ian**2 + ian + 1
print("an의 {}번째 항의 값 : {}".format(ian,van))
실행 결과 :
a1 입력 : 3
an 입력 : 7
b1 입력 : 4
bn 공차 입력 : 2
an의 1번째 항의 값 : 3
bn의 1번째 항의 값 : 4
an의 2번째 항의 값 : 7
bn의 2번째 항의 값 : 6
an의 3번째 항의 값 : 13
bn의 3번째 항의 값 : 8
an의 4번째 항의 값 : 21
bn의 4번째 항의 값 : 10
an의 5번째 항의 값 : 31
bn의 5번째 항의 값 : 12
an의 6번째 항의 값 : 43
bn의 6번째 항의 값 : 14
an의 7번째 항의 값 : 57

피보나치 수열

피보나치 수열은 굉장히 유명한 수열 알고리즘으로, 계차 수열보단 조금 쉽다.
피보나치 수열은 기본적으로 첫번째 항과 두번째 항이 존재할 때 구현 가능한 수열로, n번째 항은 n-1번째 항과 n-2번째 항의 합이다.
$a_n = a_(n-1)+a_(n-2)$

#피보나치
n = int(input("구하고싶은 n번째 항의 n : "))

a1 = int(input("1번째 항의 값 : "))
a2 = int(input("2번째 항의 값 : "))

i=1
while i<=n-2:
  if i ==1:
    valu = 1
    val1 = a1
    val2 = a2
    valu = a1+a2
    print(i+2,"번째 항의 값 : ",valu)
    i+=1
    continue
 
  val1 = val2
  val2 = valu
  valu = val1+val2
  print(i+2,"번째 항의 값 : ",valu)
  i+=1

실행 결과 :
구하고싶은 n번째 항의 n : 5
1번째 항의 값 : 1
2번째 항의 값 : 1
3 번째 항의 값 : 2
4 번째 항의 값 : 3
5 번째 항의 값 : 5

팩토리얼

n! 로 표기하며, 1부터 양의정수 n까지의 정수를 모두 곱한 것.

n = int(input("양의 정수 n 입력 : "))
def pactorial(n):
  i=1
  temp = 1
  while i<=n:
    temp*=i
    i+=1
  return temp

print(n,"의 팩토리얼 값 : ",pactorial(n))

실행 결과 :
양의 정수 n 입력 : 5
5 의 팩토리얼 값 : 120

군 수열

여러 개의 항을 묶었을 때 규칙성을 가지는 수열
$a = [1,1,2,1,2,3,1,2,3,4,1,2,3,4,5]$
위와 같은 수열일 때, 수들을 묶어서 군이라고 표현한다.
$a = [(1),(1,2),(1,2,3),(1,2,3,4),(1,2,3,4,5)]$

$a_n = a_1+(n-1)*d$
$S_n = n(a_1+a_n)/2$
을 사용하여 군 수열의 n번째 항을 구할 수 있다.

$a_n=n$
$S_n = (n^2 + n)/2$
ex) $50번째 항 구하기 -> (9^2+9)/2 = 45 -> 9군 + 10군의 5번째항 = 5 = 50번째 항$

inputn = int(input("n항 입력 : "))
nCnt=1
n=1
flag = True
while flag:
  for i in range(1,(n+1)):
    print(i,end=" ")
    nCnt +=1
    if nCnt > inputn:
      searchN=i
      flag = False
      break
  print()
  n+=1

print(inputn,"항",searchN)
실행 결과 :
n항 입력 : 50
1
1 2
1 2 3
1 2 3 4
1 2 3 4 5
1 2 3 4 5 6
1 2 3 4 5 6 7
1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 8 9
1 2 3 4 5
50 항 5

순열

n개에서 r개를 택하여 나열하는 경우의 수 중에서 순서를 따져서 순서가 다르면 다른 경우라고 판단.

$nPr = n(n-1)(n-2)(n-3)(n-4).....(n-r+1), 단(0<r<=n)$

순열은 팩토리얼을 이용해서 나타낼 수 있다.

위의 식은 n부터 n-r+1까지의 곱이기 때문에
$n!/(n-r)!$ 로 표현이 가능하다

#nPr

n = int(input("n 입력 : "))
r = int(input("r 입력 : "))
result = 1

for n in range(n,(n-r),-1):
  print("n : ",n)
  result = result * n

print("결과 : "result)
실행 결과 :
n 입력 : 7
r 입력 : 5
n : 7
n : 6
n : 5
n : 4
n : 3
결과 : 2520

조합

순서 상관없이 n개에서 r개를 선택하는 방법

n개중 r개를 고르는 nPr의 값을 구한다면
nCr = nPr/r! = 조합 이다.

n = int(input("n 입력"))
r = int(input("r 입력"))

sumc = 1
sump = 1
for i in range(n-r):
  sumc *= (n-i)
  sumc /=(i+1)
print("조합 : ",sumc)

for j in range(n-r+1):
  sump *= (n-j)
print("순열 : ",sump)

실행 결과 :
n 입력5
r 입력3
조합 : 10.0
순열 : 60

확률

모든 사건에서 특정 사건이 일어날 수 있는 수를 나타낸 것.
ex) 동전의 앞, 뒤 -> 1/2, 1/2

확률과 조합
박스에 꽝이 적힌 종이가 4장, 선물이 적힌 종이가 3장 있을 때 3장을 뽑을 경우의 수.

꽝 : 0, 선물 : 3 -> 1/35
꽝 : 1, 선물 : 2 -> (4C1x3C2)/35 -> 4x3/35 -> 12/35
꽝 : 2, 선물 : 1 -> (5C2x2C1)/35 -> (10x2)/35 -> 20/35
꽝 : 1, 선물 : 2 -> 5ㅊ1/35 -> 5/35

#순열, 조합, 팩토리얼을 n과 r을 입력받아 구하는 함수 구현
def proFun():
  n = int(input("n 입력"))
  r = int(input("r 입력"))
  resultp = 1
  rpact = 1

  for i in range(n,(n-r),-1):
    resultp *= i
  print("resultp : ",resultp)

  for i in range(r,0,-1):
    rpact *= i

  print("rpactorial : ",rpact)

  resultc = int(resultp/rpact)
  print("result c : ",resultc)

  return resultc

event1 = proFun()
print("event1 : ",event1)

event2 = proFun()
print("event2 : ",event2)

event3 = proFun()
print("event3 : ",event3)

probability = (event2 * event3) / event1 * 100
print("probability : %.2f " % probability)
실행 결과 :
n 입력7
r 입력3
resultp : 210
rpactorial : 6
result c : 35
event1 : 35
n 입력4
r 입력2
resultp : 12
rpactorial : 2
result c : 6
event2 : 6
n 입력3
r 입력1
resultp : 3
rpactorial : 1
result c : 3
event3 : 3
probability : 51.43

매생이

이전 포스트

파이썬 기초 2

다음 포스트